Como calcular dominio y rango de una función
Dos conjuntos muy importantes asociados a una función son el dominio y el rango de la misma. En este artículo veremos qué es cada uno y cómo calcularlos analíticamente cuando tenemos la ecuación de la función y también gráficamente.
Índice
Definiciones
En una función general, el campo de existencia o dominio es el conjunto de todos los elementos que admiten imagen. El rango, contradominio, recorrido o conjunto imagen de la función es el conjunto de todas las imágenes de los elementos del dominio. Trabajando con funciones de valores reales podemos mejorar estas definiciones de la siguiente forma:
Si f es una función real:
Dominio de f es el conjunto de todos los valores reales cuya imagen es un número real:
*D_f=\{x∈\mathbb{R}~|~f(x)∈\mathbb{R}\}*
Rango de f es el conjunto de todos los reales que son imagen de algún elemento del dominio:
*R_f=\{y∈\mathbb{R}~|~y=f(x)∧x∈D_f\}*
En algunas bibliografías se presenta el concepto de codominio junto al de rango. Dada una función definida entre los conjuntos A y B, *f: A→B,* llamamos codominio de f al conjunto B. El rango es entonces un subconjunto de B que puede ser o no igual a este. En funciones reales, por convención se toma como codominio al conjunto *\mathbb{R}.*
El trabajo de obtener el dominio consiste en hallar todos los valores que pueden usarse como variable independiente y que arrojan como imagen a un real. Para ello, debemos fijarnos donde se sitúa la variable independiente en la ecuación. Si está en un denominador, debemos asegurarnos de que éste nunca sea cero; si está dentro del argumento de un logaritmo, este debe ser siempre positivo; si se encuentra dentro de una raíz de índice par, el radicando siempre debe ser no negativo, etc.
Calcular el rango no suele ser tan sencillo como en el caso del dominio, incluso muchas veces no es necesario hallarlo. Disponemos de algunas técnicas algebraicas que funcionan en algunos casos, como expresar la relación en función de la variable independiente y realizar un proceso análogo al antes explicado. En otros casos, la naturaleza de la función nos proporciona su rango, como es el caso de las trigonométricas.
Veremos a continuación algunos ejemplos de determinación del dominio y rango a partir de la ecuación de una función. Al final, veremos cómo obtenerlos si tenemos la gráfica.
Dominio y rango de funciones algebraicas
Recordemos que las funciones polinómicas son aquellas de la forma *f(x)=a_0+a_1x+a_2x^2+a_3x^3+…+a_nx^n* donde los *a_0,* *a_1,a_2,...,a_n* son números reales llamados coeficientes. Son polinómicas las funciones lineales, cuadráticas, cúbicas o de cualquier grado. El dominio de una función polinómica es el conjunto de los números reales. El rango de estas funciones en algunos casos es *\mathbb{R}* y en otros no.
Las funciones algebraicas son aquellas que se pueden obtener a partir de funciones polinómicas mediante la realización de operaciones como suma, resta, multiplicación, división o toma de raíces.
Lineales
Dado que estas funciones son un caso particular de las polinómicas, heredan el dominio de ellas. El rango es también amigable en este caso, pues de la forma general *y=mx+b,* si despejamos x, nos queda *x=\frac{y-b}{m}.* Podemos ver que y no tiene limitaciones y puede tomar cualquier valor real (salvo que *m* sea cero, en este caso, solo puede valer b).
El dominio y el rango de una función lineal es el conjunto de los números reales (si m no es cero). Si m es cero, el dominio son los reales y el rango es {b}.
Ejemplos:
*y=2x+1*
*y=3x-1*
*y=x+1*
*y=2x+3*
*y=x*
Por lo dicho antes, todas ellas tienen de dominio y rango al conjunto de los números reales: *D=\mathbb{R}* y *R=\mathbb{R}.* En las gráficas podemos notar cómo se ve esto, las mismas se extienden por el plano cartesiano ocupando todos los valores:
Cuadráticas
El dominio de una función cuadrática es el conjunto de los números reales. Esto es debido a que se trata de una función polinómica, por tanto, hereda su dominio. Entonces, la función cuadrática *f(x)=ax^2+bx+c* tiene por dominio a *D_f=\mathbb{R}.*
El rango de una función cuadrática depende de la expresión, vemos a continuación los casos que pueden ocurrir.
1) Cuando *b=c=0,* ocurre que *f(x)=ax^2*
- Si a es positivo, *R_f=[0, +∞)*
- Si a es negativo, *R_f=(-∞, 0]*
2) Cuando *b=0,~f(x)=ax^2+c*
- Si a es positivo, *R_f=[c, +∞)*
- Si a es negativo, *R_f=(-∞ , c]*
3) Cuando todos los coeficientes son distintos de cero, *f(x)=ax^2+bx+c*
- Si *a* es positivo, *R_f=[k,+∞)*
- Si *a* es negativo, *R_f=(-∞,k]*
donde *k=f(h)* y *h=\dfrac{-b}{2a}*
Ejemplo 1: *f(x)=2x^2*
*D_f=\mathbb{R}*
*R_f=[0,+∞)*
Ejemplo 2: *g(x)=5x^2-2*
*D_g=\mathbb{R}*
*R_g=[-2, +∞)*
Ejemplo 3: *h(x)=-2x^2+3x+1*
*D_h=\mathbb{R}*
*R_h=(-∞, \frac{17}{8}]*
Cúbicas
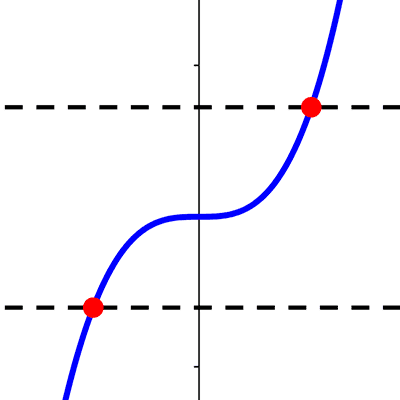
Las funciones cúbicas tienen como dominio y rango al conjunto de los números reales.
Podemos ver una gráfica y notaremos como esta ocupa todos los valores posibles de x e y.
Ejemplos:
*f(x)=2x^3+1~~~D_f=\mathbb{R}~~~R_f=\mathbb{R}*
*g(x)=-7x^3+2x^2-5x-1~~~D_g=\mathbb{R}~~~R_g=\mathbb{R}*
Racionales
Las funciones racionales son aquellas del tipo *f(x)=\frac{p(x)}{q(x)}* donde *p(x)* y *q(x)* son funciones polinómicas. Surge naturalmente que el denominador no puede ser cero, pues dividir por cero es una operación imposible. Entonces:
El dominio de una función racional son todos los números reales excepto aquellos que anulan su denominador.
*D_f=\mathbb{R}-\{x~|~q(x)=0\}*
Ejemplo 1: *f(x)=\dfrac{2x^2+3x-1}{x+1}*
El denominador es *q(x)=x+1.* El dominio ocupará todos los valores reales excepto aquellos que hagan cero a q(x). Es decir: *D_f=\mathbb{R}-\{x/x+1=0\}.* Para conocer los valores excluidos, resolvemos la ecuación *x+1=0,* nos queda *x=-1.* Entonces, *D_f=\mathbb{R}-\{-1\}.*
Ejemplo 2: *g(x)=\dfrac{2x+5}{x^2-4}*
El denominador aquí es *q(x)=x^2-4.* *D_g=\mathbb{R}-\{x/x^2-4=0\}.* Resolvemos la ecuación para conocer los valores excluidos del dominio:
*x^2-4=0*
*x^2=4* sacando raíz cuadrada positiva a ambos miembros:
*\sqrt{x^2}=\sqrt{4}*
*|x|=2*
*x=±2,* entonces *x=2* o *x=-2.* Por lo tanto *D_g=\mathbb{R}-\{-2, 2\}*
Ejemplo 3: *h(x)=\dfrac{1}{x^2+5}*
Identificamos el denominador *q(x)=x^2+5.* Sabemos que *D_h=\mathbb{R}-\{x/x^2+5=0\}.* Resolvemos la ecuación *x^2+5=0→x^2=-5* y nos damos cuenta de que no existen números reales que elevados al cuadrado arrojen un negativo, por lo tanto la ecuación planteada no tiene solución real. Esto se traduce en que no existen valores excluidos del dominio, resultando que *D_h=\mathbb{R}.*
Calcular el rango de una función racional no suele ser tan sencillo porque no podemos predecir con exactitud qué ocurrirá con la gráfica. Sin embargo, tenemos algunos casos especiales en los que sí es posible determinar el rango.
Por ejemplo, las funciones racionales del tipo *f(x)=\dfrac{ax+b}{cx+d}* (llamadas funciones homográficas) donde numerador y denominador son funciones lineales, tienen por rango a todos los reales exceptuando el número *\frac{a}{c}.* $$R_f=\mathbb{R}-\left\{\frac{a}{c}\right\}$$
Ejemplo 1: *f(x)=\dfrac{-2x+3}{x-1}*
El dominio lo obtenemos haciendo el proceso antes explicado, *D_f=\mathbb{R}-\{x/x-1=0\}=\mathbb{R}-\{1\}.* Para el rango identificamos los coeficientes principales de los polinomios del numerador y denominador, ellos son los números que multiplican a las x. *a=-2,* coeficiente principal del numerador, *c=1* el del denominador. El rango entonces es:
*R_f=\mathbb{R}-\left\{\dfrac{a}{c}\right\}=\mathbb{R}-\left\{\dfrac{-2}{1}\right\}=\mathbb{R}-\{-2\}*
Ejemplo 2: *g(x)=\dfrac{4}{-x+5}*
Obtenemos el dominio como *D_g=\mathbb{R}-\{x/-x+5=0\}=\mathbb{R}-\{5\}.* Identificamos que en el numerador el coeficiente principal es cero, porque no aparece x, entonces *a=0.* En el denominador, *c=-1.* Entonces el rango es:
*R_g=\mathbb{R}-\left\{\dfrac{a}{c}\right\}=\mathbb{R}-\left\{\dfrac{0}{-1}\right\}=\mathbb{R}-\{0\}*
Irracionales
En las funciones con raíces debemos tener en cuenta que, si esta raíz tiene índice par, el radicando no puede ser negativo, porque la raíz de índice par de un número negativo no es un número real. En cambio, en las raíces de índice impar, no hay restricciones hacia los radicandos negativos. Entonces:
El dominio de una función con raíz de índice par son todos los reales excepto los que hacen negativo al radicando. El dominio de una función con raíz de índice impar son todos los números reales.
El rango en estas funciones sigue una lógica parecida al dominio. Las raíces de índice par tienen por rango a los reales no negativos *[0,+∞)* y las de índice impar a todos los reales *\mathbb{R}.*
Ejemplo 1: *f(x)=\sqrt[2]{2x-5}*
El radicando es 2x-5, debemos asegurarnos de que nunca sea negativo porque la raíz es de índice par (2). Entonces *D_f=\{x/2x-5≥0\}*
Resolvemos la inecuación planteada *2x-5≥0→x≥\dfrac{5}{2}.*
Entonces *D_f=\left\{x~|~x≥\dfrac{5}{2}\right\}=[\frac{5}{2} ,1).* El rango, por el índice par, es *R_f=[0, +∞).*
Ejemplo 2: *g(x)=\sqrt[3]{-x+2}*
Como se trata de una raíz de índice impar 3, no importa si el radicando *-x+2* se hace negativo. El dominio y el rango siguen siendo *\mathbb{R}.* Entonces *D_g=\mathbb{R},* *R_g=\mathbb{R}.*
Dominio y rango de funciones trascendentes
Recopilaremos a continuación el dominio y el rango de las funciones trascendentes: exponenciales, logarítmicas, trigonométricas e hiperbólicas.
Exponenciales
Las funciones exponenciales son las del tipo *f(x)=a^x* donde a es real positivo distinto de 1. La x puede tomar cualquier valor, con lo cual el dominio de la función es *\mathbb{R}.* El rango son todos los reales positivos, ya que no existe valor de x que haga a una expresión de ese tipo negativa o igual a cero (ni *x=0,* ya que ocurre que *a^0=1*). Entonces:
El dominio de una función exponencial es el conjunto de los números reales y su rango son todos los reales positivos.
Dado *f(x)=a^x,~a>0,~a≠1:*
*D_f=\mathbb{R}*
*R_f=(0, +∞)*
Logarítmicas
Las funciones logarítmicas son aquellas del tipo *f(x)=\log_a x* donde a es positivo y *a≠1*. La restricción que tienen es que el argumento siempre debe ser positivo. Como rango puede tomar todos los números reales.
El domino de una función logarítmica son los números reales que hacen positivo a su argumento. Su rango son todos los reales.
Dado *f(x)=\log_a x,~a>0,~a≠1:*
*D_f=(0, +∞)*
*R_f=\mathbb{R}*
Trigonométricas
Hiperbólicas
Dominios y rangos restringidos
Cuando disponemos de la ecuación que define a una función, solemos considerar como dominio al conjunto máximo de valores que puede tomar la variable independiente, esto es conocido como el dominio natural el cual venimos tratando hasta este punto. Si la situación que trabajamos requiere que la variable independiente tome solo un determinado intervalo de valores, debemos establecerlo. En tal caso lo que hacemos es formar un dominio restringido. Restringir el dominio suele también restringir el rango.
Por ejemplo, sea la función *A(x)=πx^2.* Reconocemos rápidamente que se trata de una función polinómica cuadrática, con lo cual su gráfica es una parábola. Ahora bien, esta función podemos interpretarla como el área de un círculo de radio x. En este contexto, solo nos interesan los valores no negativos de x, pues un radio no puede tomar valores negativos. El razonamiento nos lleva a una restricción del dominio solo para x≥0, y la gráfica pasa a ser la mitad de una parábola:
El dominio natural de la función *A(x)=πx^2* es *\mathbb{R},* pero mediante nuestra delimitación, el dominio pasa a ser *[0,+∞).* El rango se mantiene sin variación.
Ahora, supongamos que tenemos la misma función, pero solo no interesa calcular áreas de círculos con radios mayores a 1, excluyendo a ese número. Entonces, el dominio pasa a ser *(1,+∞).* El rango ahora sí se modifica, y en lugar de ser *[0, +∞)* ahora es *(π,+∞).* Véase la gráfica:
Hallar dominio y rango gráficamente
Cuando tenemos acceso a la regla de definición la ecuación de la función, podemos obtener el dominio analíticamente y en algunos casos también el rango, esto es lo que hicimos hasta ahora. Pero, si solo disponemos de una gráfica, es necesario apelar a nuestros conocimientos para determinar ambos conjuntos. El dominio lo sacamos mirando la porción ocupada sobre el eje horizontal y el rango por la porción sobre el eje vertical.

Para hallar dominio, miramos solo el eje horizontal eje x. Para hallar el rango, nos fijamos solo en el eje vertical eje y.
Ejemplo 1:
Observamos un trozo de línea recta. Con ayuda de segmentos perpendiculares al eje horizontal y vertical, logramos encontrar los puntos por los cuales se extiende la gráfica. Mirando el eje x, el dominio abarca todo el intervalo entre los puntos lilas, y el rango el intervalo entre los puntos azules. Con esta ayuda visual, logramos ver que la función f tiene:
*D_f=[-3,3]*
*R_f=[-4,4]*
Ejemplo 2:
Una gráfica más complicada que la anterior, pero utilizando el mismo recurso de los segmentos perpendiculares logramos obtener los intervalos que nos interesan:
*D_f=[-3; 1,5]*
*R_f=[1,4]*
Ejemplo 3:
Aquí observamos que hay un pequeño hueco en la gráfica, esto nos indica que el punto no pertenece a la misma, con lo cual lo excluiremos del dominio y del rango. Realizamos el procedimiento de los ejemplos anteriores y obtenemos que:
*D_f=[-1,1) \cup (1,2]*
*R_f=[1; 1,5) \cup (1,5 ;3]*
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.












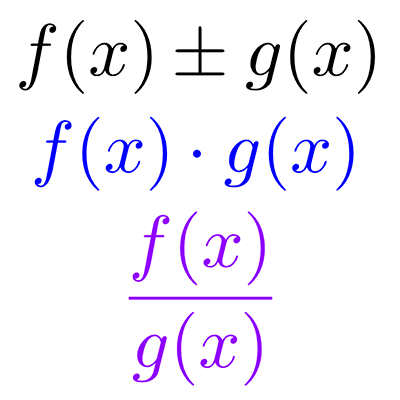
Deja una respuesta