
Logaritmos
En este artículo explicamos qué es el logaritmo, para qué se utiliza, qué tipos existen, cómo se calcula y cuáles son sus propiedades importantes.
Índice
¿Qué es un logaritmo?
En matemáticas, un logaritmo es el exponente al que se debe elevar un número real positivo, llamado base, para que resulte igual a un determinado número, llamado argumento.
Si tenemos una ecuación del tipo *x^2=16,* podemos resolverla con cualquiera de los métodos conocidos y llegar a que *x=±4.* Sin embargo, cuando tenemos una expresión como *4^x=16,* ya no es posible utilizar un método conocido para hallar el valor de *x* que hace verdadera esa expresión. Por tanteo podemos determinar que el valor de *x* es *2,* pero con una ecuación más complicada tampoco es factible usar este método.
Para solventar estas situaciones es que surge el concepto de logaritmo, que consiste en encontrar el exponente al que hay que elevar una base para obtener un número dado.
Dada una ecuación *a^x=b,* donde *a* y *b* son números conocidos, el valor al que hay que elevar *a* para obtener *b* es el logaritmo en base *a* de *b*. Simbólicamente:
*\log_a b=x*
Se lee “el logaritmo en base a de b es igual a x”. Las partes del logaritmo son: base (el número a), argumento (b) y logaritmo (x), este último también es llamado resultado o valor del logaritmo. Por ejemplo, *\log_5(125)* es el número al que hay que elevar *5* para que el resultado sea *125;* *5* es la base y *125* es el argumento, el valor del logaritmo es *3,* porque *5^3=125.*
Ahora, *a* y *b* no pueden ser números cualesquiera, tienen ciertas restricciones. De otro modo podemos caer en contradicciones operativas. La base *a* tiene que ser positiva y distinta de *1.* El argumento *b* debe ser un número positivo.
La primera restricción se debe *a* que si la base fuera un número negativo, podríamos intentar aplicar logaritmos para resolver una ecuación del tipo *(-2)^x=8,* la cual no tiene solución en los números reales. Tampoco puede ser 1, pues una expresión del tipo *1^x=18* no tiene solución, porque la unidad elevada a cualquier exponente no cambia.
La segunda restricción es causada en parte por la primera: teniendo una base positiva, no es posible encontrar un exponente que haga que el resultado sea negativo o cero. Por ejemplo, la ecuación *2^x=-50* no tiene solución con números reales.
Formalizamos todo este razonamiento con la definición de logaritmo.
Definición: El logaritmo en base *a* dada (positiva y distinta de 1) de un número positivo *b* es el exponente al que hay que elevar *a* para que resulte igual a *b.* En símbolos:
*\log_a{b}=x* si y sólo si *a^x=b*
Las relaciones *a^x=b* y *x=\log_a{b}* son equivalentes. *a^x=b* es llamada forma exponencial; *x=\log_a{b}* es la forma logarítmica. Como consecuencia, a cada propiedad de la potenciación le corresponde una propiedad de la logaritmación.
El resultado de un logaritmo puede ser positivo, negativo o cero. Veamos algunos ejemplos:
¿A qué número hay que elevar 2 para obtener 32? La pregunta equivale a la expresión *\log_2{32}.* La respuesta es *5,* pues *2^5=32.* Entonces *\log_2{32}=5*
¿A qué exponente se debe elevar 3 para obtener *\dfrac{1}{9}*? Esto es igual a *\log_3{\dfrac{1}{9}}.* El resultado es *-2,* pues *3^{-2}=\dfrac{1}{3^2}=\dfrac{1}{9}.* Entonces *\log_3{\dfrac{1}{9}}=-2*
¿Cuál es el valor al que se debe elevar 5 para obtener 1? O sea, *\log_5{1}.* La respuesta es cero, pues todo número positivo (o negativo) elevado a cero es igual a *1.* Entonces *\log_5{1}=0*
Existen casos particulares donde el resultado del logaritmo es fácil de hallar, uno de ellos lo vimos en el ejemplo anterior:
- El logaritmo en cualquier base de 1 es igual a cero. *\log_a{1}=0* (pues *a^0=1*)
- El logaritmo de la base es igual a 1: *\log_a{a}=1* (pues *a^1=a*)
Podemos ver que el logaritmo es positivo cuando el argumento es mayor que 1; es negativo cuando el argumento está entre 0 y 1 y es cero cuando el argumento es 1. No existe el logaritmo de cero porque la base no puede ser cero.
Más ejemplos:
*\log_3{9}=2* porque *3^2=9*
*\log_{10}{1000}=3* porque *10^3=1000*
*\log_2{\dfrac{1}{4}}=-2* porque *2^{-2}=\dfrac{1}{4}*
*\log_5{25}=2* porque *5^2=25*
*\log_5{0,04}=\log_5{\dfrac{1}{25}}=-2* porque *5^{-2}=\dfrac{1}{25}=0,04*
*\log_6{216}=3* porque *6^3=126*
*\log_2{64}=6* porque *2^6=64*
Años atrás, para determinar valores de logaritmos se utilizaban tablas de logaritmos que figuraban al final de los libros de matemáticas. Actualmente cualquier calculadora científica permite calcular logaritmos.
¿Para qué se utilizan los logaritmos?
Los logaritmos tienen diversas aplicaciones en matemáticas, ciencias naturales, ingeniería y muchas otras áreas. Algunas de sus principales utilidades de los son:
- Simplificación de cálculos: los logaritmos permiten convertir operaciones de potencia en operaciones de multiplicación, lo que facilita el cálculo de números grandes o complicados.
- Resolución de ecuaciones exponenciales: cuando una variable se encuentra en un exponente, el logaritmo puede utilizarse para despejarla y resolver la ecuación.
- Escalas logarítmicas: en ciertas situaciones, como en la medición de magnitudes como el pH, el sonido (decibelios), la intensidad sísmica (escala de Richter) o la luminosidad de las estrellas (magnitud aparente), se utilizan escalas logarítmicas para representar mejor la relación entre los valores.
- Análisis de crecimiento: los logaritmos pueden utilizarse para analizar y comparar tasas de crecimiento, especialmente en campos como la economía y la demografía.
Tipos de logaritmos
Existen logaritmos que tienen nombres propios por la base que utilizan. Los más comunes son:
- Logaritmos decimales (log): tienen como base el número 10. Se suelen simbolizar como log sin escribir la base: *\log{b}* es equivalente a *\log_{10}{b}.* Estos logaritmos también son llamados vulgares, comunes o de Briggs.
- Logaritmos naturales (ln): tienen como base al número irracional *e≈2,718281…* Se simbolizan con las iniciales de su nombre sin escribir la base: *\ln{b}* equivale a *\log_e{b}.* Estos logaritmos a veces son informalmente llamados logaritmos neperianos.
- Logaritmos binarios: tienen como base al número 2. No tienen una notación especial: *\log_2{b}.* Son utilizados principalmente en informática.
Leyes de los logaritmos
Los logaritmos tienen una serie de propiedades que facilitan su manejo y cálculo. Algunas de estas se derivan rápidamente de la potenciación, pues como vimos antes los logaritmos son exponentes.
- El logaritmo de la base es igual a 1. *\log_a{a}=1*
- El logaritmo de 1 en cualquier base es 0. *\log_a{1}=0*
- El logaritmo de un producto es igual a la suma de logaritmos de los factores: *\log_a(b\cdot c)=\log_a{b}+\log_a{c}*
- El logaritmo de un cociente es igual a la resta de logaritmos: *\log_a\left(\dfrac{b}{c}\right)=\log_a{b}-\log_a{c}*
- El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base. *\log_a(b^n)=n\cdot \log_a{b}*
- Como el logaritmo en base *a* de *b* es el número al que se debe elevar *a* para obtener *b,* entonces: *a^{\log_a{b}}=b*
Cambio de base
Dijimos antes que para calcular logaritmos se pueden usar calculadoras. Ahora bien, estas solo permiten calcular logaritmos naturales o decimales. ¿Qué pasa entonces si queremos usar otras bases? La siguiente propiedad nos permite convertir un logaritmo de una base en un logaritmo de otra base.
*\log_a{b}=\dfrac{\log_k{b}}{\log_k{a}}* donde *k* es la nueva base
Para calcular, por ejemplo, un logaritmo binario, podemos transformarlo en decimal o natural usando esta ley.
*\log_2{b}=\dfrac{\log{b}}{\log{2}}*
*\log_2{b}=\dfrac{\ln{b}}{\ln{2}}*
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Leithold, L. (1994). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.











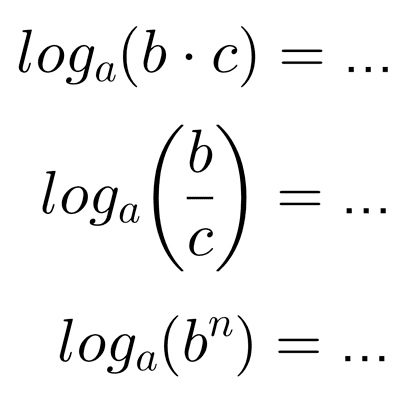


Última actualización del contenido: 23/06/2024
2 Comentarios
Deja una respuesta

en un ejemplo se equivocaron, pero información muy clara y precisa, gracias