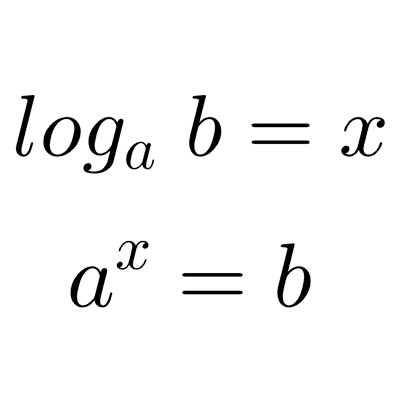
Fórmulas de logaritmos
A continuación se expresan todas las fórmulas útiles a la hora de trabajar con logaritmos.
Índice
Definición de logaritmo
El logaritmo es el exponente (x) al que se debe elevar la base (b) para que el resultado sea igual al argumento (a).
logb (a)=x si y sólo si bx=a
Propiedades de los logaritmos
- Logaritmo de una multiplicación: logb(xy)=logb(x)+logb(y)
- Logaritmo de una división: logb(x/y)=logb(x)-logb(y)
- Logaritmo de una potencia: logb(xn)=n⋅logb(x)
- Logaritmo de la base: logb(b)=1
- Logaritmo de una potencia de la base: logb(bn)=n
- Logaritmo de la unidad: logb(1)=0
- Logaritmo como exponente de la base: blogb(x)=x
Fórmulas de cambio de base
- General: *\log_b(a)=\dfrac{\log_k(a)}{\log_k(b)}*
- Logaritmo natural a decimal: *\ln(a)=\dfrac{\log(a)}{\log(e)}*
- Logaritmo decimal a natural: *\log(a)=\dfrac{\ln(a)}{\ln(10)}*
Formulario en PDF
Puedes descargar el formulario completo pulsando el siguiente botón:
