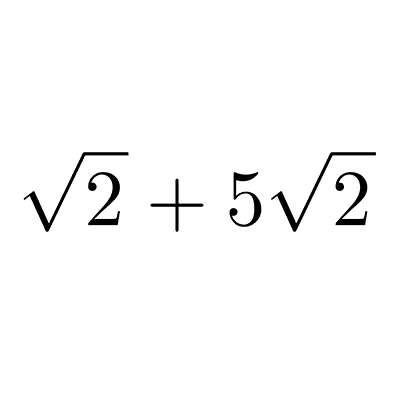
Números irracionales
En este artículo explicamos el conjunto de números irracionales. Abordaremos su concepto, definición, simbología, interpretación en la recta numérica, ejemplos, operaciones que pueden realizarse y las propiedades que estos números cumplen.
Índice
¿Qué son los números irracionales?
Los números irracionales son números reales que no pueden expresarse en forma de fracción, es decir, no se pueden escribir como un cociente de números enteros. En otros términos, los números irracionales no pueden escribirse de la forma a/b donde a y b son enteros y b≠0. Ejemplos de números irracionales son: π, ϕ, e, √2, √3, √5, ∛2, π2, -∛5, -2e.
La palabra "irracional" proviene del latín "irrationalis", que significa "sin razón" o "sin proporción". La principal característica de los números irracionales es que su expresión decimal es infinita y no sigue ningún patrón. Esto los diferencia de los números racionales, los cuales en su forma decimal tienen una cantidad finita de cifras o una cantidad infinita donde un grupo de cifras se repite constantemente.
¿Por qué surgen los números irracionales?
Los números irracionales surgen como una consecuencia natural de la necesidad de expresar cantidades que no pueden representarse como fracciones. Por ejemplo, para expresar las soluciones de la ecuación x2=2 no pueden usarse números racionales, pues ningún racional elevado al cuadrado da como resultado 2. La solución positiva de esta ecuación es la llamada raíz cuadrada de 2, que podemos aproximar así:
*\sqrt{2}=1,41421356237309…*
Podríamos calcular más cifras decimales, pero nunca terminaríamos. Además, no hay cifras que se repitan periódicamente. Esto nos da la pauta de la raíz cuadrada de 2 es un número irracional.
La existencia de números irracionales fue un descubrimiento sorprendente en la historia de las matemáticas, ya que contradecía la concepción antigua de que todos los números podían expresarse como fracciones.
Los números irracionales tienen una importante presencia en geometría, especialmente en la medida de longitudes, áreas y volúmenes. Por ejemplo, el valor de π (un irracional muy conocido) aparece en fórmulas para calcular la circunferencia y el área de un círculo.
Conjunto de los números irracionales
Al conjunto de todos los números que no se pueden escribir como fracción se le llama conjunto de los números irracionales, y se simboliza con la letra I.
*I=\{x |* x no se puede escribir como a/b donde a y b son enteros y b≠0 *\}*
o también, *I=\{x |* la representación decimal de x no es exacta ni periódica *\}*
Todos los números irracionales son números reales, pero no todos los reales son irracionales. Si un número es irracional, entonces no puede ser natural, entero ni, evidentemente, racional, pero sí es un número real.
El conjunto de números irracionales es infinito y no contable, lo que significa que hay una cantidad infinita de números irracionales entre cualquier par de números reales.
Descarga gratis la hoja de ejercicios de conjuntos numéricos para practicar.
Ejemplos de números irracionales
Algunos irracionales que podemos mencionar son:
- Las raíces de números naturales cuyos resultados no son naturales. Ejemplos: *\sqrt{5},\sqrt{11}, \sqrt{17}, \sqrt{26},...*
- Las raíces de números enteros cuyos resultados no son enteros. Ejemplos: *\sqrt[3]{3},\sqrt[7]{-21},\sqrt[5]{-14},...*
- Las raíces de números racionales cuyos resultados no son racionales. *\sqrt[2]{\dfrac{1}{2}}, \sqrt[3]{-\dfrac{1}{3}}, \sqrt{0,75},...*
- Números obtenidos combinando infinitas cifras decimales sin periodicidad. Por ejemplo: *0,010010001..., 0,020020002…*
- Números que surgen de la geometría u otras ramas de la matemática: *\pi, \phi, e, e^2, \pi+1,* estos números los trataremos más adelante.
Para obtener un número irracional, es suficiente escribir un número cuyas cifras decimales sean infinitas y no presenten periodicidad. Por ejemplo: 3,515511555111...
Se puede demostrar la irracionabilidad de ciertos números usando métodos como el de reducción al absurdo o argumentos geométricos. En una calculadora científica se pueden aproximar los valores de números irracionales.
Importante: todo número real a se puede escribir de la forma a/1. Sin embargo, que esta representación sea posible no significa que el número sea racional. √2 / 1 es un número irracional, aunque parezca que se puede escribir como fracción. Recuerde que para que sea una fracción se requiere que el numerador y el denominador sean ambos números enteros.
Clasificación de los números irracionales
Los números irracionales se dividen en dos tipos: los irracionales algebraicos y los irracionales trascendentes.
Irracionales algebraicos
Los números irracionales algebraicos son aquellos que son soluciones de ecuaciones polinómicas con coeficientes enteros. O sea, son soluciones a una ecuación de la forma *a_n x^n+a_{n-1} x^{n-1}+...+a_1 x+a_0=0,* donde *a_n, a_{n-1},...,a_1,a_0* son números enteros y n es un número natural. Los irracionales algebraicos pueden expresarse de manera algebraica en términos de sumas, restas, multiplicaciones, divisiones y raíces de números enteros.
Todas las raíces no exactas de cualquier índice son irracionales algebraicos. Por ejemplo: *\sqrt{2}, \sqrt{3}, \sqrt[3]{7}, -\sqrt[4]{13}, etc.* La raíz cuadrada de 2 es solución de la ecuación *x^2-2=0,* la raíz cúbica de 3 es solución de *x^3-3=0,* y así se puede seguir con cualquier expresión radical no exacta. El número de oro *\phi* es un irracional algebraico, pues se puede escribir como *\phi=\dfrac{1+\sqrt{5}}{2}*
Irracionales trascendentes
Los números irracionales trascendentes son aquellos que no son soluciones de ecuaciones polinómicas con coeficientes enteros, lo que significa que no pueden expresarse de manera algebraica en términos de sumas, restas, multiplicaciones, divisiones y raíces de números enteros. Algunos ejemplos conocidos de números irracionales trascendentes son π y e.
Números irracionales famosos
Existen tres números irracionales muy conocidos en matemáticas y otras ciencias, ellos son: π (pi), ϕ (fi) y e (o número de Euler).
Número π
Pi es un número irracional fundamental en matemáticas que representa la relación entre la circunferencia de un círculo y su diámetro. Su valor aproximado es:
*\pi=3,14159265...*
Desde la antigüedad, ha fascinado a matemáticos y científicos, y su estudio continúa siendo relevante en diversas áreas, incluyendo la geometría, la física y la informática.
Dado un círculo con perímetro (o circunferencia) C y diámetro d, se cumple la siguiente relación:
*\dfrac{C}{d}=\pi*
Es decir, el diámetro de un círculo entra *\pi* veces en el perímetro del mismo.
Número ϕ
El número fi, también conocido como el número de oro, número áureo o la proporción áurea, es un número irracional cuyo valor aproximado es:
*\phi=1,6180339887...*
Este número es la solución positiva a la ecuación cuadrática *x^2=x+1,* con lo cual se puede escribir como:
*\phi=\dfrac{1+\sqrt{5}}{2}*
El número fi es notable por su presencia en la naturaleza y el arte, ya que se encuentra en la disposición de pétalos de muchas flores, en la arquitectura de edificios famosos como la Parthenon, y en otras manifestaciones estéticas. Es un símbolo de armonía y belleza, y su estudio ha sido central en campos como la geometría, el arte y la teoría de números.
Número e
El número e, también llamado número de Euler, es otro irracional fundamental en matemáticas. Es la base de los logaritmos naturales y surge en diversas áreas como la probabilidad, la estadística, el cálculo y la física.
*e=2,71828182845904...*
El número e también puede definirse como el valor al que tiende la expresión *\left(1+\dfrac{1}{x}\right)^x* cuando *x* se hace muy grande. Simbólicamente, esto se expresa como:
*e=\lim_{x\to \infty}\left(1+\dfrac{1}{x}\right)^x*
El número de Euler es también es la base de la función exponencial natural *e^x*, la cual tiene un papel crucial en el estudio de fenómenos que exhiben un crecimiento exponencial, como el interés compuesto, el crecimiento de poblaciones y otras aplicaciones en ciencias naturales y sociales.
Representación en la recta numérica
Los números racionales no son capaces de completar la recta numérica sin dejar huecos. Esos espacios sobrantes son completados por los números irracionales. Entre dos números racionales cualesquiera existen infinitos números irracionales.
Operaciones con números irracionales
Las operaciones que pueden realizarse entre números irracionales son las mismas que pueden hacerse con cualquier número real. Estas operaciones incluyen suma, resta, multiplicación y división. Además, se siguen cumpliendo las propiedades de estas operaciones:
- Asociatividad: el orden en que se agrupan los números en la suma y la multiplicación no afecta al resultado final.
- Conmutatividad: el orden en que se suman o multiplican los números no afecta al resultado final.
- Elemento neutro: en la suma, el elemento neutro es 0, lo que significa que sumado a cualquier número no altera el valor original. Ejemplo: √5+0=√5. En la multiplicación, el elemento neutro es 1, con lo cual ocurre lo análogo a la suma, por ejemplo, π ⋅ 1=π.
- Elemento inverso: La suma de un número irracional con su opuesto (el negativo del número) es igual a cero, por ejemplo, ∛6+(-∛6)=0. La multiplicación de un irracional a por su inverso 1/a es igual a uno, por ejemplo, √3 ⋅ 1/√3 = 1.
- Distributividad: esta propiedad establece que la multiplicación se distribuye sobre la suma. Por ejemplo: e (π+√2) = eπ + e√2.
Habitualmente, cuando se habla de operar números irracionales nos referimos a trabajar con expresiones radicales, es decir, aquellas que son raíces cuadradas, cúbicas u otras raíces de números. En estos artículos puedes aprender cómo realizar cada una de las operaciones:
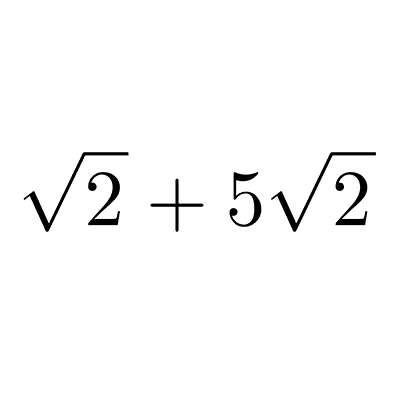
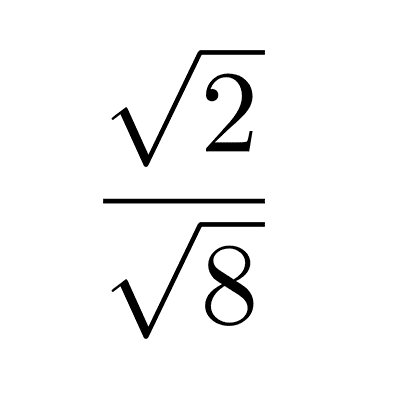
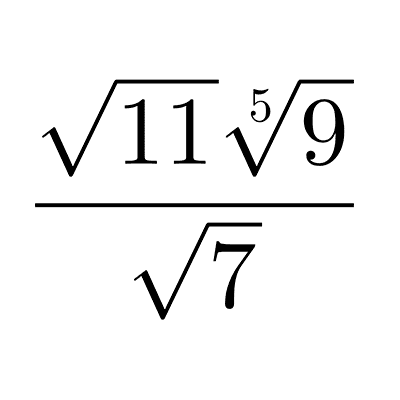
Propiedades de los números irracionales
Las operaciones con irracionales siguen también las siguientes propiedades.
- La suma o producto de dos números irracionales puede arrojar un resultado racional o irracional.
- La suma o resta de un racional con un irracional, da como resultado un irracional.
- El producto entre un racional no nulo y un irracional da como resultado un irracional.
- El cociente entre un racional no nulo y un irracional, da como resultado un irracional.
- El inverso multiplicativo de un irracional es otro irracional.
Preguntas frecuentes
¿Cuáles son los 3 números irracionales más famosos?
Los tres irracionales especiales que tienen nombres propios son:
π (pi): la razón entre el perímetro y el diámetro de una circunferenica.
e: el número de Euler, la base de los logaritmos naturales.
φ (fi): el número de oro, una proporción observada en la naturaleza.
¿Cuántas cifras decimales tiene un número irracional?
Un número irracional tiene infinitas cifras decimales que no siguen ningún patrón.
¿Cómo saber si una raíz es irracional?
Si una raíz no arroja un número entero o con una cantidad finita o periódica de decimales, entonces es un número irracional.
¿Cuál es el símbolo de los números irracionales?
El conjunto de los números irracionales se simboliza con la letra I.
