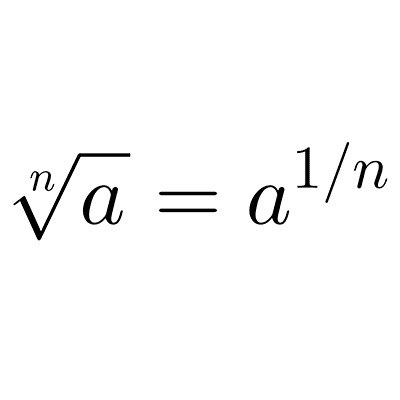
Suma y resta de radicales

En este artículo explicamos cómo resolver la suma y resta de radicales, es decir, de expresiones con raíces cuadradas, cúbicas o de cualquier índice. Veremos el paso a paso con ejercicios resueltos.

Suma y resta de radicales semejantes (iguales)

Antes de comenzar a explicar la adicción y sustracción de radicales es importante recordar conceptos importantes sobre estos.

Dos radicales son semejantes si tienen el mismo índice y el mismo radicando. A simple vista, se ven iguales. 

Por ejemplo, en la expresión *2\sqrt{8}+5\sqrt{8}* los radicales que aparecen son semejantes. Se llama coeficiente al número que multiplica al radical. En el ejemplo, los coeficientes son *2* y *5.* 

En la expresión *8\sqrt{6}-2\sqrt[3]{6}* no hay radicales semejantes, pues aunque tengan el mismo radicando (lo que aparece dentro de la raíz), los índices son diferentes.

Si tenemos una suma de radicales y estos son iguales, por ejemplo en *2\sqrt{8}+5\sqrt{8},* podemos pensar en extraer como factor común al radical. De este modo, *\sqrt{8}* es el factor común y la expresión equivalente es: *2\sqrt{8}+5\sqrt{8}=(2+5)\sqrt{8}.* Generalizando este razonamiento encontramos una fórmula para sumar raíces iguales.

Ejemplo 1

*2\sqrt{3}+5\sqrt{3}*

En este caso, tenemos la suma de raíces cuadradas cuyos radicandos son iguales. Siguiendo la fórmula, sumamos los coeficientes y mantenemos la misma raíz:

*2\sqrt{3}+5\sqrt{3}=(2+5)\sqrt{3}=7\sqrt{3}*

Una forma sencilla de entenderlo es: si tenemos dos veces algo y cinco veces ese mismo algo, en total tenemos siete veces ese algo. 

Ejemplo 2

*6\sqrt{7}-4\sqrt{7}+\sqrt[3]{7}*

En la expresión identificamos que aparece dos veces la raíz cuadrada de siete y una vez la raíz cúbica de siete. Aunque esta última raíz tenga el mismo radicando que las otras, no es suficiente para ser semejante a ellas, porque los índices son diferentes. En este caso, se suman los radicales que sí son semejantes y el otro se deja expresado tal cual.

*6\sqrt{7}-4\sqrt{7}+\sqrt[3]{7}=(6-4)\sqrt{7}+\sqrt[3]{7}=2\sqrt{7}+\sqrt[3]{7}*

Ejemplo 3

*\sqrt[3]{6}-3\sqrt[4]{5}+7\sqrt[3]{6}+8\sqrt[4]{5}*

En esta expresión podemos identificar dos pares de radicales semejantes: las raíces cúbicas de seis y las raíces cuartas de cinco. Para resolver esta operación sumamos cada radical con su semejante.

*\sqrt[3]{6}-3\sqrt[4]{5}+7\sqrt[3]{6}+8\sqrt[4]{5}=(1+7)\sqrt[3]{6}+(-3+8)\sqrt[4]{5}*

*=8\sqrt[3]{6}+5\sqrt[4]{5}*

Ejemplo 4

Los coeficientes de los radicales pueden ser fracciones, en tal caso al sumar o restar se siguen las reglas de estos números.

*\dfrac{7}{4}\sqrt{11}+\dfrac{6\sqrt{11}}{5}=\left(\dfrac{7}{4}+\dfrac{6}{5}\right)\sqrt{11}*

*=\dfrac{59}{20}\sqrt{11}*

Ejemplo 5

Si aparecen variables (letras) en el radicando o en los coeficientes, se sigue operando de igual forma que hasta ahora. Aquí vemos dos casos:

*(x+1)\sqrt{3}+26\sqrt{3}=(x+1+26)\sqrt{3}=(x+27)\sqrt{3}*

*a\sqrt{x+7}+2a\sqrt{x+7}=(a+2a)\sqrt{x+7}=3a\sqrt{x+7}*

Suma y resta de radicales no semejantes (distintos)

A veces, dos radicales que no son semejantes pueden serlo realizando una simplificación adecuada. Por ejemplo, a simple vista en la operación *9\sqrt{3}+\sqrt{75}* no hay radicales semejantes, pero se puede reescribir el segundo término siguiendo estos pasos:

1. Factorizar el radicando: *75=5^2\cdot 3*
2. Escribirlo dentro del símbolo radical y simplificar mediante la propiedad de las raíces: *\sqrt{75}=\sqrt{5^2\cdot 3}=\sqrt{5^2}\sqrt{3}=5\sqrt{3}*
3. Reemplazar en la expresión original: *9\sqrt{3}+{\color{green}5\sqrt{3}},* la cual ahora tiene radicales semejantes que pueden operarse como se vio anteriormente, dando por resultado *14\sqrt{3}*

Para sumar o restar radicales no semejantes, se intentan simplificar para que lo sean. Si esto no es posible, se deja expresada la suma o resta sin modificación.

Hay propiedades útiles para tener en cuenta en las simplificaciones, las vemos a continuación.

Por ejemplo, multiplicando el exponente y el índice por 2 en *\sqrt{2}* se obtiene *\sqrt[2\cdot 2]{2^2}=\sqrt[4]{4},* que es equivalente a la raíz cuadrada original.

A veces, una forma más cómoda de trabajar con radicales es pensarlos como números con exponentes fraccionarios, de acuerdo con la siguiente propiedad.

Entonces, por ejemplo, *\sqrt{2}* es lo mismo que escribir *2^\frac{1}{2}.* Al pensar en exponentes, se aplican todas sus leyes. Así, la propiedad anterior se entiende como multiplicar el exponente fraccionario por una fracción que equivale a 1.

En nuestro ejemplo, *\sqrt{2}* era igual a *\sqrt[4]{4}.* Si lo escribimos en forma de exponente, vemos por qué ocurre esto:

*\sqrt[4]{4}=\sqrt[4]{2^2}=2^\frac{2}{4}=2^\frac{1}{2}=\sqrt{2}*

Del mismo modo, se puede llegar desde *\sqrt{2}* hasta *\sqrt[4]{4}* multiplicando el exponente por *\dfrac{2}{2},* que es igual que multiplicar por 1, entonces el valor no cambia.

*\sqrt{2}=2^\frac{1}{2}=2^{\frac{1}{2}\cdot {\color{green}\frac{2}{2}}}=2^\frac{2}{4}=\sqrt[4]{2^2}=\sqrt[4]{4}*

Conocer estas propiedades nos servirá a la hora de simplificar expresiones para lograr radicales semejantes. Veremos a continuación tres casos que pueden darse cuando buscamos sumar o restar radicales que no son semejantes a simple vista.

Caso 1: Radicales con igual índice y diferente radicando

Si las raíces coinciden en índice pero no en radicando, lo principal será descomponer este último en factores primos y dejando dentro de la raíz solo aquellos que resulten convenientes.

Ejemplo 1: *6\sqrt{63}+4\sqrt{7}*

El *63* se puede factorizar como *63=3^2\cdot 7.* La raíz quedará como *\sqrt{63}=\sqrt{3^2 \cdot 7}=\sqrt{3^2}\sqrt{7}=3\sqrt{7}*

Entonces, reemplazando en la expresión original:

*6{\color{green}\sqrt{63}}+4\sqrt{7}=6\cdot {\color{green}3\sqrt{7}}+4\sqrt{7}*

*=18\sqrt{7}+4\sqrt{7}*

*=22\sqrt{7}*

Ejemplo 2: *5\sqrt[3]{24}-3\sqrt{81}*

Aquí debemos realizar las descomposiciones de los dos radicandos. Los hacemos dentro de la raíz para más comodidad.

*\sqrt[3]{24}=\sqrt[3]{2^3\cdot 3}=\sqrt[3]{2^3}\sqrt{3}=2\sqrt[3]{3}*

*\sqrt[3]{81}=\sqrt[3]{3^4}=\sqrt[3]{3^3\cdot 3}=\sqrt[3]{3^3}\sqrt[3]{3}=3\sqrt[3]{3}*

Nótese que en la segunda raíz utilizamos la propiedad de producto de potencias de igual base en forma inversa para escribir a *3^4* de forma conveniente y poder cancelar la raíz cúbica.

Ahora, reemplazamos en la expresión original:

*5{\color{green}\sqrt[3]{24}}-3{\color{purple}\sqrt{81}}=5\cdot {\color{green}2\sqrt[3]{3}} -3\cdot {\color{purple}3\sqrt[3]{3}}*

*=10\sqrt[3]{3}-9\sqrt[3]{3}*

*=\sqrt[3]{3}*

Ejemplo 3: *10\sqrt{140}-\sqrt{315}*

Factorizamos y simplificamos:

*\sqrt{140}=\sqrt{2^2\cdot 5\cdot 7}=\sqrt{2^2}\sqrt{5\cdot 7}=2\sqrt{35}*

*\sqrt{315}=\sqrt{3^2\cdot 5\cdot 7}=\sqrt{3^2}\sqrt{5\cdot 7}=3\sqrt{35}*

Reemplazamos y resolvemos:

*10{\color{green}\sqrt{140}}-{\color{purple}\sqrt{315}}=10\cdot {\color{green}2\sqrt{35}}-{\color{purple}3\sqrt{35}}*

*=20\sqrt{35}-3\sqrt{35}*

*=17\sqrt{35}*

Caso 2: Radicales con diferente índice y radicando

Si las raíces no coinciden ni en índice ni radicando, pueden lograrse raíces semejantes mediante la factorización del radicando y la simplificación. Es útil expresar a los radicales como exponentes.

Ejemplo 1: *\sqrt{2}+\sqrt[6]{8}*

A simple vista, no parece que se pueda seguir operando. Sin embargo, en el segundo radical se puede escribir a *8* como *2^3* y luego utilizar la expresión con exponente para llegar a una forma más simple.

*\sqrt[6]{8}=\sqrt[6]{2^3}=2^\frac{3}{6}=2^\frac{1}{2}=\sqrt{2}*

Ahora reemplazamos en la expresión original y resolvemos:

*\sqrt{2}+\sqrt[6]{8}=\sqrt{2}+\sqrt{2}=2\sqrt{2}*

Ejemplo 2: *\sqrt[9]{343}-5\sqrt[6]{49}*

Factorizamos el radicando y expresamos la raíz en forma de exponente para simplificar:

*\sqrt[9]{343}=\sqrt[9]{7^3}=7^\frac{3}{9}=7^\frac{1}{3}=\sqrt[3]{7}*

*\sqrt[6]{49}=\sqrt[6]{7^2}=7^\frac{2}{6}=7^\frac{1}{3}=\sqrt[3]{7}*

Ahora reemplazamos y resolvemos:

*\sqrt[9]{343}-5\sqrt[6]{49}=\sqrt[3]{7}-5\sqrt[3]{7}=-4\sqrt[3]{7}*

Ejemplo 3: *2\sqrt[8]{81}-6\sqrt[4]{144}*

*\sqrt[8]{81}=\sqrt[8]{3^4}=3^\frac{4}{8}=3^\frac{1}{2}=\sqrt{3}*

*\sqrt[4]{144}=\sqrt[4]{2^4\cdot 3^2}=(2^4\cdot 3^2)^\frac{1}{4}=2^\frac{4}{4}\cdot 3^\frac{2}{4}=2\cdot 3^\frac{1}{2}=2\sqrt{3}*

Reemplazamos en la expresión original y resolvemos:

*2\sqrt[8]{81}-6\sqrt[4]{144}=2\sqrt{3}-6\cdot (2\sqrt{3})*

*=2\sqrt{3}-12\sqrt{3}*

*=-10\sqrt{3}*

Caso 3: Radicales con igual radicando y diferente índice

Si dos radicales tienen el mismo radicando pero diferente índice, la suma o resta se deja intacta.

Por ejemplo, *\sqrt{2}+\sqrt[3]{2}* no se puede seguir operando y se deja escrito tal cual.

Ejercicios para practicar

¡Continúa leyendo estos artículos recomendados!

+ Ver infografías