
Operaciones con radicales
En este artículo se explican las operaciones básicas con expresiones radicales: suma, resta, multiplicación, división, potenciación, radicación con ejemplos resueltos. Además, veremos los procesos de simplificación de raíces y la racionalización. Trabajamos con raíces de cualquier índice: cuadradas, cúbicas, etc.
Índice
Suma y resta de radicales
Para sumar o restar radicales estos deben ser semejantes, o sea, las raíces deben ser idénticas. El procedimiento consiste en sumar los coeficientes y copiar la misma raíz.
*a\sqrt[n]{k}+b \sqrt[n]{k}=(a+b) \sqrt[n]{k}*
Si los radicales no son semejantes, se intentan modificar para que lo sean.
Ejemplos:
*5\sqrt{5}+4\sqrt{5}=(5+4)\sqrt{5}=9\sqrt{5}*
*4\sqrt[3]{14}-10\sqrt[3]{14}=(4-10)\sqrt[3]{14}=-6\sqrt[3]{14}*
Puedes ver más ejemplos y qué ocurre con radicales no semejantes en este artículo:
Multiplicación de radicales
Para multiplicar dos radicales, estos deben tener el mismo índice. El procedimiento consiste en multiplicar los coeficientes y los radicandos por separado, estos últimos dentro de una misma raíz con el mismo índice.
*\sqrt[n]{a}\cdot \sqrt[n]{b}=\sqrt[n]{a\cdot b}*
*p\sqrt[n]{a}\cdot q\sqrt[n]{b}=p\cdot q\sqrt[n]{a\cdot b}*
Si los radicales son de diferente índice, es necesario igualarlos hallando un radical equivalente.
Ejemplos:
*-4\sqrt[3]{5}\cdot 6\sqrt[3]{4}=(-4\cdot 6)\sqrt[3]{5\cdot 4}=-24\sqrt[3]{20}*
*3\sqrt{5}\sqrt{2}\sqrt{2}=3\sqrt{5\cdot 2\cdot 2}=3\sqrt{20}*
Mira más ejemplos y qué hacer con radicales de distinto índice en este artículo:
División de radicales
Para dividir dos radicales, estos deben tener igual índice. Lo que se hace es mantener el índice e integrar los radicandos en una misma raíz. Los coeficientes se operan por fuera.
*\dfrac{a\sqrt[n]{p}}{b\sqrt[n]{q}}=\dfrac{a}{b}\sqrt[n]{\dfrac{p}{q}}*
Si los radicales son de diferente índice, es necesario igualarlos primero.
Ejemplos:
*\dfrac{3\sqrt{48}}{4\sqrt{8}}=\dfrac{3}{4}\sqrt{\dfrac{48}{8}}=\dfrac{3}{4}\sqrt{6}*
*\dfrac{6\sqrt{20}}{4\sqrt{5}}=\dfrac{6}{4}\sqrt{\dfrac{20}{5}}=\dfrac{3}{2}\sqrt{4}=\dfrac{3}{2}\cdot 2=3*
Puedes ver más ejemplos y qué hacer con radicales de distinto índice en este artículo:
Operaciones combinadas
Las operaciones combinadas con radicales, también llamadas mixtas, son expresiones que contienen sumas, restas, multiplicaciones y divisiones de raíces. Para resolverlas es importante conocer los procedimientos de cada caso.
Ejemplo:
*5\sqrt{3}\cdot(9\sqrt{2}+7\sqrt{18})=5\sqrt{3}\cdot(9\sqrt{2}+7\sqrt{3^2\cdot 2})=5\sqrt{3}\cdot(9\sqrt{2}+21\sqrt{2})*
*=5\sqrt{3}\cdot(30\sqrt{2})=5\cdot 30\sqrt{3}{\sqrt{2}}=150\sqrt{6}*
Potenciación de radicales
Una raíz elevada a un exponente es igual a elevar el radicando al exponente conservando el mismo índice. Esto es posible por una propiedad de las raíces.
*(\sqrt[n]{a})^m=\sqrt[n]{a^m}*
*(\sqrt{2})^4=\sqrt{2^4}=\sqrt{16}=4*
*(\sqrt[3]{5})^2=\sqrt[3]{5^2}=\sqrt[3]{25}*
*(-\sqrt[5]{4})^6=\sqrt[5]{4^6}=\sqrt[5]{4096}*
Radicación de radicales
La raíz de una raíz es igual a una nueva raíz con igual radicando y con índice igual al producto de los índices originales. Esta igualdad surge por una propiedad de las raíces.
*\sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}*
Ejemplos:
*\sqrt[4]{\sqrt[6]{7}}=\sqrt[4\cdot 6]{7}=\sqrt[24]{7}*
*\sqrt{\sqrt[3]{5}}=\sqrt[2\cdot 3]{5}=\sqrt[6]{5}*
*\sqrt{\sqrt[5]{\sqrt{14}}}=\sqrt[2\cdot 5\cdot 2]{14}=\sqrt[20]{14}*
Simplificación
Simplificar un radical consiste en escribirlo de la forma más sencilla posible, de modo que tenga el menor índice, no pueda extraerse ningún factor del radicando y no haya fracciones en este.
Ejemplos:
*\sqrt[3]{7^3}=7*
*\sqrt[7]{20^{14}}=20^{\frac{14}{7}}=20^2=400*
*\sqrt[3]{2^{11}}=2^3\sqrt[3]{2^2}=8\sqrt[3]{4}*
Mira más ejemplos y procedimientos en el siguiente artículo:
Racionalización
Racionalizar es reescribir un cociente de modo que se remuevan los radicales del numerador o del denominador.
Ejemplos:
*\dfrac{1}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{2}}{(\sqrt{2})^2}=\dfrac{\sqrt{2}}{2}*
*\dfrac{\sqrt{8}}{\sqrt{3}}=\dfrac{\sqrt{8}}{\sqrt{3}}\cdot \dfrac{\sqrt{8}}{\sqrt{8}}=\dfrac{(\sqrt{8})^2}{\sqrt{3\cdot 8}}=\dfrac{8}{\sqrt{24}}*
*\dfrac{1}{\sqrt[3]{7}}=\dfrac{1}{\sqrt[3]{7}}\cdot \dfrac{\sqrt[3]{7^2}}{\sqrt[3]{7^2}}=\dfrac{\sqrt[3]{7^2}}{\sqrt[3]{7^3}}=\dfrac{\sqrt[3]{49}}{7}*
Mira más ejemplos y casos de racionalización en el siguiente artículo:
Bibliografía
- Abálsamo, R., Berio, A., Kotowski, C., Liberto, L., Mastucci, S. y Quirós, N. (2013). Matemática 3. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 4. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.

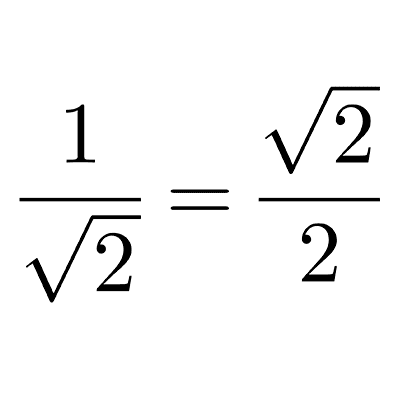





Deja una respuesta