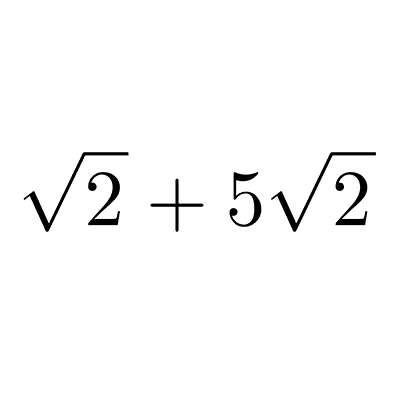
Radicales en matemáticas
En este artículo explicamos qué son los radicales en el contexto matemático, algunos ejemplos, propiedades y las operaciones que pueden realizarse entre ellos.
Índice
¿Qué son los radicales?
En matemáticas, los radicales son una notación utilizada para representar las raíces de un número o de una expresión algebraica.
El símbolo más común para representar un radical es el radical principal *\sqrt{~}*, que se utiliza para la raíz cuadrada. Por ejemplo, *\sqrt{9}* representa la raíz cuadrada principal de 9, que es igual a 3, ya que *3^2=9.*
Las partes de un radical son:
- Índice: Es el número que indica qué tipo de raíz se está tomando. Por ejemplo, en la raíz cuadrada, el índice es 2, en la raíz cúbica, el índice es 3, y así sucesivamente.
- Símbolo radical: Es el símbolo *\sqrt{~}* que representa la operación de encontrar la raíz.
- Radicando: Es el número bajo el signo radical, del cual se busca la raíz.
Los números radicales pueden ser simples, como la raíz cuadrada o la raíz cúbica de un número específico, pero también pueden ser más complejos, involucrando otras expresiones algebraicas. Por ejemplo, *\sqrt{x^2 + 2x + 1}* representa la raíz cuadrada de la expresión *x^2+2x+1.*
Generalmente, los tipos de radicales se determinan a partir a sus índices, de este modo tenemos:
- Radicales cuadráticos o raíces cuadradas donde el índice es 2; por ejemplo *\sqrt{5},* *~~\sqrt{9},* *\sqrt{x+6}.*
- Radicales cúbicos o raíces cúbicas, donde el índice es 3; por ejemplo *\sqrt[3]{6},* *~~\sqrt[3]{y+4},* *~~\sqrt[3]{x^2+3}.*
- Radicales enésimos o raíces enésimas, donde el índice es cualquier número entero positivo n; por ejemplo: *\sqrt[5]{8},* *~~\sqrt[8]{9x},* *~~\sqrt[10]{x^3-1}.*
Los radicales se pueden usar para representar una variedad de cantidades, como longitudes, áreas y volúmenes. Por ejemplo, la raíz cuadrada de un área es el lado de un cuadrado con esa área. La raíz cúbica de un volumen es el lado de un cubo con ese volumen.
Ejemplos de radicales
A continuación, se presentan diez ejemplos de expresiones radicales: *\sqrt{7};* *~~\sqrt[3]{-13};* *~~\sqrt{x^2 + 2x + 1};* *~~\sqrt[3]{5};* *~~\sqrt[4]{\dfrac{x^3 +3x^2}{x-1}};* *~~\sqrt[7]{6};* *~~\sqrt{9x};* *~~\sqrt[4]{-3x+1};* *~~\sqrt[3]{\dfrac{-6z}{x}};* *~~\sqrt{16x^2-9y^2}.*
Es importante señalar que las raíces de índice par de números negativos no existen en el campo de los números reales, por ejemplo: *\sqrt{-1}* no es un número real. En cambio, las raíces de índice impar de números negativos sí existen, por ejemplo, *\sqrt[3]{-8}.*
Operaciones con radicales
Las operaciones básicas con números radicales se pueden realizar siempre que se cumplan algunas condiciones. Es útil conocer las propiedades de los radicales ya que permiten resolver problemas de manera más sencilla.
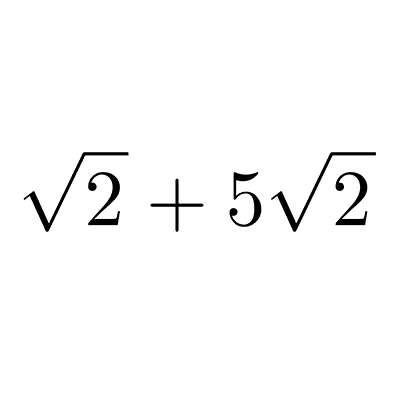

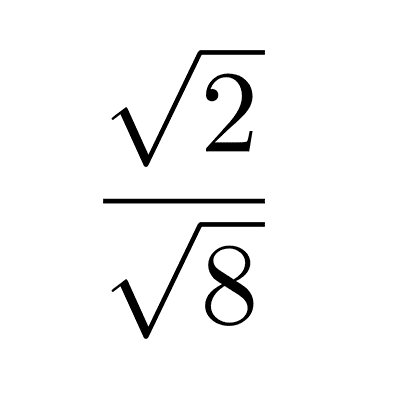
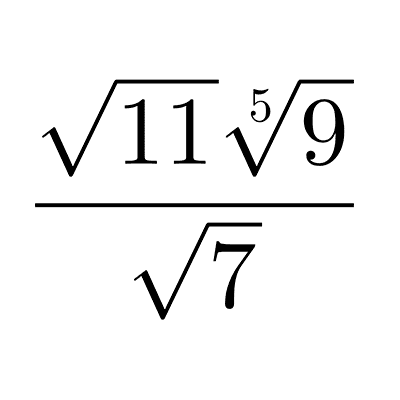
Simplificación y racionalización
La racionalización es un proceso que consiste en remover expresiones radicales ya sea de un denominador o un denominador. La simplificación consiste en encontrar la forma más simple de escribir a un mismo radical.
Bibliografía
- Abálsamo, R., Berio, A., Kotowski, C., Liberto, L., Mastucci, S. y Quirós, N. (2013). Matemática 3. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 4. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.

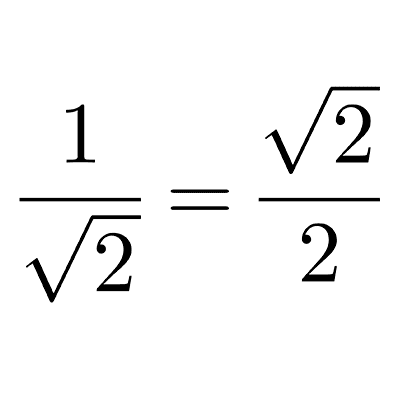
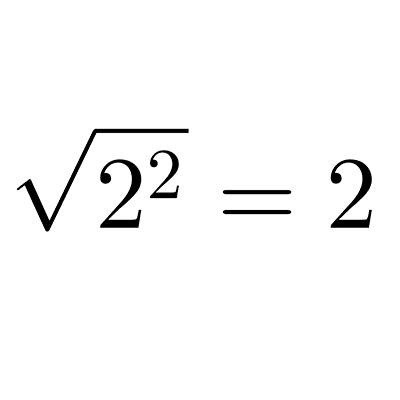
Deja una respuesta