División de radicales
En este artículo explicamos cómo resolver divisiones de raíces, tanto si tienen índices iguales como si los tienen diferentes, con ejercicios resueltos paso por paso.
Índice
División de radicales de igual índice
Cuando dos radicales tienen el mismo índice se llaman homogéneos. El número que multiplica a la raíz se llama coeficiente. Por ejemplo: *\sqrt{8}* y *4\sqrt{11}* son radicales homogéneos, sus coeficientes son 1 y 4 respectivamente.
Para dividir radicales con igual índice, se mantiene el índice y se integran en una misma raíz los radicandos. Los coeficientes se dividen por fuera.
*\dfrac{a\sqrt[n]{p}}{b\sqrt[n]{q}}=\dfrac{a}{b}\sqrt[n]{\dfrac{p}{q}}*
El cociente entre raíces también se puede expresar como *\sqrt[n]{p}:\sqrt[n]{q},* pero en nuestros ejemplos usaremos raya fraccionaria para más comodidad.
Ejemplo 1
*\dfrac{\sqrt{2}}{\sqrt{8}}*
Los coeficientes de ambos radicales son 1, para hallar el cociente integramos los dos radicandos dentro de una misma raíz.
*\dfrac{\sqrt{2}}{\sqrt{8}}=\sqrt{\dfrac{2}{8}}*
*=\sqrt{\dfrac{1}{4}}*
*=\dfrac{1}{2}*
Es conveniente, si se puede, simplificar la raíz resultante de la operación.
Ejemplo 2
*\dfrac{3\sqrt{40}}{4\sqrt{8}}*
Seguimos el mismo procedimiento que antes pero dividiendo los radicales dentro de una misma raíz y los coeficientes por fuera.
*\dfrac{3\sqrt{40}}{4\sqrt{8}}=\dfrac{3}{4}\sqrt{\dfrac{40}{8}}*
*=\dfrac{3}{4}\sqrt{5}*
Ejemplo 3
*\dfrac{-\sqrt[3]{4}}{3\sqrt[3]{-9}}*
Las reglas de los signos se aplican tanto para los coeficientes como para los radicandos y se procede de igual forma que antes.
*\dfrac{-\sqrt[3]{4}}{3\sqrt[3]{-9}}=-\dfrac{1}{3}\sqrt[3]{\dfrac{4}{-9}}*
*-\dfrac{1}{3}\sqrt[3]{-\dfrac{4}{9}}*
Ejemplo 4
Si en las divisiones aparecen variables (letras) en los coeficientes o radicandos, se siguen las mismas reglas que vimos hasta ahora. Aquí vemos dos casos:
*\dfrac{a\sqrt{6}}{b\sqrt{n}}=\dfrac{a}{b}\sqrt{\dfrac{6}{n}}*
*\dfrac{4\sqrt[5]{w}}{2\sqrt[5]{k}}=\dfrac{4}{2}\sqrt[5]{\dfrac{w}{k}}=2\sqrt[5]{\dfrac{w}{k}}*
Ejemplo 5
*\dfrac{\sqrt[3]{56}+\sqrt[3]{189}}{-5\sqrt[3]{7}}*
En este ejemplo, el numerador es una suma de raíces, para resolver la operación podemos primero distribuir el denominador entre los sumandos y luego proceder como es habitual en cada caso.
*\dfrac{\sqrt[3]{56}+\sqrt[3]{189}}{-5\sqrt[3]{7}}=\dfrac{\sqrt[3]{56}}{-5\sqrt[3]{7}}+\dfrac{\sqrt[3]{189}}{-5\sqrt[3]{7}}*
*=-\dfrac{1}{5}\sqrt[3]{\dfrac{56}{7}}-\dfrac{1}{5}\sqrt[3]{\dfrac{189}{7}}*
*=-\dfrac{1}{5}\sqrt[3]{8}-\dfrac{1}{5}\sqrt[3]{27}*
*=-\dfrac{1}{5}\cdot 2-\dfrac{1}{5}\cdot 3*
*=-1*
Ejercicios para practicar: resolver las siguientes divisiones.
- *\dfrac{5\sqrt[5]{-243}}{\sqrt[5]{-81}}*
- *\dfrac{-7\sqrt{27}}{2\sqrt{12}}*
- *\dfrac{-4\sqrt{27}+5\sqrt{12}}{\sqrt{3}}*
- *\dfrac{6\sqrt{20}}{4\sqrt{5}}*
Soluciones:
- *\dfrac{5\sqrt[5]{-243}}{\sqrt[5]{-81}}=5\sqrt[5]{\dfrac{-243}{-81}}=5\sqrt[5]{3}*
- *\dfrac{-7\sqrt{27}}{2\sqrt{12}}=-\dfrac{7}{2}\sqrt{\dfrac{27}{12}}=-\dfrac{7}{2}\sqrt{\dfrac{9}{4}}=-\dfrac{7}{2}\cdot \dfrac{3}{2}=-\dfrac{21}{4}*
- *\dfrac{-4\sqrt{27}+5\sqrt{12}}{\sqrt{3}}=\dfrac{-4\sqrt{27}}{\sqrt{3}}+\dfrac{5\sqrt{12}}{\sqrt{3}}=-4\sqrt{\dfrac{27}{3}}+5\sqrt{\dfrac{12}{3}}=-4\sqrt{9}+5\sqrt{4}=-4\cdot 3+5\cdot 2=-2*
- *\dfrac{6\sqrt{20}}{4\sqrt{5}}=\dfrac{6}{4}\sqrt{\dfrac{20}{5}}=\dfrac{3}{2}\sqrt{4}=\dfrac{3}{2}\cdot 2=3*
División de radicales de distinto índice
Dos radicales de distinto índice se llaman heterogéneos. Por ejemplo: *\sqrt[6]{3}* y *\sqrt[3]{5}* son radicales heterogéneos.
Para dividir radicales con distinto índice, primero es necesario igualarlos. Luego, efectuar el proceso como se vio anteriormente.
Para igualar los índices hay que realizar lo siguiente:
- Hallar el mínimo común múltiplo de los índices.
- Dividir el MCM entre cada uno de los índices.
- Multiplicar el valor obtenido en el paso anterior por los índices originales y el exponente del radicando correspondiente.
Tratamos más a detalle la igualación de índices en el artículo sobre multiplicación de radicales. Léelo para más información.
Con la siguiente calculadora podrás obtener rápidamente el Mínimo Común Múltiplo entre dos o más números:
Ejemplo 1
*\dfrac{\sqrt{14}}{\sqrt[8]{5}}*
1. Hallamos el MCM de los índices.
*MCM(2,8)=8*
2. Dividimos el MCM entre cada índice.
Primera raíz: *\dfrac{8}{2}=4*
Segunda raíz: *\dfrac{8}{8}=1*
3. Multiplicamos los valores obtenidos por los índices y exponentes de la raíz que corresponda.
Primera raíz: *\sqrt{14}=\sqrt[2\cdot 4]{14^4}=\sqrt[8]{38416}*
Segunda raíz: *\sqrt[8]{5}=\sqrt[8\cdot 1]{5^1}=\sqrt[8]{5}*
Ahora que son iguales los índices, podemos operar como sabemos.
*\dfrac{\sqrt{14}}{\sqrt[8]{5}}=\dfrac{\sqrt[8]{38416}}{\sqrt[8]{5}}=\sqrt[8]{\dfrac{38416}{5}}*
Ejemplo 2
*\dfrac{4\sqrt[6]{2}}{5\sqrt[9]{2}}*
1. Hallamos el MCM de los índices.
*MCM(6,9)=18*
2. Dividimos el MCM entre cada índice.
Primera raíz: *\dfrac{18}{6}=3*
Segunda raíz: *\dfrac{18}{9}=2*
3. Multiplicamos los valores obtenidos por los índices y exponentes de la raíz que corresponda.
Primera raíz: *\sqrt[6]{2}=\sqrt[6\cdot 3]{2^3}=\sqrt[18]{8}*
Segunda raíz: *\sqrt[8]{2}=\sqrt[9\cdot 2]{2^2}=\sqrt[18]{4}*
Ahora procedemos a dividir:
*\dfrac{4\sqrt[6]{2}}{5\sqrt[9]{2}}=\dfrac{4\sqrt[18]{8}}{5\sqrt[18]{4}}*
*=\dfrac{4}{5}\sqrt[18]{\dfrac{8}{4}}*
*=\dfrac{4}{5}\sqrt[18]{2}*
Ejercicios de práctica: resolver las siguientes divisiones.
- *\dfrac{5\sqrt[3]{12}}{\sqrt{2}}*
- *\dfrac{4\sqrt{3}}{\sqrt[4]{2}}*
- *\dfrac{3\sqrt{10}-2\sqrt[3]{5}}{\sqrt{2}}*
- *\dfrac{2\sqrt[4]{5}}{\sqrt[3]{4}}*
Soluciones:
- *\dfrac{5\sqrt[3]{12}}{\sqrt{2}}=\dfrac{5\sqrt[6]{12^2}}{\sqrt[6]{2^3}}=5\sqrt[6]{\dfrac{12^2}{2^3}}=5\sqrt[6]{18}*
- *\dfrac{4\sqrt{3}}{\sqrt[4]{2}}=\dfrac{4\sqrt[4]{3^2}}{\sqrt[4]{2}}=4\sqrt[4]{\dfrac{3^2}{2}}=4\sqrt[4]{\dfrac{9}{2}}*
- *\dfrac{3\sqrt{10}-2\sqrt[3]{5}}{\sqrt{2}}=\dfrac{3\sqrt{10}}{\sqrt{2}}-\dfrac{2\sqrt[3]{5}}{\sqrt{2}}=3\sqrt{\dfrac{10}{2}}-\dfrac{2\sqrt[6]{5^2}}{\sqrt[6]{2^3}}=3\sqrt{5}-2\sqrt[6]{\dfrac{25}{8}}*
- *\dfrac{2\sqrt[4]{5}}{\sqrt[3]{4}}=\dfrac{2\sqrt[12]{5^3}}{\sqrt[12]{4^4}}=2\sqrt[12]{\dfrac{125}{256}}*
Bibliografía
- Abálsamo, R., Berio, A., Kotowski, C., Liberto, L., Mastucci, S. y Quirós, N. (2013). Matemática 3. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 4. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.

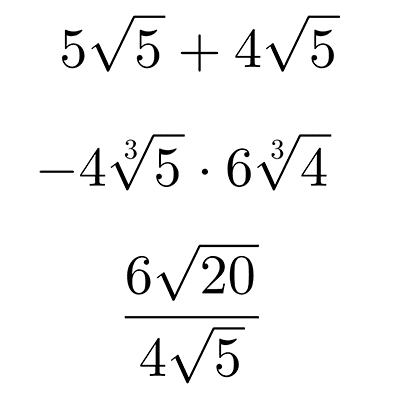



Deja una respuesta