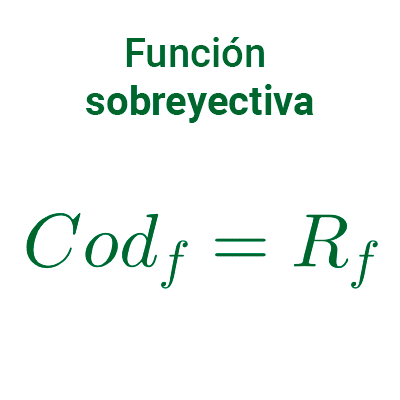
Función biyectiva
En este artículo explicamos qué es una función biyectiva con ejemplos y cómo reconocer si una función es biyectiva o no.
Índice
¿Qué es una función biyectiva?
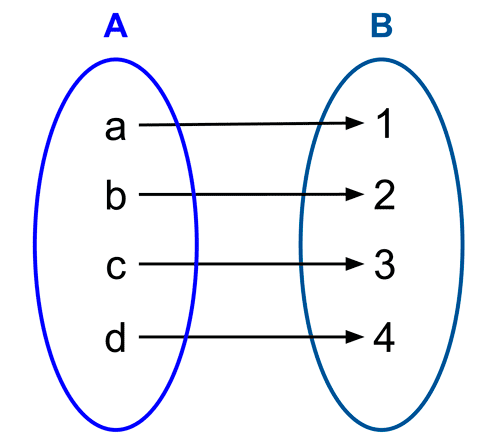
Una función biyectiva es aquella que es inyectiva y sobreyectiva a la vez, es decir: no existen dos valores del dominio que tengan la misma imagen y todo valor del codominio es imagen de algún elemento del dominio.
En las funciones biyectivas queda establecida una correspondencia biunívoca entre los elementos del dominio y el codominio: cada elemento del dominio corresponde a un único valor del codominio y viceversa.
Formalmente, una función f con dominio A y codominio B es biyectiva si ocurre que:
*∀y∈B~ ∃!x∈A~/~y=f(x)*
Es decir: para todo valor y del codominio existe un único valor x del dominio tal que y es la imagen de x a través de f.
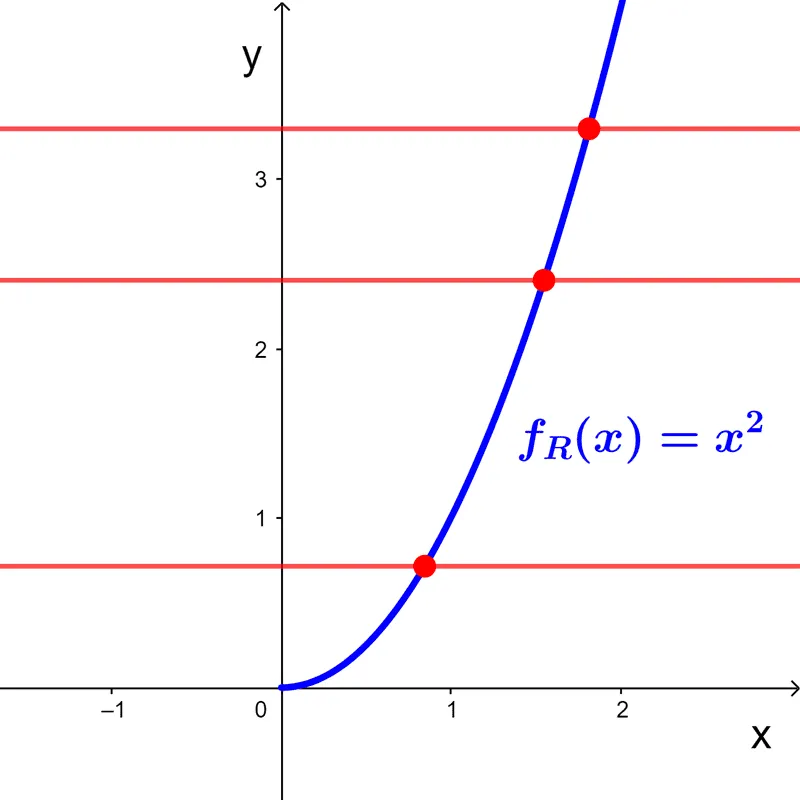
Una función que no es inyectiva o que no es sobreyectiva (o ambas) se dice que es no biyectiva. Así pues, la función cuadrática *y=x^2* no es biyectiva porque:
- Existen elementos del dominio que tienen la misma imagen, por ejemplo, *x=2* y *x=-2* tienen como imagen a *y=4,* resultando en que la función no es inyectiva.
- El codominio es *\mathbb{R}* y es diferente del rango *[0,+\infty),* por tanto, la función no es sobreyectiva.
Por otro lado, la función cúbica *y=x^3* sí es biyectiva porque no hay dos valores del dominio que tengan la misma imagen y el codominio es igual al rango. La función raíz cuadrada *y=\sqrt{x}* es inyectiva pero no es sobreyectiva, por lo tanto, no es biyectiva. Más adelante veremos cómo se puede arreglar una función para que cumpla la biyectividad.
La importancia de las funciones biyectivas reside en que son las únicas para las cuales existe una función inversa y esta también es biyectiva. Esto es porque, al haber una correspondencia de uno a uno, podríamos invertir la relación y a cada elemento del codominio correspondería uno del dominio, formándose una nueva función.
Algunos ejemplos de funciones biyectivas en la vida cotidiana pueden ser:
- Entre vehículos y matrículas: cada vehículo tiene una matrícula única que lo identifica y cada matrícula identifica un único vehículo.
- Entre productos y códigos de barra: cada producto en un supermercado tiene un único código de barras y cada código de barras corresponde a un único producto.
- Entre personas e identificaciones: toda persona tiene una única identificación (DNI, pasaporte, cédula, etc.) y cada identificación corresponde a una única persona.
¿Cómo saber si una función es biyectiva?
Para determinar si una función es biyectiva se debe comprobar que sea inyectiva y sobreyectiva, es decir: que no existan imágenes repetidas y que el codominio sea igual al rango.
Para probar la inyectividad podemos usar la prueba de la recta horizontal: verificar que cualquier recta horizontal corta la gráfica de la función a lo sumo en un punto. También es posible usar una comprobación algebraica. Para determinar la sobreyectividad debemos recurrir al análisis del codominio y el rango con el fin de verificar que sean iguales.
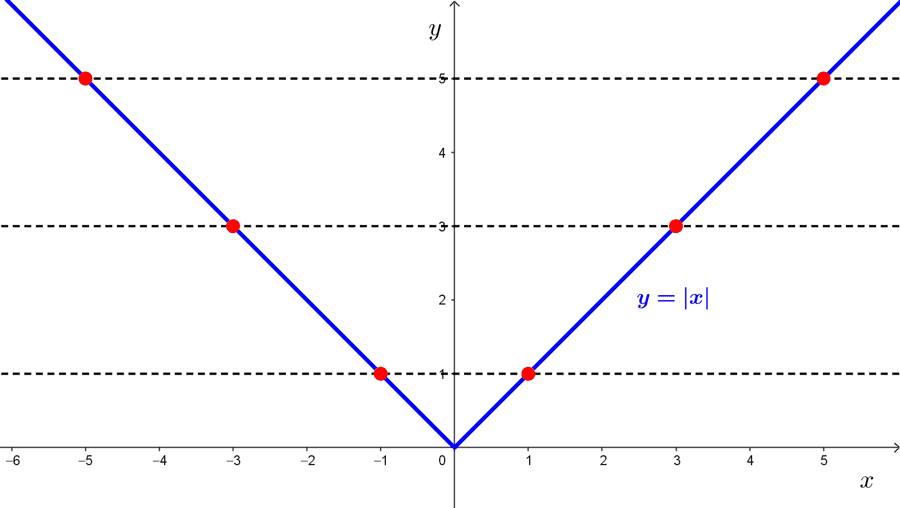
Ejemplo 1: determinar si la función valor absoluto *y=|x|* es biyectiva.
1) Análisis de inyectividad: con el gráfico de la función en el plano cartesiano, la sometemos a la prueba de la recta horizontal y vemos que hay rectas que cortan la curva en más de un punto. Por lo tanto, la función no es inyectiva.
Algebraicamente se puede encontrar algún caso en el que dos valores diferentes tienen la misma imagen. Por ejemplo, *x=-1* y *x=1* son diferentes y tienen como valor absoluto a *y=1.*
2) Análisis de sobreyectividad: el codominio de toda función real, si no se especifica algo diferente, es *\mathbb{R}.* El rango de la función valor absoluto es el intervalo *[0,+\infty).* Como *\mathbb{R}\neq [0,+\infty),* la función no es sobreyectiva.
Conclusión: como la función valor absoluto no es inyectiva ni sobreyectiva, no es biyectiva.
Ejemplo 2: analizar si la función cúbica *g(x)=x^3* es biyectiva.
1) Inyectividad: la función pasa la prueba de la recta horizontal, esto quiere decir que no hay dos valores del dominio que tengan la misma imagen. Entonces, la función es inyectiva.
2) Sobreyectividad: el codominio de esta función es *\mathbb{R}* y, como el rango de toda función cúbica es *\mathbb{R},* se tiene que el codominio y el rango son iguales. Por tanto, la función es sobreyectiva.
Conclusión: como esta función cúbica es inyectiva y sobreyectiva, entonces es biyectiva.
Ejemplo 3: probar si la función lineal *h(x)=2x+1* es biyectiva.
1) Inyectividad: con la gráfica en el plano usamos la prueba de la recta horizontal y determinamos que la función es inyectiva.
2) Sobreyectividad: el codominio de esta función es *\mathbb{R}.* Como el rango de toda función lineal no constante es *\mathbb{R},* se tiene que el codominio y el rango son iguales, por tanto, la función es sobreyectiva.
Conclusión: como la función es inyectiva y sobreyectiva, es biyectiva.
Restricciones de dominio y codominio
Cuando una función no es biyectiva, es posible lograr que lo sea restringiendo su dominio y codominio de modo que los conjuntos resultantes permitan la inyectividad y sobreyectividad.
Por ejemplo, al principio vimos que la función cuadrática *f(x)=x^2* no era biyectiva porque no era ni inyectiva ni sobreyectiva. Si realizamos una restricción del dominio a solo valores no negativos, es decir, el intervalo *[0,+\infty),* la función pasa la prueba de la recta horizontal porque ya no existen imágenes repetidas.
Ahora, si restringimos el codominio a solo los valores reales no negativos, este conjunto será igual al rango, resultando en que la función es también sobreyectiva. Como la función restringida es inyectiva y sobreyectiva, entonces es biyectiva.
Ejemplos
Las siguientes afirmaciones pueden ser de utilidad a la hora de determinar si una función es biyectiva o no.
- Todas las funciones lineales no constantes son biyectivas.
- Las funciones constantes no son biyectivas.
- Las funciones potenciales de la forma *y=x^n,* donde n es un entero positivo, son biyectivas cuando n es impar y no son biyectivas cuando n es par.
- Las funciones logarítmicas son biyectivas, las exponenciales también si se restringe su codominio.
- Las funciones radicales de la forma *y=\sqrt[n]{x},* donde n es un entero positivo, son biyectivas sin n es impar y no son biyectivas si n es par (se puede solucionar restringiendo el codominio).
- Las funciones trigonométricas seno, coseno y tangente no son biyectivas, pero es posible realizar restricciones de dominio y codominio para que lo sean.
Ejemplos de funciones biyectivas:
- *y=2x+5*
- *y=-x+1*
- *y=x^5+3*
- *y=\sqrt[3]{x}*
- *y=\ln(x)*
Ejemplos de funciones no biyectivas:
- *y=-3*
- *y=x^2+2*
- *y=x^3+2x^2*
- *y=\dfrac{x^2}{x-1}*
Preguntas frecuentes
¿Cuáles son las propiedades de las funciones biyectivas?
Las propiedades de las funciones biyectivas son las siguientes:
1. No hay elementos diferentes del dominio que tengan la misma imagen.
2. Todos los elementos del codominio tienen un preimagen en el dominio.
3. Existe una función inversa que también es biyectiva.
¿Cómo se puede demostrar que una función es biyectiva?
Para demotrar que una función es biyectiva se debe comprobar que es inyectiva y sobreyectiva, es decir: que no existen imágenes repetidas y que el codominio es igual al rango.
¿Cómo se puede demostrar que una función no es biyectiva?
Para demostrar que una función no es biyectiva se puede encontrar al menos dos elementos que tengan la misma imagen (funcion no inyectiva), o encontrar algún elemento del codominio que no tenga preimagen (función no sobreyectiva).
