Valor absoluto de un número real
0 - Votos: 0
En este artículo explicamos el concepto de valor absoluto de un número real, sus propiedades y cómo calcularlo de forma sencilla.
Índice
¿Qué es el valor absoluto?
El valor absoluto de un número real es un número no negativo que representa su distancia al cero en la recta numérica. En otras palabras, es la cantidad que hay que sumar o restar al número para llegar a cero. Se representa simbólicamente con dos barras verticales | | alrededor del número.
Matemáticamente, el valor absoluto de un número real, también llamado módulo o valor modular, se define de la siguiente manera:
- Si el número es positivo o cero, su valor absoluto es el mismo número. Simbólicamente: *|a|=a* si *a≥0.*
- Si el número es negativo, entonces su valor absoluto es su opuesto, es decir, el número cambiado de signo. Simbólicamente: *|a|=-a* si *a<0.*
¿Cómo calcular el valor absoluto?
Para calcular el valor absoluto de un número real, debemos considerar solamente la magnitud del número: si el número es positivo o cero, se lo expresa tal cual; si el número es negativo, se lo cambia de signo. El valor absoluto siempre es una cantidad no negativa, independientemente del signo del número original.
Ejemplos
*|12|=12* porque 12 es un número positivo. La distancia entre 0 y 12 en la recta numérica es doce unidades.
*|-2|=2* porque -2 es un número negativo. La distancia entre -2 y 0 en la recta numérica es de dos unidades.
*|0|=0* porque la distancia del 0 al 0 es de cero unidades. El valor absoluto de cero es cero.
Del mismo modo, se puede calcular el valor absoluto para otros números enteros, racionales, decimales, irracionales, etc.
*|7/4|=7/4~* porque *~7/4≥0*
*|-3/5|=3/5~* porque *~-3/5<0*
*|-9|=9*
*|6|=6*
*|\sqrt[3]{7}|=\sqrt[3]{7}*
*|-6,5|=6,5*
*|-2,3|=2,3*
*|\sqrt{2}-2|=2-\sqrt{2}~* porque *~\sqrt{2}-2~* es una expresión negativa.
Podemos tener operaciones dentro del valor absoluto. Sus barras funcionan como paréntesis, debemos operar primero dentro antes de calcularlo.
*|2+5|=|7|=7*
*|-5-5|=|-10|=10*
*|2,5-4|=|-1,5|=1,5*
*|\sqrt{2}-\sqrt{2}|=|0|=0*
*|(-2)(-3)|=|6|=6*
*\left|-\dfrac{5}{3}+\dfrac{2}{4}\right|=\left|-\dfrac{7}{6}\right|=\dfrac{7}{6}*
Valor absoluto en la recta numérica
Para cualquier número real y su opuesto, la distancia al origen es la misma. Por ejemplo, -10 y 10 están ambos a diez unidades de distancia del cero, o sea, *|10|=|-10|=10.* En general, si *a* es un número real y *-a* es su opuesto, entonces *|a|=|-a|.* Esta es una de las propiedades del valor absoluto.
Distancia entre dos números
Si deseamos conocer la distancia entre, por ejemplo, *6* y *15* en la recta real, podemos restar al mayor número el menor y obtenerla: *15-6=9.* Entonces, hay *9* unidades de distancia entre esos números. Teniendo a nuestra disposición el concepto de valor absoluto, ya no es necesario preocuparnos por ubicar bien los números al realizar la diferencia, pues el resultado siempre será positivo.
Para calcular la distancia entre dos números reales, realizamos el valor absoluto de su diferencia. Si *a* y *b* son números reales, la distancia entre ellos es:
*d(a,b)=|a-b|*
Ejemplos
- La distancia entre 10 y 7 es *|10-7|=|3|=3*
- La distancia entre 5 y -3 es *|5-(-3)|=|5+3|=|8|=8*
- La distancia entre -3 y -5 es *|-3-(-5)|=|-3+5|=|2|=2*
Nótese que *|a-b|=|b-a|,* por lo tanto no importa el orden de la sustracción. Podríamos haber llegado al mismo resultado cambiando el lugar de los números. La distancia entre *0* y un número *a* es: *|a-0|=|a|,* que concuerda con la interpretación geométrica del valor absoluto que vimos al principio.
El concepto de valor absoluto se aplica siempre que nos interese la magnitud o valor numérico de un número real sin que importe su signo. Por ejemplo:
- En geometría, se utiliza para calcular distancias entre puntos en un plano, como vimos recién.
- En física, puede representar magnitudes físicas como velocidad, aceleración o fuerza, donde la dirección no es relevante.
- En programación y análisis de algoritmos, puede ser útil para calcular diferencias o distancias entre valores.
- En estadística, se utiliza en la medida de dispersión, como en el cálculo de la desviación absoluta o en la distancia entre valores en un conjunto de datos.
Valor absoluto como una raíz cuadrada
Recuerde que la expresión *\sqrt{~}* significa “raíz cuadrada positiva de…”. Por tanto, la ecuación *\sqrt{a^2}=a* no siempre es verdadera; lo es solo cuando *a≥0,* de otro modo no puede cancelarse la raíz. Si *a<0,* entonces *-a>0,* de modo que tenemos *\sqrt{a^2}=-a.*
Resumimos este razonamiento de la siguiente forma:
- *\sqrt{a^2}=a* si *a≥0*
- *\sqrt{a^2}=-a* si *a<0*
Es notable la enorme similitud con la definición del valor absoluto, por esto se adopta como una definición alternativa del mismo.
El valor absoluto de un número real es igual a la raíz cuadrada de su cuadrado:
*|a|=\sqrt{a^2}*
Ejemplos
*|-2|=\sqrt{(-2)^2}=\sqrt{4}=2*
*|5|=\sqrt{5^2}=\sqrt{25}=5*
*|-3,5|=\sqrt{(-3,5)^2}=\sqrt{12,25}=3,5*
Propiedades del valor absoluto
Veremos a continuación algunas propiedades fundamentales del valor absoluto.
- El valor absoluto de una cantidad siempre es no negativo: *|a|≥0*
- El valor absoluto de un número es cero sólo cuando el número es cero: *|a|=0* si y sólo si *a=0*
- El valor absoluto de un número es igual al de su opuesto: *|a|=|-a|*
- El valor absoluto siempre es mayor o igual que el número original: *|a|≥a.* Será mayor cuando el número original sea negativo. Será igual cuando el número sea no negativo.
- Si el valor absoluto de un número *a* es menor que *b,* entonces a está entre b y su opuesto. Si *|a|<b,* entonces *-b<a<b.*
- Si el valor absoluto de un número *a* es mayor que *b,* entonces *a* es mayor que *b* o *a* es menor que *-b.* Si *|a|>b,* entonces *a>b* o *a<-b*
- El valor absoluto del producto es igual al producto de los valores absolutos de los factores: *|ab|=|a||b|*
- El valor absoluto de un cociente es igual al cociente de los valores absolutos de numerador entre denominador: *\left|\dfrac{a}{b}\right|=\dfrac{|a|}{|b|}* con *b≠0*
- El valor absoluto de una suma es menor o igual a la suma de los valores absolutos de los términos. *|a+b|≤|a|+|b|.* Esto se denomina desigualdad triangular.
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 4. Puerto de Palos.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.


Subir


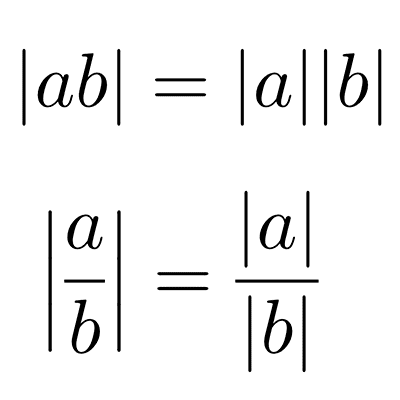

Deja una respuesta