Teorema del sándwich

0 - Votos: 0

En este artículo estudiamos un teorema importante y muy conocido sobre límites que permite el cálculo más sencillo de otros: el teorema de compresión o del sándwich. Además, veremos algunos ejemplos de aplicación del mismo.

Índice

Enunciado del teorema

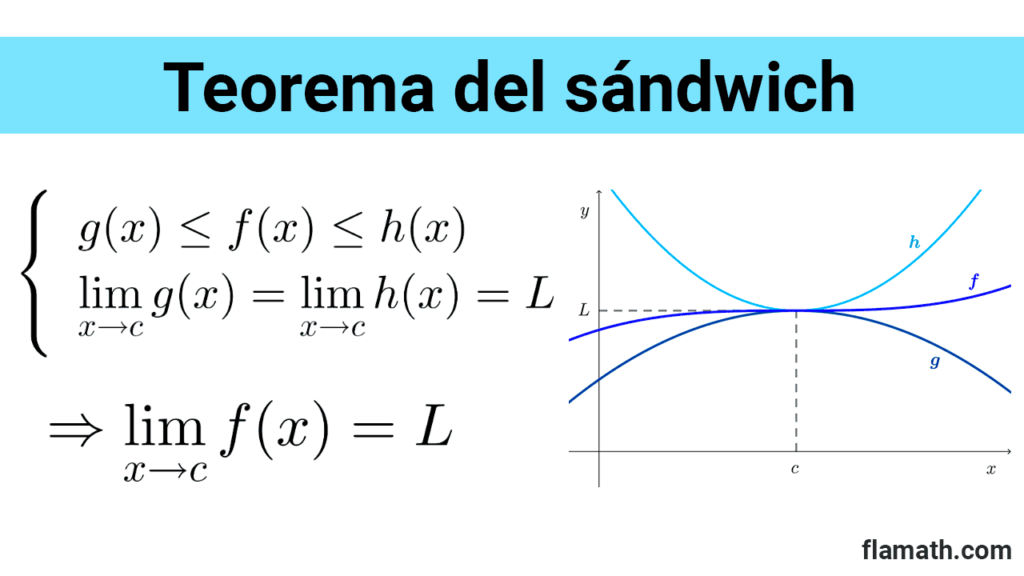
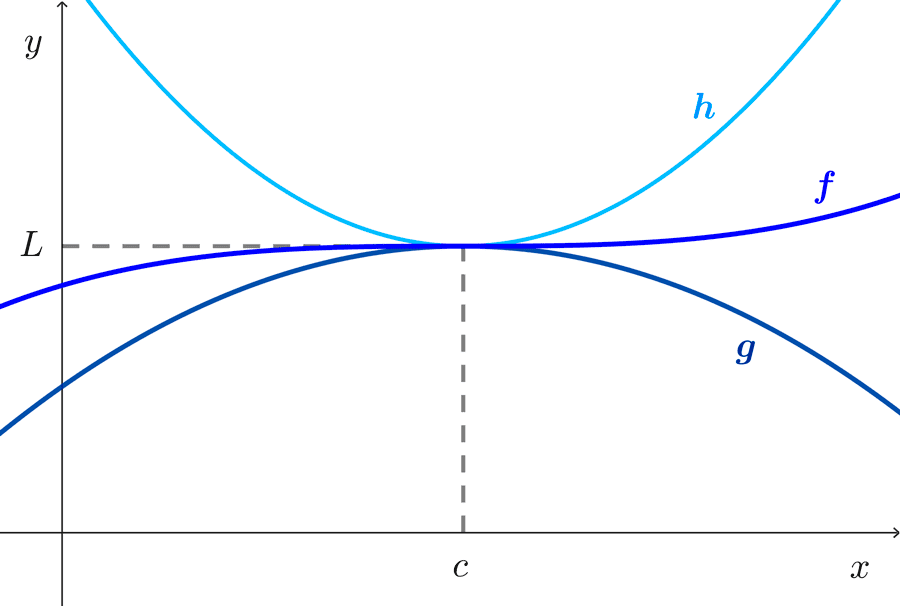
El teorema del sándwich nos dice que si una función está atrapada entre otras dos funciones cerca de un punto y estas dos funciones tienen el mismo límite en el punto, entonces la primera función está forzada a tener el mismo límite en el punto.

Teorema del sándwich: si *g(x)≤f(x)≤h(x)* cuando x es cercana a c (excepto posiblemente en c) y existen los límites de g y h en c, y son iguales a L, *\lim_{x\to c} g(x)=\lim_{x\to c} h(x)=L,* entonces también existe el límite de f en c y es igual a L:

$$\lim_{x\to c} f(x)=L$$

Gráfico explicativo del teorema del sándwich de límites — Teorema del sándwich

Este teorema es de gran utilidad a la hora de hallar límites, entre ellos el límite trigonométrico fundamental.

Nota: el teorema del sándwich también recibe los siguientes nombres según la bibliografía que se consulte.

Teorema de compresión.
Teorema de interposición.
Teorema del emparedado.
Teorema de contracción.
Teorema de interpolación.
Teorema del encaje.

Ejemplos de aplicación del teorema del sándwich

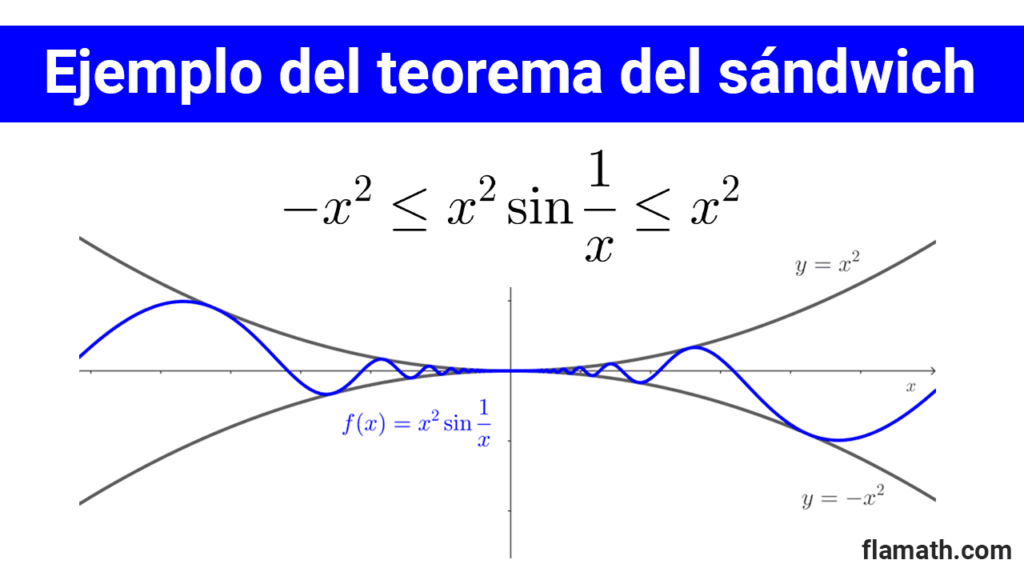
Ejemplo 1: Hallar *\lim_{x\to 0} x^2 \sin \dfrac{1}{x}*

Solución: Primero observamos que no podemos usar la propiedad del producto, pues esto daría

*\lim_{x\to 0} x^2 \sin(1/x)=\lim_{x\to 0} x^2\cdot \lim_{x\to 0} \sin(1/x),* pero *\lim_{x\to 0} \sin(1/x)* no existe.

En lugar de esto podemos aplicar el teorema del sándwich y por tanto necesitamos hallar una función g menor a *f(x)=x^2 \sin(1/x)* y una función h mayor a f tal que g y h tengan el mismo límite en cero. Como sabemos que la función seno se encuentra entre -1 y 1, podemos escribir:

*-1≤\sin \dfrac{1}{x}≤1*

Cualquier desigualdad continúa siendo verdadera cuando se multiplica por un número positivo. Sabemos que *x^2≥0* para toda x y por tanto, al multiplicar por *x^2* cada lado de las desigualdad anteriores obtenemos:

*-x^2≤x^2 \sin \dfrac{1}{x}≤x^2*

O sea, *-x^2≤f(x)≤x^2*

Sabemos que *\lim_{x\to 0} x^2=0* y *\lim_{x\to 0} (-x^2)=0.*

Tomando *g(x)=-x^2* y *h(x)=x^2,* por el teorema de compresión tenemos que

$$\lim_{x\to 0} x^2 \sin \dfrac{1}{x}=0$$

Ejemplo 1 del teorema del sándwich — Gráfica de la función del ejemplo encerrada entre las gráficas de g y h.

Ejemplo 2: Encontrar *\lim_{x\to 0} u(x)* siendo *u* una función tal que:

*1-\dfrac{x^2}{4}≤u(x)≤1+\dfrac{x^2}{2}* para toda *x≠0.*

Solución: Como ocurre que *\lim_{x\to 0} \left(1-\dfrac{x^2}{4}\right)=1* y *\lim_{x\to 0} \left(1+\dfrac{x^2}{2}\right)=1,* aplicando el teorema de compresión llegamos a que: $$\lim_{x\to 0} u(x)=1$$

Ejemplo 2 del teorema del sándwich — Gráfica de las funciones del ejemplo 2

Nótese que no importa qué tan complicada sea la función u, siempre que se cumplan las condiciones del inicio, su límite en cero será igual a uno.

Bibliografía

Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.