
Propiedades de los logaritmos
En este artículo explicamos las propiedades de los logaritmos y vemos ejemplos de cómo aplicarlas para resolver problemas de simplificación y resolución de ecuaciones.
Índice
Lista de las propiedades
Las propiedades de los logaritmos son:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
- El logaritmo de un cociente es igual a la diferencia del logaritmo del numerador y del denominador.
- El logaritmo de una potencia es igual al exponente por el logaritmo de la base.
- El logaritmo en cualquier base puede expresarse como un cociente de logaritmos en otra base.
- El logaritmo de 1 en cualquier base siempre es siempre 0.
- El logaritmo de la base es siempre 1.
Desarrollaremos cada una de estas propiedades y veremos ejemplos a continuación.
Propiedades generales
Estas leyes se derivan fácilmente de la propia definición de logaritmo.
- El logaritmo de la base es igual a 1. *\log_a{a}=1*
- El logaritmo de 1 en cualquier base es 0. *\log_a{1}=0*
- Dado que el logaritmo en base *a* de *b* es el número al que se debe elevar *a* para obtener *b,* entonces: *a^{\log_a{b}}=b*
Logaritmo de la multiplicación y la división
El logaritmo de un producto es igual a la suma de los logaritmos de los factores en la misma base.
*\log_a(b\cdot c)=\log_a{b}+\log_a{c}*
Ejemplos:
*\log_2(8\cdot 16)=\log_2{8}+\log_2{16}=3+4=7*
*\log_{10}\left(100\cdot \dfrac{1}{1000}\right)=\log_{10}{100}+\log_{10}{\dfrac{1}{1000}}=2-3=-1*
El logaritmo de un cociente es igual a la resta de los logaritmos del dividendo y divisor:
*\log_a\left(\dfrac{b}{c}\right)=\log_a{b}-\log_a{c}*
Ejemplos:
*\log_6\left(\dfrac{36}{1296}\right)=\log_6{36}-\log_6{1296}=2-4=-2*
*\log_2\left(\dfrac{64}{4}\right)=\log_2{64}-\log_2{4}=6-2=4*
Suma y resta de logaritmos
De las propiedades anteriores se deduce que la suma o resta de logaritmos de la misma base se pueden escribir como el logaritmo de un producto o cociente, respectivamente.
*\log_a{b}+\log_a{c}=\log_a{b\cdot c}*
*\log_a{b}-\log_a{c}=\log_a\left(\dfrac{b}{c}\right)*
Ejemplos:
*\log_{10}{50}+\log_{10}{2}=\log_{10}(50\cdot 2)=\log_{10}{100}=2*
*\log_2{16}-\log_2{4}=\log_2\left(\dfrac{16}{4}\right)=\log_2{4}=2*
Nota: el logaritmo de la suma o resta no es igual a la suma o resta de logaritmos.
*\log_a(x+y)≠\log_a{x}+\log_a{y}*
*\log_a(x-y)≠\log_a{x}-\log_a{y}*
Logaritmo de una potencia
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.
*\log_a(b^n)=n\cdot \log_a{b}*
Ejemplos:
*\log_2(16^6)=6\cdot \log_2{16}=6\cdot 4=24*
*\log(100^{-7})=-7\cdot \log{100}=-7\cdot 2=-14*
La propiedad del logaritmo de una potencia, además de servir para simplificar expresiones logarítmicas, también es muy útil para resolver ecuaciones logarítmicas. Si la incógnita se encuentra en un exponente, podemos usar esta propiedad para "bajar" ese exponente y posteriormente despejar la incógnita.
Ejemplo: resolver *2^x=1024*
Utilizando la propiedad antes vista, podemos reescribir esta ecuación si aplicamos logaritmos de la misma base a ambos miembros. En este caso usaremos logartimos decimales.
*\log(2^x)=\log(1024)*
*x\cdot \log(2)=\log(1024)*
A partir de este punto, la incógnita ya no se encuentra en un exponente, así que podemos despejarla para encontrar su valor:
*x=\dfrac{\log(1024)}{\log(2)}*
*x=10*
Logaritmo de una raíz
El logaritmo de una raíz es igual al logaritmo del radicando dividido entre el índice de la raíz
*\log_a\sqrt[n]{b}=\dfrac{\log_a{b}}{n}*
Esta ley se deduce de la anterior, como *\sqrt[n]{b}=b^{1/n},* entonces
*\log_a(\sqrt[n]{b})=\log_a(b^{1/n})=\dfrac{1}{n}\cdot \log_a{b}=\dfrac{\log_a{b}}{n}*
Ejemplos:
*\log_3{\sqrt{243}}=\dfrac{\log_3{243}}{2}=\dfrac{5}{2}*
*\log_5{\sqrt[3]{125}}=\dfrac{\log_5{125}}{3}=\dfrac{3}{3}=1*
Cambio de base
El logaritmo de un número en una base cualquiera se puede obtener a partir del logaritmo del mismo número en otra base, dividiendo por el logaritmo de la base original en la nueva base.
*\log_a{b}=\dfrac{\log_k{b}}{\log_k{a}}* donde *k* es la nueva base
Esta propiedad es útil a la hora de calcular logaritmos con calculadoras, las cuales solo permiten calcular logaritmos naturales o decimales. Las conversiones son las siguientes:
*\log_a{b}=\dfrac{\log{b}}{\log{a}}*
*\log_a{b}=\dfrac{\ln{b}}{\ln{a}}*
Del mismo modo los logaritmos naturales y decimales se pueden determinar uno a partir del otro:
*\log{b}=\dfrac{\ln{b}}{\ln{10}}*
*\ln{b}=\dfrac{\log{b}}{\log{e}}*
Ejemplos:
*\log_2{512}=\dfrac{\log{512}}{\log{2}}=9*
*\log_5{125}=\dfrac{\ln{125}}{\ln{5}}=3*
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Leithold, L. (1994). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.








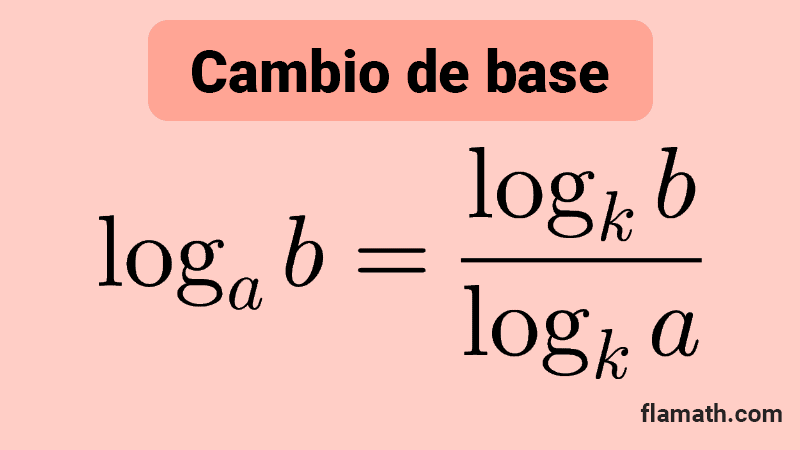
Subir

Deja una respuesta