
Lógica proposicional
En este artículo explicamos qué es la lógica proposicional y para qué sirve junto con sus conceptos básicos ejemplificados.
Índice
¿Qué es la lógica proposicional?
La lógica proposicional, también conocida como lógica de enunciados o cálculo proposicional, es una rama de la lógica matemática que estudia las proposiciones y sus combinaciones mediante conectivos lógicos.
A diferencia de la lógica de predicados, la lógica proposicional no cuantifica sobre variables ni utiliza variables libres, por lo que se considera un sistema de lógica de primer orden. La lógica proposicional permite analizar la estructura y validez de los argumentos, brindando herramientas para evaluar si un razonamiento es correcto o no basándose en el valor de verdad de sus proposiciones.
En este artículo veremos los conceptos básicos de lógica proposicional, entre los cuales tenemos:
- Proposiciones: enunciados que pueden ser evaluados como verdaderos o falsos.
- Conectivos lógicos: palabras o símbolos que se utilizan para conectar dos o más proposiciones simples y formar proposiciones compuestas.
- Tablas de verdad: herramientas que permiten evaluar el valor de verdad de proposiciones compuestas.
Proposiciones
Una proposición es una afirmación declarativa que puede ser verdadera o falsa, pero no ambas a la vez. Las proposiciones se utilizan como las unidades básicas de la lógica proposicional y se representan con las letras minúsculas p, q, r, s, etc.
Ejemplos:
- p: “El Sol es una estrella”. (Proposición verdadera).
- q: “La Tierra es plana”. (Proposición falsa).
- r: “2 + 2 = 4”. (Proposición verdadera).
- s: “El agua hierve a 90°C”. (Esta proposición es falsa).
El valor de verdad de una proposición es una de las dos posibles opciones: verdadero (V) o falso (F). Determina si la información expresada en la proposición es correcta o incorrecta en relación con la realidad.
Existen dos tipos de proposiciones:
- Proposiciones simples o atómicas: son las unidades básicas, como las que vimos en los ejemplos anteriores. No se pueden descomponer en proposiciones más pequeñas.
- Proposiciones compuestas o moleculares: se forman combinando proposiciones simples con conectivos lógicos (que veremos enseguida).
Conectivos lógicos
Los conectivos lógicos son palabras que nos permiten conectar dos o más proposiciones para formar una nueva proposición con un valor de verdad propio. Lo seis conectivos lógicos más usados son:
- Negación (¬): representa la falsedad de una proposición y se lee como "no" o "es falso que". Ejemplo: si p es “la puerta está abierta”, ¬p es “la puerta no está abierta”.
- Conjunción (∧): indica la unión de dos o más proposiciones que deben ser ciertas simultáneamente para que la expresión completa sea verdadera. Se lee como "y" o “pero”. Ejemplo: si p es “la puerta está abierta” y q es “la luz está encendida”, la proposición p ∧ q es “la puerta está abierta y la luz está encendida”.
- Disyunción (∨): representa la alternativa entre dos o más proposiciones. Al menos una de ellas debe ser cierta para que la expresión completa sea verdadera. Se lee como "o". Ejemplo: si p es “la puerta está abierta” y q es “la luz está encendida”, p∨q es “la puerta está abierta o la luz está encendida, o ambos”.
- Disyunción exclusiva (⊻): representa la alternativa entre dos o más proposiciones, pero solo una de las dos puede ser cierta para que la expresión sea verdadera. Se lee como “o ... pero no ambos”. Ejemplo: si p es “la puerta está abierta” y q es “la luz está encendida”, p⊻q es “o la puerta está abierta o la luz está encendida, pero no ambos”.
- Condicional o implicación (→): establece una relación de causa-consecuencia entre dos proposiciones. La primera proposición (antecedente) implica la segunda (consecuente). Se lee como "si... entonces". Ejemplo: si p es “la puerta está abierta” y q es “la luz está encendida”, p→q es “si la puerta está abierta, entonces la luz está encendida”.
- Bicondicional o doble implicación (↔): expresa una equivalencia lógica entre dos proposiciones. Ambas proposiciones deben ser verdaderas o falsas al mismo tiempo. Se lee como "si y solo si". Ejemplo: si p es “la puerta está abierta” y q es “la luz está encendida”, p↔q es “la puerta está abierta si y solo si la luz está encendida”.
Tablas de verdad
Las tablas de verdad son herramientas fundamentales para evaluar el valor de verdad de proposiciones compuestas. En ellas, se enumeran todas las combinaciones posibles de valores de verdad para las proposiciones atómicas (también llamadas “interpretaciones”) y se calcula el valor de verdad de la proposición compuesta en cada caso.
Ejemplo: la tabla de verdad de la proposición p ∧ q es
| p | q | p ∧ q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
La tabla indica, en su última columna, que la proposición p ∧ q es verdadera cuando p y q son verdaderas simultáneamente y es falsa en cualquier otro caso.
Contenidos recomendados:
Simbología de lógica proposicional
En la siguiente tabla se expresan los símbolos de lógica proposicional junto con su nombre y pronunciación.
| Símbolo | Nombre | Se lee |
|---|---|---|
| ¬ | Negación | no |
| ∧ | Conjunción | y |
| ∨ | Disyunción | o |
| ⊻ | Disyunción exclusiva | o (pero no ambos) |
| → | Condicional | si… entonces |
| ↔ | Bicondicional | si y sólo si |
| ∴ | Por lo tanto | por lo tanto |
Equivalencias lógicas
En lógica proposicional, dos proposiciones son equivalentes lógicamente si tienen el mismo valor de verdad en todas las posibles interpretaciones. Esto significa que las proposiciones en cuestión son intercambiables sin afectar la veracidad de un argumento.
Dos proposiciones p y q se consideran equivalencias lógicas (simbolizado como p ≡ q o también p↔q) si y sólo si sus tablas de verdad coinciden en todas las filas. Es decir, para cada combinación posible de valores de verdad de las proposiciones atómicas que componen p y q, el valor de verdad de p debe ser el mismo que el valor de verdad de q.
Las equivalencias lógicas son esenciales en la lógica matemática y la informática porque permiten simplificar proposiciones complejas y demostrar teoremas, además de permitir transformar argumentos de una forma a otra sin alterar su validez.
Algunas de las leyes de equivalencia lógica más importantes son:
- Ley de doble negación: ¬(¬p) ≡ p.
- Ley de conmutatividad de la conjunción: p ∧ q ≡ q ∧ p.
- Ley de asociatividad de la conjunción: (p ∧ q) ∧ r ≡ p ∧ (q ∧ r).
- Ley de distributiva de la conjunción sobre la disyunción: p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r).
- Ley de conmutatividad de la disyunción: p ∨ q ≡ q ∨ p.
- Ley de asociatividad de la disyunción: (p ∨ q) ∨ r ≡ p ∨ (q ∨ r).
- Ley de absorción de la conjunción en la disyunción: p ∧ (p ∨ q) ≡ p.
- Ley de absorción de la disyunción en la conjunción: p ∨ (p ∧ q) ≡ p.
- Ley de De Morgan de negación de la conjunción: ¬(p ∧ q) ≡ ¬p ∨ ¬q
- Ley de De Morgan de negación de la disyunción: ¬(p ∨ q) ≡ ¬p ∧ ¬q
Para comprobar la equivalencia lógica de dos proposiciones, se pueden construir tablas de verdad. Allí se evalúan todas las combinaciones posibles de valores de verdad para las proposiciones componentes y se comparan los resultados.
Propiedades de las equivalencias lógicas:
- Reflexividad: toda proposición es equivalente a sí misma (p ≡ p).
- Simetría: si p ≡ q, entonces q ≡ p.
- Transitividad: si p ≡ q y q ≡ r, entonces p ≡ r.
Reglas de inferencia
Las reglas de inferencia son patrones o fórmulas que permiten deducir una nueva proposición válida a partir de una o más proposiciones premisas que se consideran verdaderas. Estas reglas son fundamentales para construir argumentos lógicos válidos y razonar de manera rigurosa.
Algunas de las reglas de inferencia más comunes son:
1) Modus Ponens (MP): nos permite concluir que una proposición es verdadera si sabemos que una implicación es verdadera y su antecedente también lo es. En símbolos: si p → q y p son verdaderos, entonces q debe ser verdadera.
*\begin{array}{l} p → q \\ p \\ \hline \therefore p \end{array}*
Ejemplo:
- Si Juan estudia (p), entonces aprobará el examen (q).
- Juan estudia (p).
- Por lo tanto, Juan aprobará el examen (Q).
2) Modus Tollens (MT): nos permite concluir que el antecedente de una implicación es falso si sabemos que la implicación es verdadera y su consecuente es falso. En símbolos: si p → q es verdadera y q es falsa, entonces p debe ser falsa.
*\begin{array}{l} p → q \\ ¬q \\ \hline \therefore ¬p \end{array}*
Ejemplo:
- Si llueve (p), entonces la calle está mojada (q).
- La calle no está mojada (¬q).
- Por lo tanto, no llueve (¬p).
3) Silogismo disyuntivo (SD): nos permite concluir que una de dos proposiciones es verdadera si sabemos que una disyunción es verdadera y una de sus partes es falsa. En símbolos: si p ∨ q es verdadera y p es falsa, entonces q debe ser verdadero.
*\begin{array}{l} p ∨ q \\ ¬p \\ \hline \therefore q \end{array}*
Ejemplo:
- María está en casa (p) o está en la oficina (q).
- María no está en casa (¬p).
- Por lo tanto, María está en la oficina (q).
4) Silogismo hipotético (SH): nos permite concluir una nueva implicación a partir de dos implicaciones conectadas. En símbolos: si p → q es verdadera y q → r es verdadera, entonces p → r debe ser verdadero.
*\begin{array}{r} p → q \\ q → r \\ \hline \therefore p → r \end{array}*
Ejemplo:
- Si Pedro va al cine (p), entonces comprará palomitas (q).
- Si Pedro compra palomitas (q), entonces estará feliz (r).
- Por lo tanto, si Pedro va al cine (p), entonces estará feliz (r).
Circuitos lógicos
Los circuitos lógicos son representaciones gráficas que utilizan símbolos y diagramas para ilustrar las relaciones entre proposiciones y sus valores de verdad. Estos circuitos permiten visualizar de forma intuitiva el funcionamiento de las conectivas lógicas y cómo se determinan los valores de verdad asociándose al pasaje de corriente en un circuito eléctrico con uno o varios interruptores.
En electrónica digital, estos circuitos procesan señales binarias (0 y 1, que representan valores de verdad falso y verdadero respectivamente) para realizar operaciones lógicas. Los circuitos lógicos son fundamentales en la construcción de sistemas digitales como computadoras, dispositivos móviles y otros equipos electrónicos.
Los componentes básicos de un circuito lógico son:
1) Proposiciones (variables lógicas): representan las entradas del circuito. Cada variable lógica puede tomar uno de dos valores: 0 (falso) o 1 (verdadero).
2) Conectores lógicos (puertas lógicas): realizan operaciones lógicas sobre las variables. Las puertas lógicas básicas son:
- AND (conjunción): produce una salida de 1 solo si todas sus entradas son 1.
- OR (disyunción): produce una salida de 1 si al menos una de sus entradas es 1.
- NOT (negación): produce una salida que es la inversa de su entrada (0 se convierte en 1 y 1 se convierte en 0).
- NAND (negación de la conjunción): produce una salida de 0 solo si todas sus entradas son 1.
- NOR (negación de la disyunción): produce una salida de 0 si al menos una de sus entradas es 1.
- XOR (disyunción exclusiva): produce una salida de 1 si una y solo una de sus entradas es 1.
- XNOR (negación de la disyunción exclusiva): produce una salida de 1 si ambas entradas son iguales.
Ejemplo: el circuito lógico asociado a la proposición compuesta p ∧ (q ∨ r) es:
Aplicaciones de la lógica proposicional
La lógica proposicional tiene numerosas aplicaciones en diversas áreas debido a su capacidad para formalizar y analizar argumentos. Algunas de las principales aplicaciones de la lógica proposicional son:
- Circuitos digitales: son la base de las computadoras y otros dispositivos electrónicos y se basan en la lógica booleana, que es una aplicación directa de la lógica proposicional.
- Matemáticas: la lógica proposicional es fundamental para la axiomatización y el desarrollo de las matemáticas. Se utiliza para definir conceptos matemáticos, formular y demostrar teoremas.
- Informática: los lenguajes de programación se basan en principios de lógica proposicional para evaluar condiciones y controlar el flujo del programa.
- Filosofía: en el análisis filosófico se utiliza la lógica proposicional para estudiar la naturaleza de la verdad, el significado y la argumentación.
- Derecho: la lógica de proposiciones se utiliza en el análisis jurídico para evaluar la validez de los argumentos legales y para identificar posibles falacias en el razonamiento jurídico.
- Educación: enseñar lógica proposicional en la educación primaria y secundaria ayuda a desarrollar el pensamiento crítico y las habilidades de razonamiento lógico de los estudiantes.
Bibliografía
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.



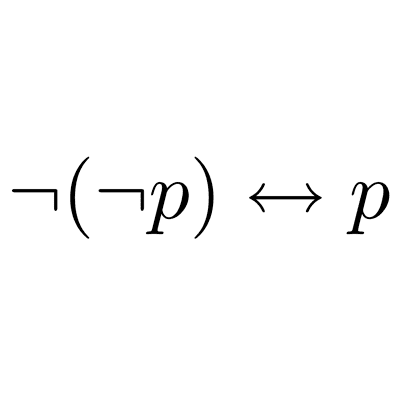
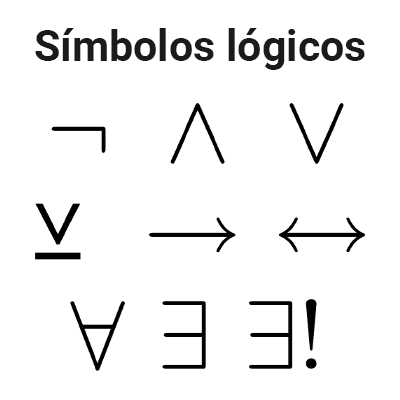
Deja una respuesta