Límite trigonométrico fundamental
En este artículo desarrollamos el límite trigonométrico fundamental con una demostración del mismo y ejemplos de aplicación para el cálculo de límites.
Índice
Límites que involucran al seno
El siguiente es conocido como el límite importante o límite fundamental:
$$\lim_{x\to 0} \dfrac{\sin x}{x}=1$$
Como la variable independiente es un ángulo, es común usar el símbolo *\theta* para representarlo. Entonces, una expresión equivalente del límite trigonométrico fundamental es:
$$\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta}=1$$
Usaremos esta simbología para la demostración.
Nota: cuando se trata de funciones, los ángulos están medidos en radianes (sistema circular) porque de esta forma son números reales. No es habitual usar otro sistema como los grados sexagesimales.
Demostración del límite fundamental
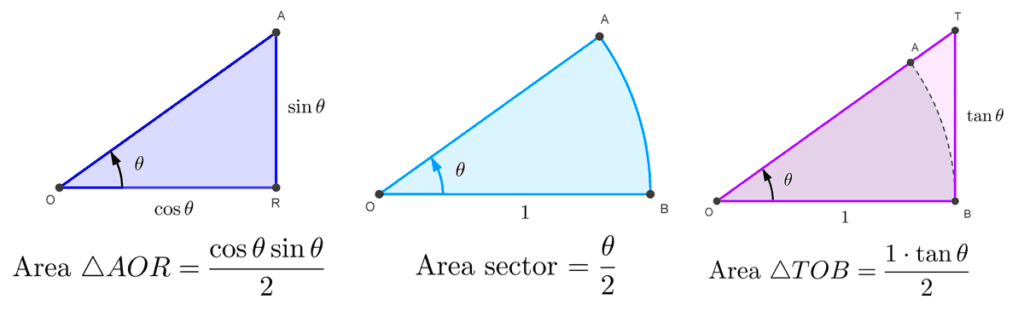
En una circunferencia de radio 1 consideramos el ángulo central *\theta.* La medida del arco AB que queda determinado sobre la circunferencia es *\theta.* En B se traza la tangente TB. De este modo, quedan conformadas tres figuras: dos triángulos y un sector circular que cumplen con la siguiente relación:
Área AOR < sector AOB < Área TOB
Las áreas correspondientes se pueden expresar en función de *\theta:*
Área del triángulo AOR *=\dfrac{1}{2}~ \text{base} \cdot \text{altura}=\dfrac{1}{2} \cos \theta \cdot \sin \theta*
Área del sector circular AOB *=\dfrac{1}{2}r^2\cdot \theta=\dfrac{1}{2}(1)^2\cdot \theta=\dfrac{1}{2}~\theta*
Área del triángulo TOB *=\dfrac{1}{2}~ \text{base} \cdot \text{altura}=\dfrac{1}{2} 1 \cdot \tan \theta=\dfrac{1}{2} \tan \theta*
En el siguiente esquema se puede ver claramente cada figura:
Reemplazando los datos obtenidos en la desigualdad inicial nos queda:
*\dfrac{1}{2} \cos \theta \cdot \sin \theta < \dfrac{1}{2}~\theta< \dfrac{1}{2}\tan \theta*
Dividiendo por *\dfrac{1}{2} \sin \theta* (que es un factor positivo si *\theta* es positivo),
*\cos \theta < \dfrac{\theta}{\sin \theta}<\dfrac{1}{\cos \theta}*
Tomando los recíprocos, las desigualdades se invierten
*\dfrac{1}{\cos \theta} > \dfrac{\sin \theta}{\theta} > \cos \theta*
Esta desigualdad vale también si cambiamos *\theta* por *-\theta,* pues en ese caso:
*\dfrac{1}{\cos (-\theta)}=\dfrac{1}{\cos \theta}~* y *~\cos (-\theta)=\cos \theta* (porque el coseno es una función par).
*\dfrac{\sin (-\theta)}{(-\theta)}=\dfrac{-\sin \theta}{(-\theta)}=\dfrac{\sin \theta}{\theta}* (porque seno y *\theta* son funciones impares).
Si hacemos tender *\theta* a *0,* *\cos \theta \to 1.* Por consiguiente, debe ser:
$$\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta}=1$$
Este resultado se puede expresar diciendo que, en el origen, *\sin \theta* es un infinitésimo equivalente a *\theta.*
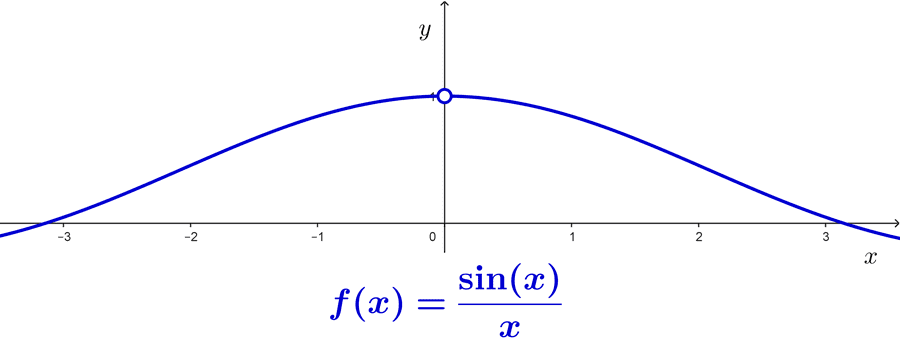
Como dijimos anteriormente, la función *f(x)=\dfrac{\sin x}{x}* es par, lo que significa que es simétrica respecto al eje y. Como los valores de *\sin x* están comprendidos entre +1 y -1, los valores de *f(x)* están comprendidos entre *y_1=\dfrac{1}{x}* e *y_2=-\dfrac{1}{x}*
Identidades trigonométricas útiles para calcular límites
Las siguientes identidades pueden ser de utilidad a la hora de obtener el valor de límites.
La tangente es igual al seno sobre coseno: *\tan(x) = \dfrac{\sin(x)}{\cos(x)}*
Identidades pitagóricas:
*\sin^2(x) + \cos^2(x) = 1*
*1 + \tan^2(x) = \sec^2(x)*
*1 + \cot^2(x) = \csc^2(x)*
Identidades recíprocas:
Cosecante: *\csc(x) = \dfrac{1}{\sin(x)}*
Secante: *\sec(x) = \dfrac{1}{\cos(x)}*
Cotangente: *\cot(x) = \dfrac{1}{\tan(x)}*
Identidades de ángulo doble:
*\sin(2x)=2\sin(x)\cos(x)*
*\cos(2x)=\cos^2(x) - \sin^2(x)*
*\tan(2x)=\dfrac{2\tan(x)}{1-\tan^2(x)}*
Identidades de suma y resta:
*\sin(a \pm b) = \sin(a)\cos(b) \pm \cos(a)\sin(b)*
*\cos(a \pm b) = \cos(a)\cos(b) \mp \sin(a)\sin(b)*
*\tan(a \pm b) = \dfrac{\tan(a) \pm \tan(b)}{1 \mp \tan(a)\tan(b)}*
Ejemplos de aplicación del límite trigonométrico fundamental
Veremos a continuación algunos ejemplos de límites que se pueden calcular utilizando el límite trigonométrico importante.
Aplicación directa
En estos problemas basta con reacomodar las expresiones utilizando propiedades algebraicas y de los límites para poder utilizar el límite fundamental.
Ejemplo 1: Obtener el valor del límite *\lim_{x\to 0} \dfrac{\sin x}{5x}*
Solución: La sustitución directa conduce a la indeterminación 0/0. Sin embargo, podemos utilizar una propiedad algebraica para reescribir la expresión y luego una propiedad de los límites para enviar la constante fuera del límite. Así:
*\lim_{x\to 0} \dfrac{\sin x}{5x}=\lim_{x\to 0} \left(\dfrac{1}{5}\cdot\dfrac{\sin x}{x}\right)*
*=\dfrac{1}{5} \lim_{x\to 0}\dfrac{\sin x}{x}*
*=\dfrac{1}{5} (1)*
*=\dfrac{1}{5}*
Ejemplo 2 : Calcular el límite *\lim_{x\to 0} \dfrac{\tan x}{x}*
Solución: La sustitución directa conduce a la indeterminación 0/0. Para resolver este problema, recurrimos a la identidad trigonométrica *\tan x=\dfrac{\sin x}{\cos x}*. Ordenando la expresión, obtenemos:
*\lim_{x\to 0} \dfrac{\tan x}{x}=\lim_{x\to 0} \left(\tan x\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{\cos x}\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{x}\cdot \dfrac{1}{\cos x}\right)*
*=\left(\lim_{x\to 0} \dfrac{\sin x}{x}\right) \left(\lim_{x\to 0}\dfrac{1}{\cos x}\right)*
*=(1)(1)*
*=1*
Aplicación por sustitución
En este tipo de problemas no es suficiente con reacomodar las expresiones, también será necesario aplicar un cambio de variable para usar el límite fundamental.
Ejemplo 3: Calcular el siguiente límite: *\lim_{x\to 0} \dfrac{\sin 2x}{5x}*
Solución: No podemos aplicar el límite fundamental directamente, pues para ello el denominador del cociente debería ser 2x. Sin embargo, podemos obtenerlo multiplicando numerador y denominador por 2/5:
*\lim_{x\to 0} \dfrac{\sin 2x}{5x}=\lim_{x\to 0} \dfrac{(2/5)\cdot \sin 2x}{(2/5)\cdot 5x}*
*=\dfrac{2}{5}\cdot \lim_{x\to 0} \dfrac{\sin 2x}{2x}*
Ahora podemos usar el límite importante, considerando *\theta=2x.* Entonces:
*\lim_{x\to 0} \dfrac{\sin 2x}{5x}=\dfrac{2}{5}\cdot \lim_{\theta \to 0} \dfrac{\sin \theta}{\theta}*
*=\dfrac{2}{5}\cdot 1*
*=\dfrac{2}{5}*
Ejemplo 4: Determinar el valor del siguiente límite *\lim_{x\to 0} \dfrac{\tan3x}{x}*
Solución: del mismo modo que en el ejemplo anterior, reescribimos la expresión para poder usar el límite fundamental:
*\lim_{x\to 0} \dfrac{\tan3x}{x}=3\left(\lim_{x\to 0} \dfrac{\tan3x}{3x}\right)*
Si hacemos *\theta=3x,* entonces cuando *x\to 0, \theta\to 0:*
*3\left(\lim_{x\to 0} \dfrac{\tan3x}{3x}\right)=3\left(\lim_{\theta \to 0} \dfrac{\tan\theta}{\theta}\right)*
*=3\left(\lim_{\theta \to 0} \dfrac{\sin\theta}{\theta \cos\theta}\right)* (porque *\tan\theta=\sin\theta/\cos\theta*)
*=3\left(\lim_{\theta \to 0} \dfrac{\sin\theta}{\theta}\right)\left(\lim_{\theta \to 0} \dfrac{1}{\cos\theta}\right)*
*=3\cdot 1\cdot \dfrac{1}{1}*
*=3*
Límites que involucran al coseno y la tangente
A partir del límite *\lim_{x\to 0} \dfrac{\sin x}{x}=1* se pueden demostrar los siguientes límites:
$$\lim_{x\to 0} \dfrac{\cos x-1}{x}=0$$
$$\lim_{x\to 0} \dfrac{\tan x}{x}=1$$
Demostraciones
1) *\lim_{x\to 0} \dfrac{\cos x-1}{x}=0 *
Multiplicando y dividiendo por el conjugado del numerador:
*\lim_{x\to 0} \dfrac{\cos x-1}{x}=\lim_{x\to 0}\left(\dfrac{\cos x-1}{x}\cdot \dfrac{\cos x+1}{\cos x+1}\right)*
*=\lim_{x\to 0}\dfrac{\cos^2x-1}{x(\cos x+1)}*
*=\lim_{x\to 0}\dfrac{-\sin^2x}{x(\cos x+1)}*
*=-\lim_{x\to 0}\left(\dfrac{\sin x}{x}\cdot \dfrac{\sin x}{\cos x+1}\right)*
*=-1\cdot \dfrac{0}{1+1}*
*=0*
Entonces: *\lim_{x\to 0} \dfrac{\cos x-1}{x}=0*
2) *\lim_{x\to 0} \dfrac{\tan x}{x}=1*
*\lim_{x\to 0} \dfrac{\tan x}{x}=\lim_{x\to 0} \left(\tan x\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{\cos x}\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{x}\cdot \dfrac{1}{\cos x}\right)*
*=\left(\lim_{x\to 0} \dfrac{\sin x}{x}\right) \left(\lim_{x\to 0}\dfrac{1}{\cos x}\right)*
*=(1)(1)*
*=1*
Entonces: *\lim_{x\to 0} \dfrac{\tan x}{x}=1*
Subir
Deja una respuesta