
Límites de funciones cuadráticas
En este artículo exploramos los límites de una función cuadrática tanto en un punto como en el más infinito y el menos infinito junto con algunos ejemplos para una mejor compresión.
Recordemos que una función cuadrática es una función real de la forma *f(x)=ax^2+bx+c* donde a, b, c son números reales y a≠0. Su dominio es el conjunto de los números reales, o sea, *D_f=\mathbb{R}.*
Índice
Límites en un punto
El límite de una función cuadrática en un punto es igual al valor de la función en dicho punto.
Sea *f(x)=ax^2+bx+c* donde *a≠0* y *D_f=\mathbb{R},* entonces:
$$\lim_{x\to p} f(x)=\lim_{x\to p} ~(ax^2+bx+c)=ap^2+bp+c$$

Ejemplos:
*\lim_{x\to 2} ~(2x^2+5x+3)=2(2)^2+5(2)+3=2\cdot 4+10+3=21*
*\lim_{x\to -1} ~(x^2+2x-3)=(-1)^2+2(-1)-3=1-2-3=-4*
*\lim_{x\to 3} ~(-4x^2-9x)=-4(3)^2-9(3)=-36-27=-63*
*\lim_{x\to -4} ~(-x^2+1)=-(-4)^2+1=-16+1=-15*
Límites en el infinito
El límite de una función cuadrática cuando la variable independiente tiende a más infinito o menos infinito es más infinito (si el coeficiente principal es positivo) o menos infinito (si el coeficiente principal es negativo). En símbolos:
$$\lim_{x\to \infty} ~(ax^2+bx+c)=+\infty~~\text{si}~~a>0$$
$$\lim_{x\to \infty} ~(ax^2+bx+c)=-\infty~~\text{si}~~a<0$$
$$\lim_{x\to -\infty} ~(ax^2+bx+c)=+\infty~~\text{si}~~a>0$$
$$\lim_{x\to -\infty} ~(ax^2+bx+c)=-\infty~~\text{si}~~a<0$$
Para valores muy grandes, el término que más aporta a la función es *ax^2.* Nótese que cuando la variable tiende a un número positivo o negativo muy grande, el hecho de estar elevada al cuadrado hace que el resultado siempre sea positivo, dejando el control del signo al número *a.*
Ejemplos:
*\lim_{x\to \infty} ~(2x^2+5x+3)=+\infty* porque *a=2>0*
*\lim_{x\to \infty} ~(-5x^2+3x-2)=-\infty* porque *a=-5<0*
*\lim_{x\to -\infty} ~(x^2-7x+1)=+\infty* porque *a=1>0*
*\lim_{x\to -\infty} ~(-7x^2+x)=-\infty* porque *a=-7<0*
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.




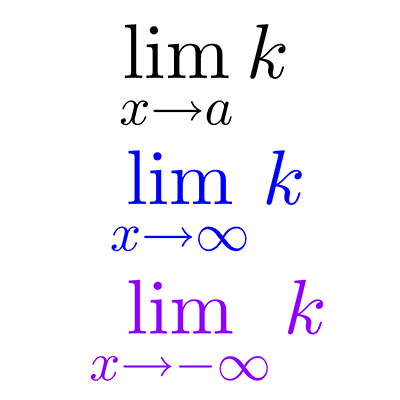

Deja una respuesta