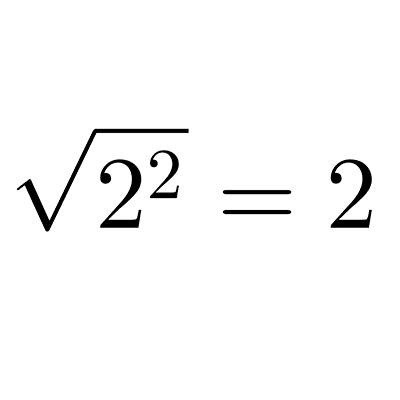
Racionalización de denominadores
Este artículo explicamos cómo racionalizar denominadores o expresiones radicales tanto si hay raíces cuadradas, cúbicas o de cualquier índice; también cuando el denominador es un binomio. Veremos ejemplos y ejercicios resueltos paso a paso.
Índice
¿Qué es racionalizar?
Racionalizar es convertir el denominador de una expresión fraccionaria en un número racional. Para esto, se remueven del mismo los radicales que aparecen. El objetivo es que la expresión resultante sea más fácil de manejar y de obtener aproximaciones.
La idea principal para conseguir esto es multiplicar numerador y denominador de la expresión por un factor que permita "subir" la raíz al numerador. Este número se conoce como factor racionalizante. Saber cuál es el factor adecuado es algo que iremos viendo a través de los distintos casos que pueden darse, tanto con monomios como binomios.
Los casos de racionalización son los siguientes:
- El denominador contiene una raíz cuadrada.
- El denominador contiene una raíz enésima (cúbica, cuarta, etc.).
- El denominador es un binomio con raíces cuadradas.
Algunas veces es necesario racionalizar el numerador de un cociente, lo que significa obtener una expresión equivalente que no tenga radicales en el numerador. El proceso es similar al empleado para racionalizar el denominador.
Caso 1: racionalizar una raíz cuadrada
Estas son expresiones de la forma *\dfrac{a}{b\sqrt{x}}.* Para racionalizar una expresión con raíz cuadrada en el denominador, multiplicamos numerador y denominador por esa misma raíz.
*\dfrac{a}{b\sqrt{x}}=\dfrac{a}{b\sqrt{x}}\cdot \dfrac{\sqrt{x}}{\sqrt{x}}=\dfrac{a\sqrt{x}}{(\sqrt{x})^2}=\dfrac{a\sqrt{x}}{x}*
En la siguiente tabla se muestran casos especiales de raíces junto con su factor racionalizante.
| Radical del denominador | Se multiplica y divide por | Nuevo denominador |
|---|---|---|
| *\sqrt{2}* | *\sqrt{2}* | *(\sqrt{2})^2=2* |
| *-\sqrt{5}* | *-\sqrt{5}* | *(-\sqrt{5})^2=5* |
| *\sqrt{y}* | *\sqrt{y}* | *(\sqrt{y})^2=|y|* |
Ejemplo 1
*\dfrac{1}{\sqrt{2}}*
En esta expresión fraccionaria, aparece una raíz cuadrada en el denominador. Para "subirla" al numerador, multiplicamos y dividimos la expresión por esa misma raíz.
*\dfrac{1}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}*
*=\dfrac{\sqrt{2}}{(\sqrt{2})^2}*
*=\dfrac{\sqrt{2}}{2}*
Ejemplo 2
*\dfrac{5}{4\sqrt{2}}*
En este caso, la raíz cuadrada aparece con un coeficiente. Esto no afecta al procedimiento, solo multiplicamos numerador y denominador por la misma raíz.
*\dfrac{5}{4\sqrt{2}}=\dfrac{5}{4\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}*
*=\dfrac{5\sqrt{2}}{4(\sqrt{2})^2}*
*=\dfrac{5\sqrt{2}}{4\cdot 2}*
*=\dfrac{5\sqrt{2}}{8}*
Ejemplo 3
*\sqrt{\dfrac{3}{7}}*
Aquí aparece la raíz cuadrada de una fracción. El objetivo es lograr una expresión donde no haya raíces en el denominador. Primero aplicamos la propiedad de las raíces para distribuir la raíz a la fracción y luego multiplicamos numerador y denominador por la raíz del denominador.
*\sqrt{\dfrac{3}{7}}=\dfrac{\sqrt{3}}{\sqrt{7}}*
*=\dfrac{\sqrt{3}}{\sqrt{7}}\cdot \dfrac{\sqrt{7}}{\sqrt{7}}*
*=\dfrac{\sqrt{3\cdot 7}}{(\sqrt{7})^2}*
*=\dfrac{\sqrt{21}}{7}*
Ejemplo 4
*\sqrt{\dfrac{3}{2x}}* con *x>0*
En este caso aparecen variables. El procedimiento a seguir es el mismo, suponiendo que todos los radicales existen.
*\sqrt{\dfrac{3}{2x}}=\dfrac{\sqrt{3}}{\sqrt{2x}}\cdot \dfrac{\sqrt{2x}}{\sqrt{2x}}*
*=\dfrac{\sqrt{3\cdot 2x}}{(\sqrt{2x})^2}*
*=\dfrac{\sqrt{6x}}{2x}*
Ejemplo 5
En el caso de tener que racionalizar un numerador, hacemos el mismo procedimiento, pero multiplicando y dividiendo por el radical del numerador.
*\dfrac{\sqrt{8}}{\sqrt{3}}=\dfrac{\sqrt{8}}{\sqrt{3}}\cdot \dfrac{\sqrt{8}}{\sqrt{8}}*
*=\dfrac{(\sqrt{8})^2}{\sqrt{3\cdot 8}}*
*=\dfrac{8}{\sqrt{24}}*
Caso 2: racionalizar una raíz de cualquier índice
Estas son expresiones de la forma *\dfrac{a}{b\sqrt[n]{x^k}},* con *k<n* y *x>0.* Para racionalizar estas expresiones, multiplicamos el numerador y denominador por *\sqrt[n]{x^{n-k}},* esto eliminará el radical del denominador:
*\dfrac{a}{b\sqrt[n]{x^k}}=\dfrac{a}{b\sqrt[n]{x^k}}\cdot \dfrac{\sqrt[n]{x^{n-k}}}{\sqrt[n]{x^{n-k}}}=\dfrac{a\sqrt[n]{x^{n-k}}}{b\sqrt[n]{x^{k+n-k}}}=\dfrac{a\sqrt[n]{x^{n-k}}}{b\sqrt[n]{x^n}}=\dfrac{a\sqrt[n]{x^{n-k}}}{bx}*
En otras palabras, se debe multiplicar y dividir por una raíz con el mismo índice pero que el exponente del radicando sea el índice menos su exponente original. La idea es que al sumar los exponentes (por producto de potencias de igual base), el resultado sea igual al índice, con lo cual la raíz se simplifica.
Algunos ejemplos de factores adecuados se dan en la siguiente tabla.
| Radical del denominador | Se multiplica y divide por | Nuevo denominador |
|---|---|---|
| *\sqrt[3]{a}* | *\sqrt[3]{a^2}* | *\sqrt[3]{a^3}=a* |
| *\sqrt[4]{a}* | *\sqrt[4]{a^3}* | *\sqrt[4]{a^4}=|a|* |
| *\sqrt[5]{a^3}* | *\sqrt[5]{a^2}* | *\sqrt[5]{a^5}=a* |
| *\sqrt[8]{a^3}* | *\sqrt[8]{a^5}* | *\sqrt[8]{a^8}=|a|* |
Nota: las barras de valor absoluto no serán necesarias si el radicando es positivo, o sea, si *a>0.*
Un caso especial es cuando en el radicando no se ve un exponente (está elevado a 1). Para racionalizar una raíz cúbica, basta con multiplicar numerador y denominador por una raíz cúbica con el radicando elevado al cuadrado. Para el caso de raíces cuartas, el factor racionalizante será una raíz cuarta con el radicando al cubo. De forma similar con las raíces de índices superiores.
Ejemplo 1
*\dfrac{1}{\sqrt[3]{7}}*
En este caso buscamos racionalizar una expresión con una raíz cúbica en el denominador. Como el radicando está elevado a 1, bastará con multiplicar numerador y denominador por *\sqrt[3]{7^2}* para eliminar el radical del denominador.
*\dfrac{1}{\sqrt[3]{7}}=\dfrac{1}{\sqrt[3]{7}}\cdot \dfrac{\sqrt[3]{7^2}}{\sqrt[3]{7^2}}*
*=\dfrac{\sqrt[3]{7^2}}{\sqrt[3]{7^3}}*
*=\dfrac{\sqrt[3]{49}}{7}*
Ejemplo 2
*\dfrac{3}{5\sqrt[4]{5}}*
En este ejemplo, la raíz del denominador es cuarta y tiene un coeficiente. Como en los casos anteriores, no es necesario hacer nada con ese coeficiente. Para racionalizar, aplicamos la fórmula que vimos, con lo cual obtenemos que el factor racionalizante es *\sqrt[4]{5^3}.*
*\dfrac{3}{5\sqrt[4]{5}}=\dfrac{3}{5\sqrt[4]{5}}\cdot \dfrac{\sqrt[4]{5^3}}{\sqrt[4]{5^3}}*
*=\dfrac{3\sqrt[4]{5^3}}{5\sqrt[4]{5^4}}*
*=\dfrac{3\sqrt[4]{5^3}}{5\cdot 5}*
*=\dfrac{3\sqrt[4]{5^3}}{25}*
Ejemplo 3
*\sqrt[3]{\dfrac{x^2}{2y^2}}* con *y≠0*
Aquí vuelven a aparecer variables. Podemos realizar los mismos pasos que antes considerando que todos los radicales existen.
*\dfrac{\sqrt[3]{x^2}}{\sqrt[3]{2y^2}}=\dfrac{\sqrt[3]{x^2}}{\sqrt[3]{2y^2}}\cdot \dfrac{\sqrt[3]{(2y^2)^2}}{\sqrt[3]{(2y^2)^2}}*
*=\dfrac{\sqrt[3]{x^2\cdot (2y^2)^2}}{\sqrt[3]{(2y^2)^3}}*
*=\dfrac{\sqrt[3]{x^2\cdot 4y^4}}{2y^2}*
*=\dfrac{\sqrt[3]{4x^2y^4}}{2y^2}*
Esta última expresión se puede seguir simplificando extrayendo una *y* del radical del numerador:
*\dfrac{\sqrt[3]{4x^2y^4}}{2y^2}=\dfrac{y\sqrt[3]{4x^2y}}{2y^2}*
*=\dfrac{\cancel{y}\sqrt[3]{4x^2y}}{2y^{\cancel{2}}}*
*=\dfrac{\sqrt[3]{4x^2y}}{2y}*
Caso 3: racionalizar un binomio
Dado un binomio a + b, su conjugado es a - b. El concepto de factor conjugado sirve para racionalizar el denominador de una fracción cuando dicho denominador es un binomio que contiene una raíz cuadrada.
Para racionalizar una expresión con denominador donde aparece un binomio con raíces cuadradas, multiplicamos y dividimos por el conjugado del denominador.
*\dfrac{a}{\sqrt{x}+\sqrt{y}}=\dfrac{a}{\sqrt{x}+\sqrt{y}}\cdot \dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-\sqrt{y}}=\dfrac{a(\sqrt{x}-\sqrt{y})}{\sqrt{x^2}-\sqrt{y^2}}=\dfrac{a(\sqrt{x}-\sqrt{y})}{x-y}*
Se está aplicando la propiedad de diferencia de cuadrados: (a + b) (a - b) = a² - b²
El mismo procedimiento funciona para expresiones de la forma *\dfrac{a}{b+\sqrt{y}},* donde solo uno de los términos es un radical. Si la o las raíces que aparecen no son cuadradas, este método no funciona, pues no se logrará desaparecer el radical.
En la siguiente tabla se muestran algunos ejemplos de los conjugados.
| Denominador | Se multiplica y divide por | Nuevo denominador |
|---|---|---|
| *\sqrt{3}+\sqrt{7}* | *\sqrt{3}-\sqrt{7}* | *3-7=-4* |
| *5-\sqrt{11}* | *5+\sqrt{11}* | *5^2-11=14* |
| *-\sqrt{2}+\sqrt{15}* | *-\sqrt{2}-\sqrt{15}* | *2-15=-13* |
| *-\sqrt{20}-6* | *-\sqrt{20}+6* | *20-6^2=-16* |
Ejemplo 1
*\dfrac{1}{6+\sqrt{5}}*
En esta fracción, el denominador es un binomio donde uno de los términos es una raíz cuadrada. Para racionalizarla, multiplicamos numerador y denominador por el conjugado de ese binomio. Es importante no cambiar todos los signos, solo el signo del segundo término.
*\dfrac{1}{6+\sqrt{5}}=\dfrac{1}{6+\sqrt{5}}\cdot \dfrac{6-\sqrt{5}}{6-\sqrt{5}}*
*=\dfrac{6-\sqrt{5}}{6^2-(\sqrt{5})^2}*
*=\dfrac{6-\sqrt{5}}{36-5}*
*=\dfrac{6-\sqrt{5}}{31}*
Ejemplo 2
*\dfrac{\sqrt{2}}{\sqrt{3}-\sqrt{2}}*
En este ejemplo, los dos términos del binomio son radicales cuadráticos. Para racionalizar, multiplicamos y dividimos por el conjugado del binomio.
*\dfrac{\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\dfrac{\sqrt{2}}{\sqrt{3}-\sqrt{2}}\cdot \dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}*
*=\dfrac{\sqrt{2}(\sqrt{3}+\sqrt{2})}{(\sqrt{3})^2-(\sqrt{2})^2}*
*=\dfrac{\sqrt{2}\sqrt{3}+\sqrt{2}\sqrt{2}}{3-2}*
*=\dfrac{\sqrt{6}+2}{1}*
*=\sqrt{6}+2*
Ejemplo 3
*\dfrac{6\sqrt{3}}{-\sqrt{x}+\sqrt{7}}*
Este ejemplo es similar al anterior, pero con variables. Como en los otros casos, procedemos de la misma forma considerando que los radicales existen.
*\dfrac{6\sqrt{3}}{-\sqrt{x}+\sqrt{7}}=\dfrac{6\sqrt{3}}{-\sqrt{x}+\sqrt{7}}\cdot \dfrac{-\sqrt{x}-\sqrt{7}}{-\sqrt{x}-\sqrt{7}}*
*=\dfrac{6\sqrt{3}(-\sqrt{x}-\sqrt{7})}{(-\sqrt{x})^2-(\sqrt{7})^2}*
*=\dfrac{-6\sqrt{3}\sqrt{x}-6\sqrt{3}\sqrt{7}}{|x|-7}*
*=\dfrac{-6\sqrt{3x}-6\sqrt{21}}{|x|-7}*
Si ocurre que *x>0,* podemos eliminar las barras del valor absoluto. Entonces, la expresión final será:
*\dfrac{-6\sqrt{3x}-6\sqrt{21}}{x-7}*
Preguntas frecuentes
¿Qué significa racionalizar un denominador?
Racionalizar un denominador se refiere al proceso de modificar la expresión algebraica de un cociente de manera que no contenga raíces en el denominador. Esto se hace para simplificar la expresión y facilitar cálculos adicionales.
¿Cómo racionalizar un denominador con raíz cuadrada?
Para racionalizar un denominador con raíz cuadrada, se multiplica tanto el numerador como el denominador de la fracción por la misma raíz cuadrada.
¿Cómo racionalizar un denominador con raíz cúbica?
Para racionalizar un denominador con raíz cúbica, se multiplica tanto el numerador como el denominador de la fracción por la misma raíz cúbica elevada al cuadrado.
¿Cómo racionalizar un denominador con un binomio?
Para racionalizar un denominador que es un binomio donde hay raíces cuadradas, se multiplica el numerador y el denominador de la fracción por el conjugado del denominador, que resulta de cambiar de signo el segundo término.
Subir
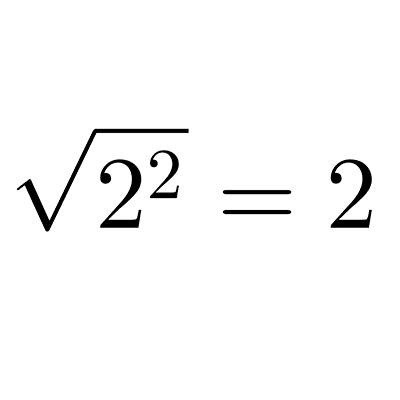
Deja una respuesta