Cómo despejar logaritmos
En este artículo explicamos cómo despejar un logaritmo tanto si la incógnita está en el argumento o en la base. También veremos cómo despejar un exponente usando logaritmos.
Índice
Incógnita dentro del logaritmo
Si la incógnita aparece dentro del argumento del logaritmo, para despejarla se pueden seguir estos pasos:
- Aislar el logaritmo: mover todos los términos que no contengan logaritmos a un lado de la ecuación.
- Exponenciar ambos lados: expresar ambos lados de la ecuación como exponentes de la base del logaritmo. Esto hará que se elimine el logaritmo.
- Resolver para la incógnita: despejar la incógnita en un lado de la ecuación.
Ejemplo 1
Resolver *\log_3 (2x)-2=2*
Solución: para despejar la x dentro del argumento, primero aislamos el logaritmo dejándolo en un miembro de la ecuación. Se puede conseguir sumando 2 a ambos miembros:
*\log_3 (2x)-2+2=2+2*
*\log_3 (2x)=4*
Ahora exponenciamos ambos lados. Como la base del logaritmo es 3, usaremos ese número como base:
*\log_3 (2x)=4*
*3^{\log_3 (2x)}=3^4*
Por propiedades de la logaritmación, queda:
*2x=3^4*
*2x=81*
Ahora podemos despejar la x:
*x=\dfrac{81}{2}*
Comprobamos que esta solución es correcta reemplazando en la ecuación original:
*\log_3 (2x)-2=2→\log_3 (2\cdot \frac{81}{2})-2=2*
*\log_3 (81)=4*
*4=4*
Ejemplo 2
Resolver la ecuación logarítmica *\log_2(2x+1)=4*
Solución: debemos despejar x dentro del logaritmo, para ello seguimos los pasos que vimos en el ejemplo anterior. El logaritmo es binario así que se usará la base 2 para despejarlo.
*\log_2(2x+1)=4*
*2^{\log_2(2x+1)}=2^4*
*2x+1=16*
*2x=15*
*x=\dfrac{15}{2}*
Comprobación:
*\log_2(2x+1)=4*
*\log_2(2\cdot \frac{15}{2}+1)=4*
*\log_2(16)=4*
*4=4*
Ejemplo 3
Resolver *\log(x)+\log(x+2)=\log(4x)*
Solución: en este caso solo aparecen logaritmos en la ecuación. En el primer miembro podemos usar la propiedad de la suma de logaritmos de igual base para reescribirlo como un producto:
*\log(x)+\log(x+2)=\log(4x)*
*\log(x(x+2))=\log(4x)*
Como tenemos una igualdad de logaritmos, los argumentos deben ser iguales:
*\log(x(x+2))=\log(4x)*
*x(x+2)=4x*
*x^2+2x=4x*
*x^2-2x=0*
*x(x-2)=0*
*x=0~~~* o *~~~x=2*
La solución *x=0* se descarta porque no existe *\log(0),* entonces, la solución es *x=2.*
Comprobación:
*\log(x)+\log(x+2)=\log(4x)*
*\log(2)+\log(2+2)=\log(4\cdot 2)*
*\log(2)+\log(4)=\log(8)*
*\log(8)=\log(8)* (por suma de logaritmos)
Ejemplo 4
Resolver la ecuación logarítmica *\ln(2)+\ln(\frac{x}{2})=1*
Solución: la suma de logaritmos del primer miembro se puede escribir como el logaritmo del producto. Para despejar el logaritmo natural, usamos de base el número e.
*\ln(2)+\ln\left(\dfrac{x}{2}\right)=1*
*\ln\left(2\cdot \dfrac{x}{2}\right)=1*
*\ln(x)=1*
*e^{\ln(x)}=e^1*
*x=e*
Ejemplo 5
Resolver *\log(5x)=2-\log(x-1)*
Solución: procedemos pasando todos los logaritmos a un miembro y aplicando propiedades para escribirlo como un solo logaritmo. Para despejar el logaritmo decimal, usamos de base el número 10.
*\log(5x)=2-\log(x-1)*
*\log(5x)+\log(x-1)=2*
*\log(5x(x-1))=2*
*10^{\log(5x(x-1))}=10^2*
*5x(x-1)=100*
*5x^2-5x-100=0*
Ahora podemos usar la fórmula resolvente para ecuaciones cuadráticas:
*x=\dfrac{+5±\sqrt{(-5)^2-4\cdot 5\cdot (-100)}}{2\cdot 5}*
*x=\dfrac{5±\sqrt{2025}}{10}*
*x=\dfrac{5±45}{10}*
*x=5~~~* o *~~~x=-4*
Tenemos dos soluciones posibles. Descartamos *x=-4* porque reemplazando en la ecuación original nos quedaría *\log(-20)=2-\log(-5),* pero no existen los logaritmos de números negativos. Por tanto, la solución es *x=5.*
Ejemplo 6
Resolver la ecuación logarítmica *\log(22-x)=-1+\log(x)*
Solución: pasamos los logaritmos a un mismo miembro y aplicamos propiedad de resta de logaritmos para reescribirlo como un cociente. Para despejar el logaritmo decimal, nuevamente usamos la base 10.
*\log(22-x)=-1+\log(x)*
*\log(22-x)-\log(x)=-1*
*\log\left(\dfrac{22-x}{x}\right)=-1*
*10^{\log(\frac{22-x}{x})}=10^{-1}*
*\dfrac{22-x}{x}=\dfrac{1}{10}*
*10(22-x)=x*
*220-10x-x=0*
*-11x=-220*
*x=\dfrac{-220}{-11}*
*x=20*
Incógnita en la base
Si la incógnita aparece dentro de la base del logaritmo, para despejarla podemos realizar los siguientes pasos:
- Aislar el logaritmo: mover todos los términos que no contengan logaritmos a un lado de la ecuación.
- Convertir a forma exponencial: usar la definición del logaritmo para reescribir la ecuación en forma exponencial, donde la incógnita aparece como base de una potencia.
- Resolver la ecuación resultante: aplicar las propiedades de las potencias para despejar la incógnita.
Ejemplo 1
Resolver la ecuación *\log_x(25)=2*
Solución: recordemos que la definición de logaritmo dice que *\log_a(b)=x* si y sólo si *a^x=b.* Es decir, la base elevada a lo que está en el segundo miembro debe ser igual al argumento. Aplicando esto a nuestra ecuación:
*\log_x(25)=2~* si y sólo si *~x^2=25*
Ahora tenemos una ecuación cuadrática que podemos despejar sencillamente:
*x^2=25*
*x=±\sqrt{25}*
*x=±5*
*x=5~~* o *~~x=-5*
Tenemos dos soluciones posibles. Descartamos *x=-5* porque la base de un logaritmo no puede ser negativa. Entonces, la solución es *x=5.*
Ejemplo 2
Resolver *\log_{x-1}(8)=3*
Solución: si escribimos el logaritmo en forma exponencial, podremos despejar la x:
*\log_{x-1}(8)=3~~* si y solo si *~~(x-1)^3=8*
*(x-1)^3=8*
*x-1=\sqrt[3]{8}*
*x-1=2*
*x=3*
Ejemplo 3
Resolver *\log_x(25)=3-\log_x(5)*
Solución: para resolver esta ecuación, aislamos en el primer miembro a los logaritmos y aplicamos propiedades para convertirlo en un solo logaritmo. Luego, pasamos a forma exponencial.
*\log_x(25)=3-\log_x(5)*
*\log_x(25)+\log_x(5)=3*
*\log_x(25\cdot 5)=3*
*\log_x(125)=3*
En forma exponencial: *x^3=125,* aplicando raíz cúbica a ambos miembros:
*x=\sqrt[3]{125}*
*x=5*
Ejemplo 4
Resolver la ecuación *\log_{2x}(3+x)=1*
Solución: en este caso, tenemos incógnita tanto en el argumento como en la base. Podemos proceder escribiendo en forma exponencial y luego resolviendo como es habitual.
*\log_{2x}(3+x)=1~~* si y sólo si *~~(2x)^1=3+x*
*(2x)^1=3+x*
*2x=3+x*
*2x-x=3*
*x=3*
Incógnita en un exponente
Si en una ecuación la incógnita está en un exponente, esta se llama ecuación exponencial, podemos hacer el despeje mediante logaritmos adecuados realizando los siguientes pasos:
- Aislar el término con incógnita: mover todos los términos que no contengan la incógnita a un lado de la ecuación.
- Aplicar logaritmo adecuado: usar logaritmos de base conveniente a ambos lados de la ecuación.
- Aplicar propiedades de logaritmos: utilizar la propiedad del logaritmo de una potencia para “bajar” el exponente con incógnita y resolver como una ecuación normal.
Ejemplo 1
Resolver la ecuación exponencial *3^x-3=240*
Solución: comenzamos dejando al término con incógnita a un lado de la ecuación.
*3^x-3=240*
*3^x=240+3*
*3^x=243*
Ahora aplicamos logaritmos a los dos lados de la ecuación. Como el exponente con la incógnita tiene base 3, usamos un logaritmo de esa base:
*3^x=243*
*\log_3(3^x)=\log_3(243)*
Por propiedad del logaritmo de una potencia, el exponente se multiplica al logaritmo. Luego, podemos despejar la x:
*\log_3(3^x)=\log_3(243)*
*x\cdot \log_3(3)=\log_3(243)*
*x=\dfrac{\log_3(243)}{\log_3(3)}*
*x=\dfrac{5}{1}*
*x=5*
Ejemplo 2
Resolver *-40+7^{3x-1}=9*
Solución: procedemos acomodando la expresión y aplicando logaritmo de base 7 para despejar la incógnita.
*-40+7^{3x-1}=9*
*7^{3x-1}=9+40*
*7^{3x-1}=49*
*\log_7 (7^{3x-1})=\log_7(49)*
*(3x-1) \log_7(7)=\log_7(49)*
*(3x-1)(1)=2*
*3x-1=2*
*3x=3*
*x=1*
Ejemplo 3
Despejar t de la ecuación *(2a)^{t/3}=5*
Solución: podemos aplicar logaritmos de base a para despejar la incógnita t.
*(2a)^{t/3}=5*
*\log_a (2a)^{t/3}=\log_a (5)*
*(t/3) \log_a (2a)=\log_a (5)*
*\dfrac{t}{3}=\dfrac{\log_a (5)}{\log_a (2a)}*
*t=3\dfrac{\log_a (5)}{\log_a (2a)}*
Aunque ya se ha logrado el despeje, la última expresión puede simplificarse aún más usando la propiedad del cambio de base:
*t=3\dfrac{\log_a (5)}{\log_a (2a)}*
*t=3\log_{2a} (5)*
Ejercicios para practicar
Ejercicio: resolver las siguientes ecuaciones.
- *\log_5(x+4)=3*
- *\log_6 (x-2)=2*
- *\log_2 (4x)=3*
- *\ln(x-1)-\ln(x+1)=8*
- *3\log_x(125)=9*
- *-2\log_x(32)=-10*
- *2^{3x}=8*
- *3^{2x}=27*
- *9^{x+2}=81*
- *e^{2x}=7*
Soluciones:
- *x=121*
- *x=38*
- *x=2*
- *x=\dfrac{e^8+1}{1-e^8}*
- *x=5*
- *x=2*
- *x=1*
- *x=\dfrac{3}{2}*
- *x=0*
- *x=\dfrac{\ln(7)}{2}≈0,973*
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Leithold, L. (1994). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.

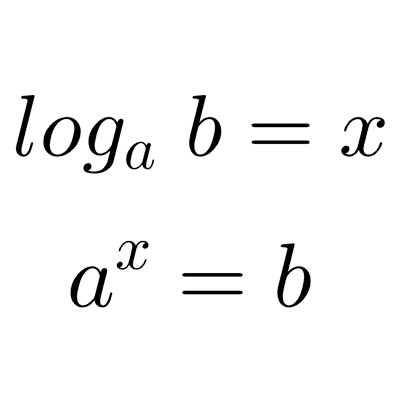



Deja una respuesta