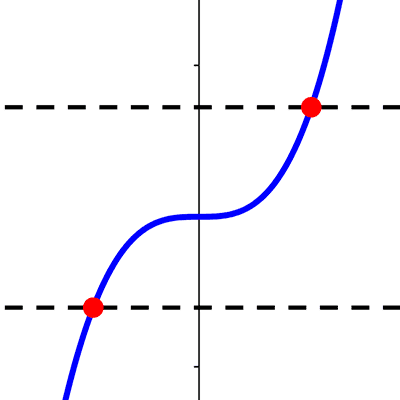
Funciones definidas por partes
En este artículo explicamos qué son las funciones definidas por partes (tramos o trozos), algunos ejemplos de ellas, cómo se grafican y cómo hallar su dominio.
Índice
Definición y ejemplos
Las funciones por partes son aquellas que están definidas por diferentes fórmulas en distintas partes de sus dominios. Estas también reciben el nombre de funciones seccionadas, segmentadas, definidas a trozos o ramas.
Ejemplo 1:
*f(x)=\begin{cases}x+1 \hspace{5mm} \text{si} \ x \leqslant 1 \\x^{2}\hspace{9.5mm} \text{si}\ x>1\end{cases}*
Recordando que una función es una regla, vemos en este caso que la regla es la siguiente: primero vea el valor de la variable independiente x. Si esta es menor o igual a 1, entonces el valor de f(x) es *x+1.* Si ocurre que x es mayor a 1, el valor de f(x) es *x^2.*
Por ejemplo, para calcular *f(0)*, como *x=0≤1,* el valor de la función será calculado con la primera fórmula: *f(0)=0+1=1*
Para hallar *f(3)*, nos fijamos en que *x=3>1*, por lo tanto usamos la segunda fórmula para hallar la imagen: *f(3)=(3)^2=9*
Si quisiéramos encontrar *f(1)*, notamos que este número se encuentra justo en el cambio de fórmulas, pero como la primera incluye a este número (por poner el símbolo de menor o igual), la usamos para calcular el valor: *f(1)=1+1=2*
Ejemplo 2:
*f(x)=\begin{cases} -x \hspace{8mm} \text{si} \ x<0 \\2x+3 \hspace{3mm} \text{si} \ 0 ≤ x ≤ 2 \\x^{3} \hspace{9.5mm} \text{si} \ x>2 \end{cases}*
Identificamos la regla de la función:
- Si la variable independiente x es menor a cero, *f(x)=-x*.
- Si x se encuentra entre 0 y 2, incluyendo a éstos, *f(x)=2x+3*
- Si x es mayor a 2, *f(x)=x^3*
Por ejemplo:
*f(-4)=-(-4)=4*
*f(1)=2(1)+1=3*
*f(4)=(4)^3=64*
Ejemplo 3: función valor absoluto
El valor absoluto de un número a, denotado *|a|* puede entenderse como la distancia de 0 hasta a en la recta real. Como las distancias son siempre cero o positivas, se cumple que *|a|≥0* para todo número a.
Si a es positivo, su valor absoluto es positivo. Si a es negativo, se cambia su signo multiplicándolo por -1, de modo que el valor absoluto resulte positivo. Si a es cero, su valor absoluto es cero.
Ejemplos:
*|2|=2*
*|-3|=3*
En general tenemos que:
*|a|=a \hspace{8mm} \text{si}~a≥0*
*|a|=-a \hspace{5mm} \text{si}~a<0*
Escribiendo estas reglas como una función a trozos, obtenemos:
*|x|=\begin{cases} x \hspace{8mm} \text{si} \ x≥0 \\-x \hspace{5mm} \text{si} \ x<0 \end{cases}*
Cómo graficar funciones por partes
Para graficar estas funciones debemos tener en cuenta que cada tramo tendrá una gráfica diferente que corresponde a la fórmula que se aplica en el mismo. Los dibujamos todos en un mismo plano cartesiano, ya que se trata de una misma función.
Ejemplo 1:
*f(x)=\begin{cases}x+1 \hspace{5mm} \text{si} \ x \leqslant 1 \\x^{2}\hspace{9.5mm} \text{si}\ x>1\end{cases}*
Hay que tomar precaución en los puntos donde cambia la regla de definición de la función. En este caso, en *x=1,* el punto sólido en *x+1* indica que el mismo pertenece a esa rama. El punto hueco de la gráfica *x^2* indica que el mismo no forma parte de esa rama. Recuerde que en ninguna función puede ocurrir que una misma x tenga dos imágenes.
Ejemplo 2:
*f(x)=\begin{cases} -x \hspace{8mm} \text{si} \ x<0 \\2x+3 \hspace{3mm} \text{si} \ 0 ≤ x ≤ 2 \\x^{3} \hspace{9.5mm} \text{si} \ x>2 \end{cases}*
Ejemplo 3:
*|x|=\begin{cases} x \hspace{8mm} \text{si} \ x≥0 \\-x \hspace{5mm} \text{si} \ x<0 \end{cases}*
Ejemplo 4:
*f(x)=\begin{cases} \sqrt{x} \hspace{6.5mm} \text{si} \ x≤4 \\1/x \hspace{6mm} \text{si} \ x>4 \end{cases}*
Ejemplo 5:
*f(x)=\begin{cases} 1 \hspace{13mm} \text{si} \ -2≤x≤0 \\x^2+1 \hspace{5mm} \text{si} \ 0< x <1 \ \\3 \hspace{13mm} \text{si} \ x=2 \\x \hspace{13mm} \text{si} \ x>3\end{cases}*
Nótese que, por la regla de la función, cuando *x=2,* *f(x)=3.* Entonces, en dicho valor, la gráfica es un solo punto. En las partes vacías del plano no se dibuja nada, ya que la regla no nos dice nada sobre ellos.
Cómo hallar el dominio de funciones por partes
Encontrar el dominio de una función consiste en reconocer todos los valores para los que ella tiene sentido. En el caso de las funciones a trozos, puede ayudarnos ver los intervalos de aplicación de una fórmula, pero no debemos olvidar que el dominio será la unión de todos los intervalos en que la función exista.
Ejemplo 1:
*f(x)=\begin{cases}x+1 \hspace{5mm} \text{si} \ x \leqslant 1 \\x^{2}\hspace{9.5mm} \text{si}\ x>1\end{cases}*
De la fórmula podemos extraer que en x=1 hay cambio de fórmula. Sin embargo, ambas fórmulas pueden existir en todo *\mathbb{R}* (por ser funciones polinómicas). Es por ello que:
*D_f=\mathbb{R}*
También podríamos haber llegado a esta conclusión mirando la gráfica.
Ejemplo 2:
*f(x)=\begin{cases} -x \hspace{8mm} \text{si} \ x<0 \\2x+3 \hspace{3mm} \text{si} \ 0 ≤ x ≤ 2 \\x^{3} \hspace{9.5mm} \text{si} \ x>2 \end{cases}*
Aunque haya tres cambios de fórmula, vemos que todas ellas son polinómicas, con lo cual no tienen restricciones en los reales. Además, como todos los valores de *\mathbb{R}* son usados en la función sin excluir ninguno, podemos concluir lo mismo que en el caso anterior:
*D_f=\mathbb{R}*
Ejemplo 3:
*f(x)=\begin{cases} \sqrt{x} \hspace{6.5mm} \text{si} \ x≤4 \\1/x \hspace{6mm} \text{si} \ x>4 \end{cases}*
Sabemos que la raíz cuadrada solo existe si x es positivo y que 1/x no existe en cero. Sin embargo, la fórmula 1/x comienza cuando x es mayor a 4, con lo cual su restricción en cero ya no importa. Aún así, sí hay restricción para la raíz. Entonces:
*D_f=[0, +∞)*
Ejemplo 4:
*f(x)=\begin{cases} 1 \hspace{13mm} \text{si} \ -2≤x≤0 \\x^2+1 \hspace{5mm} \text{si} \ 0< x <1 \ \\3 \hspace{13mm} \text{si} \ x=2 \\x \hspace{13mm} \text{si} \ x>3 \end{cases}*
Habíamos visto en la gráfica que quedaban espacios vacíos en el plano. Esto se traduce en que el dominio de la función está constituido por solo algunos números reales. Realizamos la unión de todos estos puntos y obtenemos:
*D_f=[-2,1) \cup \{2\} \cup (3, +∞)*
