
Funciones irracionales
En este artículo explicamos qué son las funciones irracionales y vemos ejemplos, aplicaciones, gráficas y análisis de casos.
Índice
¿Qué son las funciones irracionales?
Las funciones irracionales son funciones algebraicas donde la variable independiente se encuentra bajo un signo radical como una raíz cuadrada, cúbica, cuarta, etc.
Algunos ejemplos de funciones irracionales son:
*y=2+\sqrt{x+3}*
*y=\sqrt[x^2-1]-3x*
*y=x^2+\sqrt[3]{2x-5}*
*y=\sqrt{x^2-1}*
*y=1+\sqrt{4-x^2}*
*y=\sqrt{\dfrac{2x+1}{x-6}}*
*y=\dfrac{1}{\sqrt{x}+1}*
*y=\dfrac{\sqrt{x+1}}{2x}*
*y=\dfrac{x}{x\sqrt{x}-x}*
*y=\dfrac{\sqrt[4]{x-1}+2x}{7x+\sqrt{x-6}}*
Si la ecuación presenta un radical pero la variable independiente no se encuentra en el radicando, entonces no se trata de una función irracional. Por ejemplo: *y=x+\sqrt{2}* no es irracional. Las funciones potenciales de exponentes fraccionarios son también irracionales: *y=x^{m/n}* es otra forma de escribir la función *y=\sqrt[n]{x^m}.* Ejemplo: *y=x^{1/2}=\sqrt{x}.*
Las funciones irracionales se diferencian de las racionales ya que estas últimas son cocientes de funciones polinómicas donde la variable no puede estar dentro de un radicando.
Las funciones con radicales tienen diversas aplicaciones en matemáticas y otras ciencias, algunas de ellas son:
- Para calcular el radio de un círculo de área A: *r=\sqrt{\dfrac{A}{\pi}}*
- Para calcular el radio de una esfera de volumen V: *r=\sqrt[3]{\dfrac{3V}{4\pi}}*
- Para calcular la longitud L del lado de un cuadrado de área A: *L=\sqrt{A}*
- Para conocer el tiempo que tarda en tocar el suelo un objeto que se deja caer desde una determinada altura.
Al igual que con las demás funciones, con las irracionales es posible realizar operaciones como la suma, resta, multiplicación y división. Hay que prestar atención al dominio de las funciones originales para que la función resultante esté definida.
No existen reglas específicas para encontrar el dominio y el rango de una función irracional, pero se debe tener en cuenta que las raíces de índice par deben tener radicando no negativo, porque no existen raíces de índice par de números negativos en el conjunto de los números reales. En el caso de índices impares no existe esta restricción.
Ejemplos:
- La función *y=2+\sqrt{x+3}* tiene una raíz cuadrada, por lo tanto, su radicando *x+3* debe ser mayor o igual a cero: *x+3≥0 → x≥-3.* Como no existe otra restricción, el dominio es *D=[-3,+\infty).*
- En la función *y=\dfrac{\sqrt{x+1}}{2x}* ocurre algo similar a lo anterior: el radicando *x+1* debe ser no negativo, despejando se obtiene *x+1≥0 → x≥-1.* Además, hay un denominador que no puede ser cero: *2x≠0 → x≠0.* Como no hay más restricciones, el dominio es *D=[-1,0)∪(0,+\infty).*
- La función *y=\sqrt{x^2-1}* debe tener radicando no negativo, entonces: *x^2-1≥0 → x^2≥1 → |x|≥1.* A partir de esto último y por propiedad del valor absoluto se deduce que *x≥1* o *x≤-1,* por tanto, el dominio es *D=(-\infty,-1]∪[1,+\infty).*
Ejemplos y gráficas
Existen infinitas posibilidades para las gráficas de funciones irracionales, a continuación veremos algunos ejemplos y análisis de funciones con radicales.
Ejemplo 1
*y=\sqrt{x^2-1}*
Análisis de la función:
- Dominio: *(-\infty,-1]∪[1,+\infty)*
- Rango: *[0,+\infty)*
- Asíntota horizontal: no tiene.
- Asíntota vertical: no tiene.
- Raíces: *x=-1* y *x=1.*
- Intersección con el eje y: no existe.
- Intervalo de crecimiento: *(1,+\infty)*
- Intervalo de decrecimiento: *(-\infty,-1)*
- Simetría: la función es par.
- Máximo: no existe.
- Mínimos: en *x=-1* y *x=1.*
Ejemplo 2
*y=\dfrac{1}{\sqrt{x}+1}*
Análisis de la función:
- Dominio: *[0,+\infty)*
- Rango: *(0,1]*
- Asíntota horizontal: *y=0*
- Asíntota vertical: no tiene.
- Raíces: no tiene
- Intersección con el eje y: *(0, 1)*
- Intervalo de crecimiento: no tiene.
- Intervalo de decrecimiento: *(0,+\infty)*
- Simetría: la función no es par ni impar.
- Máximo: en *x=0*
- Mínimo: no tiene.
Ejemplo 3
*y=1+\sqrt{4-x^2}*
Análisis de la función:
- Dominio: *[-2,2]*
- Rango: *[1,3]*
- Asíntota horizontal: no existe.
- Asíntota vertical: no existe.
- Raíces: no tiene.
- Intersección con el eje y: *(0, 3)*
- Intervalo de crecimiento: *(-2, 0)*
- Intervalo de decrecimiento: *(0, 2)*
- Simetría: la función es par.
- Máximo: en *x=0.*
- Mínimos: en *x=-2* y *x=2.*
Ejemplo 4
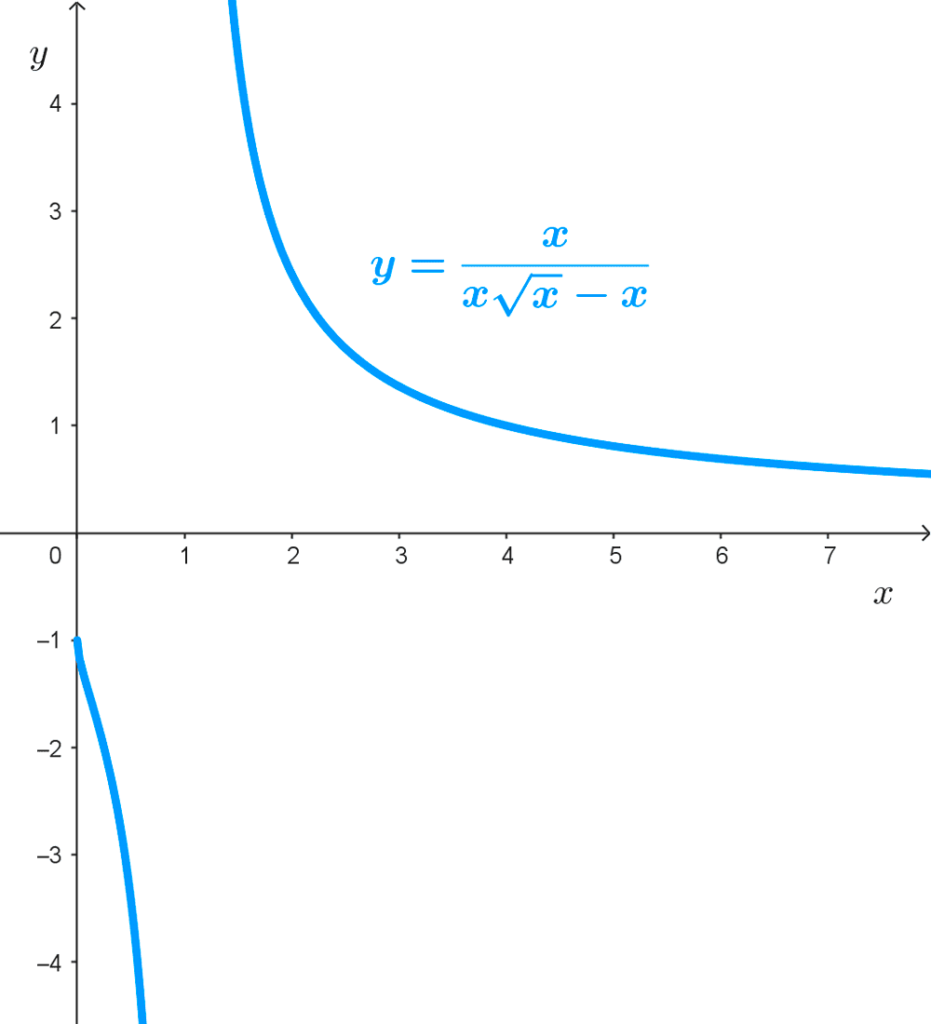
*y=\dfrac{x}{x\sqrt{x}-x}*
Análisis de la función:
- Dominio: *(0,+\infty)*
- Rango: *(-\infty,-1)∪(0,+\infty)*
- Asíntota horizontal: *x=1*
- Asíntota vertical: *y=0*
- Raíces: no tiene.
- Intersección con el eje y: no existe.
- Intervalo de crecimiento: *(0,+\infty)*
- Intervalo de decrecimiento: no existe.
- Simetría: la función no es par ni impar.
- Máximo local: en *x=0.*
- Mínimo: no existe.
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.



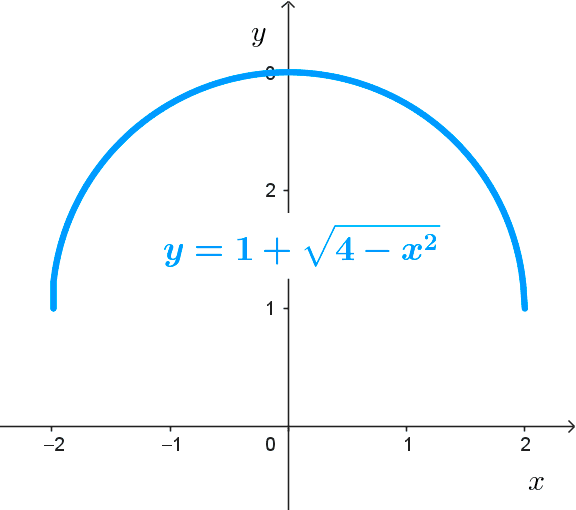


Deja una respuesta