Funciones potenciales

En este artículo explicamos qué son las funciones potenciales y vemos ejemplos, características, propiedades y gráficas de estas funciones.

Índice

¿Qué es una función potencia?

Las funciones potencia son aquellas de un solo término donde la variable aparece elevada a un exponente fijo, es decir, tienen la forma f(x)=axⁿ donde a y n son números reales. El número a se llama coeficiente.

A diferencia de las funciones exponenciales, donde la base es constante y el exponente es variable, en las funciones potenciales la base es variable y el exponente es constante. Toda función potencia es polinómica y, por tanto, algebraica.

Las funciones potencia tienen aplicaciones en numerosas disciplinas científicas y de ingeniería. Por ejemplo: en física describen fenómenos como la gravitación universal y los flujos en mecánica de fluidos, en economía modelan la oferta y demanda, así como el crecimiento económico, en ingeniería eléctrica describen relaciones en circuitos eléctricos.

Algunos ejemplos de funciones potenciales son:

Área de un círculo: *A=\pi r^2*
Volúmen de una esfera: *V=\frac{4}{3}\pi r^3*
Una función constante es una función potencial, pues si hacemos el exponente de x igual a 0, tenemos que *y=ax^0=a*
La función identidad *y=x* es una función potencia donde el exponente de la x es 1.
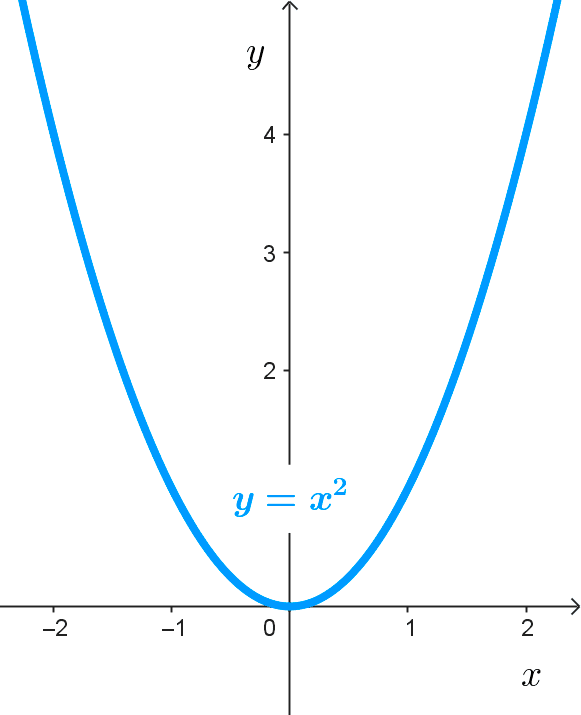
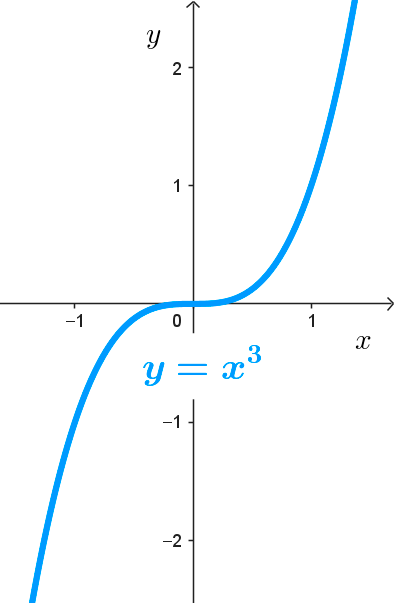
La función cuadrática *y=x^2* y la función cúbica *y=x^3* son potenciales con exponentes naturales.
La función racional *y=\dfrac{1}{x}* es potencial con exponente negativo, pues se puede escribir como *y=x^{-1}*
Con la función racional *y=\dfrac{1}{x^2}* ocurre lo mismo que en la anterior, solo que el exponente es -2: *y=x^{-2}*
Las funciones raíz cuadrada *f(x)=\sqrt{x}* y raíz cúbica *g(x)=\sqrt[3]{x}* son potenciales con exponentes fraccionarios; en particular: *f(x)=\sqrt{x}=x^{1/2}* y *g(x)=\sqrt[3]{x}=x^{1/3}*

Gráfica de la función potencial cuadrática y=x^2 — Gráfica de la función y=x²

Gráfica de la función potencial cúbica y=x^3 — Gráfica de la función y=x³

Características

Veremos a continuación las características y propiedades que comparten las funciones potencia. Nos enfocaremos más en exponentes enteros tanto positivos (números naturales) como negativos, ya que son estos los que se trabajan habitualmente.

Dominio

El dominio de una función potencia depende del valor del exponente:

Si el exponente es entero y positivo, el dominio es el conjunto de los números reales *\mathbb{R}.*
Si el exponente es entero y negativo, el dominio es el conjunto de los números reales excepto el cero.
Si el exponente es cero, el dominio es todos los números reales excepto 0.

Rango

El rango de una función potencia depende del valor del exponente:

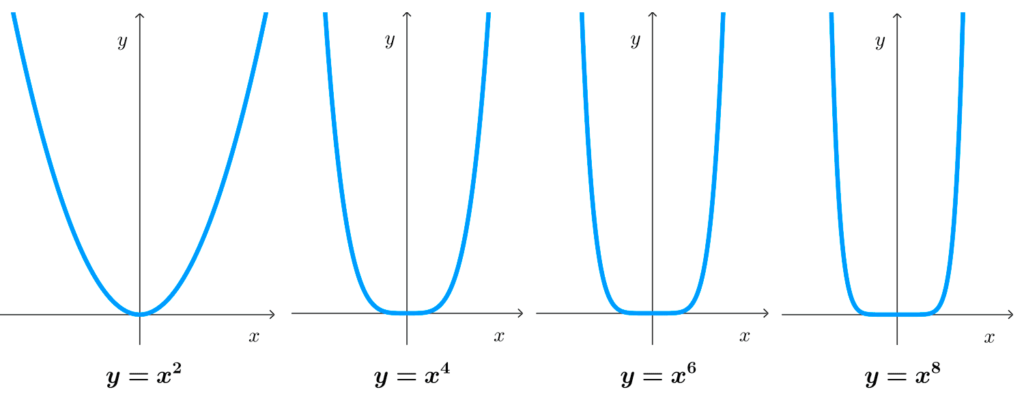
Si el exponente es entero, positivo y par, el rango son los números reales no negativos: *[0,+\infty).*
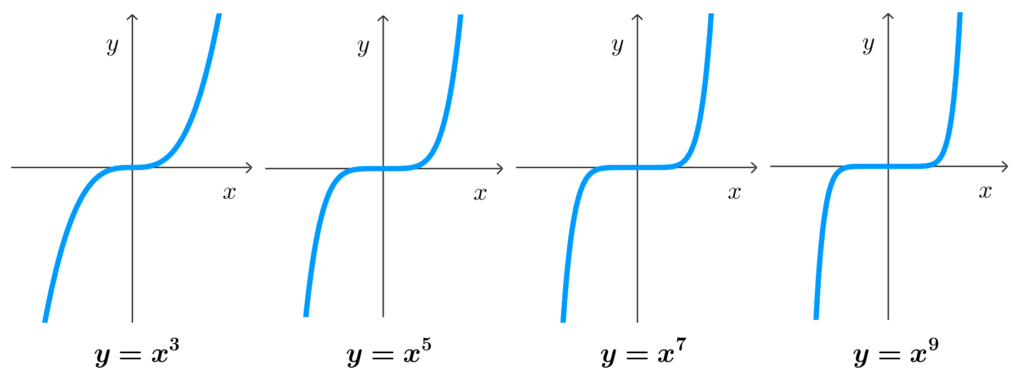
Si el exponente es entero, positivo e impar, el rango son todos los números reales.
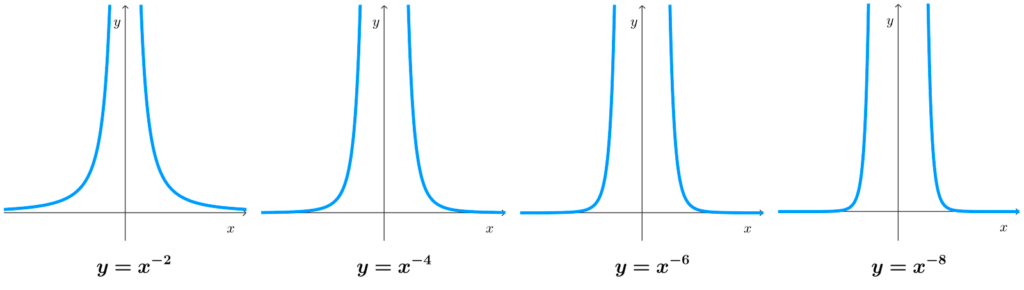
Si el exponente es entero, negativo y par, el rango son todos los números reales positivos: *(0,+\infty).*
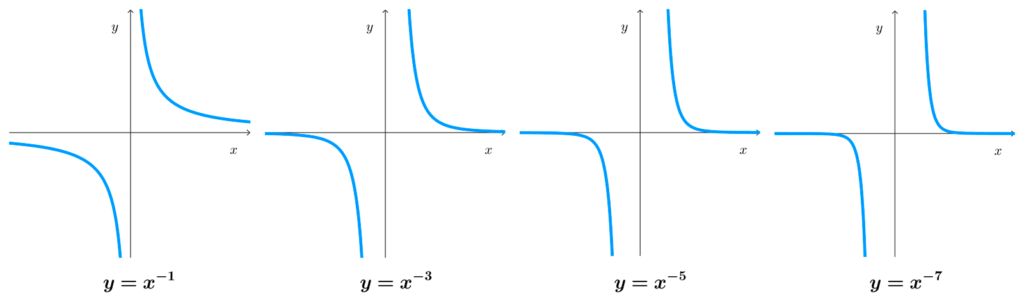
Si el exponente es entero, negativo e impar, el rango son todos los números reales excepto el cero.

Raíces e intersección con el eje y

La intersección con el eje x depende del exponente:

Si el exponente es entero positivo, la función tiene una raíz en *x=0*
Si el exponente es entero negativo, la función no tiene raíces, pues nunca corta al eje x.

La intersección con el eje y también depende del exponente:

Si el exponente es entero positivo, la gráfica corta al eje y en (0,0)
Si el exponente es entero negativo, la función nunca corta al eje y.

Simetría

Las funciones potenciales de exponentes enteros pueden ser pares o impares y esto depende de la paridad o no del exponente:

Si el exponente es par, la función potencia es par, simétrica con respecto al eje y.
Si el exponente es impar, la función potencia es impar, simétrica con respecto al origen de coordenadas.

Otros aspectos

Continuidad: las funciones potenciales son continuas en todo su dominio y describen curvas suaves.
Crecimiento y decrecimiento: las funciones potencia de exponente entero positivo impar son crecientes o decrecientes dependiendo de si el coeficiente es positivo o negativo, respectivamente. Las demás funciones tienen un intervalo donde son crecientes y otro donde son decrecientes.
Asíntotas: en las funciones potenciales de exponente positivo no existen asíntotas, pero en las de exponentes enteros negativos sí existen una asíntota vertical en x=0 y una asíntota horizontal en y=0.
Concavidad: las funciones potencia de exponente entero positivo par son cóncavas hacia arriba (convexas) si el coeficiente es positivo y cóncavas hacia abajo (o simplemente cóncavas) si el exponente es negativo. Para los exponentes enteros positivos impares, existe un intervalo de concavidad y otro de convexidad; en estos casos, existen puntos de inflexión.
Máximos y mínimos: no existen puntos máximos ni mínimos en las funciones potenciales de exponentes enteros negativos ni para positivos impares. En cambio, las funciones potencia de exponente entero positivo par tienen un máximo (si a<0) o un mínimo (si a>0) en el punto (0,0).

De la misma manera que con el resto de funciones, con las funciones potenciales se pueden efectuar operaciones elementales como sumar, restar, multiplicar y dividir. Es crucial examinar detenidamente los dominios originales para garantizar la validez de la función resultante.

Ejemplos y gráficas

Gráficas de funciones potenciales de exponentes enteros positivos (naturales) pares — Funciones potenciales de exponentes naturales pares. Nótese que la gráfica tiene forma de U y se "aplasta" más cerca del eje x a medida que el exponente crece.

Gráficas de funciones potenciales de exponentes enteros positivos (naturales) impares — Funciones potenciales de exponentes naturales impares. A partir del exponente cúbico, las gráficas de las siguientes tienen una forma similar pero más "aplastadas" cerca del eje x.

Gráficas de funciones potenciales de exponentes enteros negativos pares — Funciones potenciales de exponentes enteros negativos pares. Las gráficas se van "aplastando" más cerca del eje x y van alejándose del eje y.

Gráficas de funciones potenciales de exponentes enteros negativos impares — Funciones potenciales de exponentes enteros negativos impares. Todas las gráficas tienen similitud con la de y=x^-1 pero se van alejando del eje y.

Ejercicio para practicar

Ejercicio: determinar si las siguientes funciones son potenciales o no.

*y=2^x*
*y=x^{5,7}*
*y=\sqrt[3]{x^2}*
*y=\dfrac{1}{\sqrt{x}}*
*y=x^2+x^3+x^4*

Soluciones:

No es una función potencia, sino exponencial: la variable está en un exponente.
Es una función potencial.
Es una función potencial, puede escribirse como *y=x^{2/3}*
Es una función potencia, puede escribirse como *y=x^{-1/2}*
No es una función potencia porque hay diferentes términos con diferentes exponentes.

Preguntas frecuentes

¿Cómo saber si una función es potencial?

Para saber si una función es potencial se debe verificar que su ecuación sea el producto de una constante por la variable independiente elevada a un exponente real fijo.

¿Cuál es la diferencia entre potencial y exponencial?

En una función potencial, la base es variable y el exponente es fijo. En cambio, en una función exponencial, la base es fija y el exponente es variable.