Funciones radicales

0 - Votos: 0

En este artículo explicamos qué son las funciones radicales y vemos ejemplos, características, gráficas y aplicaciones.

Índice

¿Qué es una función radical?

Una función radical es una función algebraica cuya ecuación es una raíz cuadrada, cúbica o de otro índice y la variable independiente aparece en el radicando. Es decir, las funciones radicales tienen la forma *f(x)=a\sqrt[n]{g(x)}* donde *g(x)* es una función polinómica o racional.

Algunos ejemplos de funciones radicales son:

*y=\sqrt{x}*
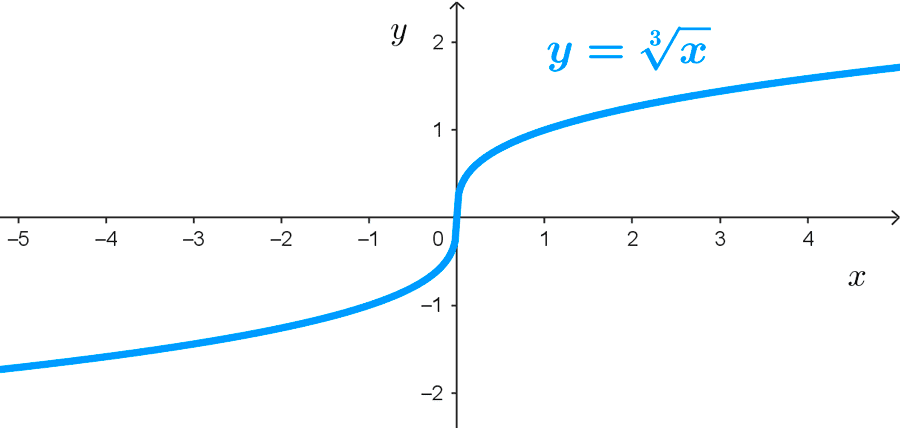
*y=\sqrt[3]{x}*
*y=\sqrt[4]{x}*
*y=\sqrt{x+1}*
*y=\sqrt{x^2-2x+4}*
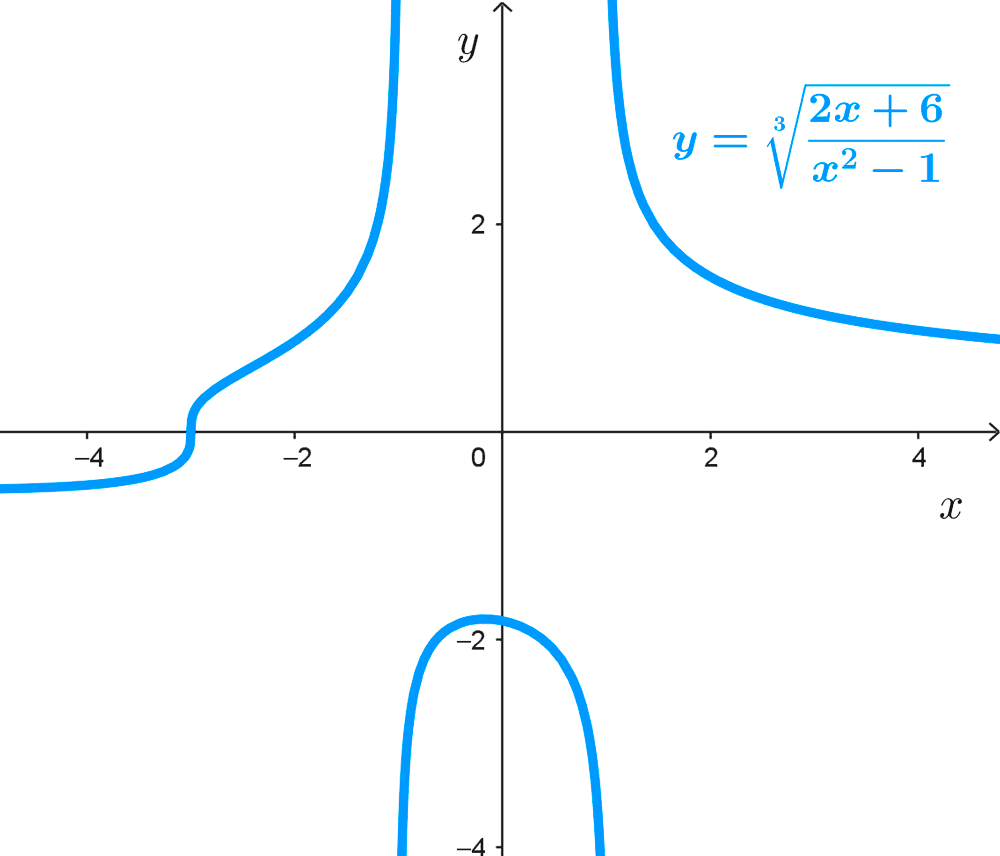
*y=\sqrt[3]{\dfrac{2x+6}{x^2-1}}*

Gráfica de la función raíz cuadrada de x — Gráfica de la función raíz cuadrada

Gráfica de la función raíz cúbica de x — Gráfica de la función raíz cúbica

Las funciones radicales tienen aplicaciones en matemática, física y otras ciencias, algunas de ellas son:

Para modelar fenómenos físicos como el movimiento de un objeto en caída libre y otros de movimiento rectilíneo uniformemente variado.
Para conocer la longitud de la hipotenusa de un triángulo rectángulo si se conocen las longitudes a y b de sus catetos: *h=\sqrt{a^2+b^2}.*
Para conocer la distancia entre dos puntos en el plano cartesiano. Si *(x_1,y_1)* y *(x_2,y_2)* son dos puntos del plano, la distancia entre ellos es *d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}.*
Para calcular el radio de un círculo dependiendo de su área A: *r=\sqrt{\dfrac{A}{\pi}}.*
En estadística, para calcular el desvío estándar, una medida de dispersión que indica cuánto se desvían los valores de una muestra respecto a la media.

Características

A continuación, desarrollamos las características y propiedades de las funciones radicales.

Dominio

Para obtener el dominio de una función radical es crucial tener en cuenta el índice de la raíz: si es par, el radicando debe ser no negativo; si es impar, el radicando puede tomar cualquier valor real.

Ejemplos:

La función raíz cuadrada *y=\sqrt{x}* tiene dominio *[0,+\infty)* porque debe ocurrir que *x≥0.*
La función raíz cúbica *y=\sqrt[3]{x}* tiene dominio *\mathbb{R}* porque x puede tomar cualquier valor sin restricción.
El dominio de la función *y=\sqrt[3]{\dfrac{2x+6}{x^2-1}}* es *\mathbb{R}-\{-1,1\}* porque x puede tomar cualquier valor real excepto *x=-1* y *x=1* porque estos anulan al denominador del radicando.

Gráfica de la función radical irracional raíz cúbica de una función racional — Gráfica de la función radical del último ejemplo

Rango

El rango de una función radical depende de su ecuación, pero para los casos básicos donde el radicando es solamente x se puede obtener el siguiente patrón:

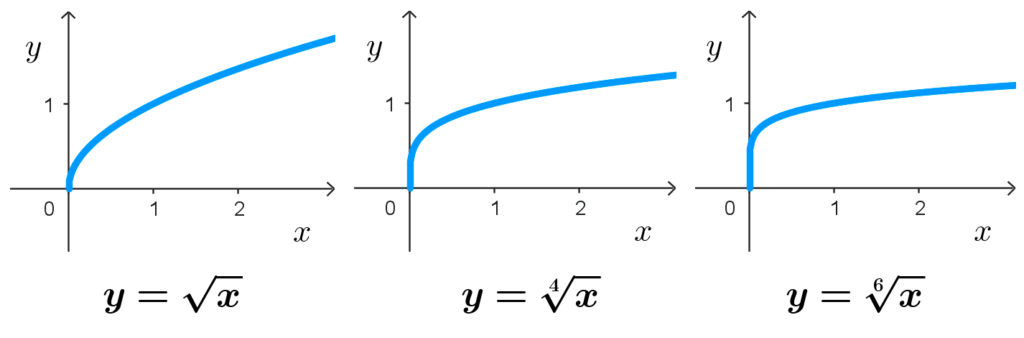
Las funciones de la forma *y=\sqrt[n]{x},* donde n es un número par, tienen por rango al conjunto de los números reales no negativos: *[0,+\infty).*
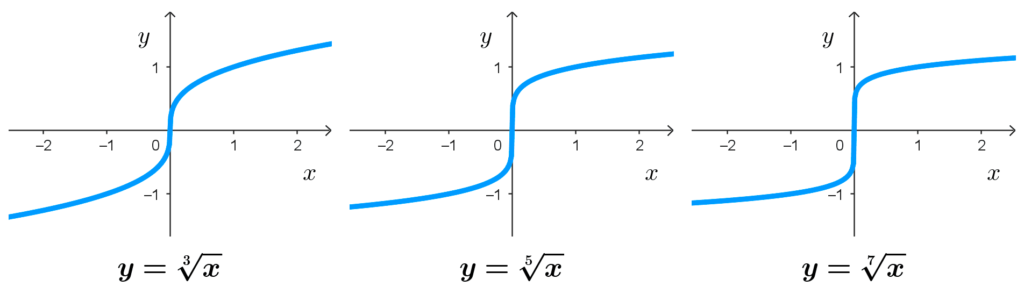
Las funciones de la forma *y=\sqrt[n]{x},* donde n es un número impar, tienen por rango al conjunto de los números reales: *\mathbb{R}.*

Por ejemplo: la función raíz cuadrada *y=\sqrt{x}* tiene como rango a *[0,+\infty)* y la función raíz quinta *y=\sqrt[5]{x}* tiene por rango a *\mathbb{R}.*

Otros aspectos

Raíces: las raíces o ceros son los valores de x donde la función es cero, para encontrarlos se debe analizar cada caso particular. En las funciones del tipo *y=\sqrt[n]{x},* el valor x=0 es la única raíz.
Intersección con el eje y: las funciones radicales pueden tener intersección con el eje y. Aquellas del tipo *y=\sqrt[n]{x}* tienen intersección en el punto *(0,0).*
Continuidad: en general, las funciones radicales son continuas en sus dominios.
Simetría: las funciones radicales de la forma *y=\sqrt[n]{x},* donde n es impar, son impares, es decir, simétricas respecto al origen de coordenadas.
Asíntotas: las funciones radicales pueden presentar asíntotas en sus gráficas. Sin embargo, si tienen la forma *y=\sqrt[n]{x}* donde n es un número natural, no existen asíntotas.
Crecimiento y decrecimiento: las funciones radicales de la forma *y=\sqrt[n]{x}* son siempre crecientes; las de la forma *y=-\sqrt[n]{x}* son siempre decrecientes. Los demás casos se deben analizar individualmente.
Al igual que con todas las funciones, con las radicales se pueden realizar operaciones matemáticas como la suma, resta, multiplicación y división. Se debe tener cuidado con el dominio de estas operaciones para asegurarse de que la función resultante tenga sentido.

Ejemplos y gráficas

A continuación veremos algunos ejemplos de gráficas que pueden servir de guía para saber cómo graficar una función radical y la forma que ésta tendrá.

Gráficas de las funciones radicales de índice par: raíz cuadrada, cuarta y sexta — Funciones radicales de índice par. Las gráficas se asemejan a la de la función raíz cuadrada y el dominio son los reales no negativos.

Gráficas de las funciones radicales de índice impar: cubica, quinta, séptima — Funciones radicales de índice impar. Las gráficas se asemejan a la de la función raíz cúbica y el dominio son todos los números reales.

Bibliografía

Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.