Formas de representar una función
En este artículo explicamos cuáles son las formas que existen para representar funciones matemáticas y cuáles son las ventajas y desventajas de cada una.
Índice
¿Cuáles son las formas de representar una función?
Existen cuatro formas de representar una función matemática:
- Verbalmente: a través de una descripción en palabras.
- Algebraicamente: por medio de una ecuación.
- Numéricamente: usando una tabla de valores.
- Visualmente: mediante un diagrama de flechas o una gráfica.
Es útil pasar de una representación a otra para obtener una mejor idea de la función. Podremos reconocer que ciertas funciones se describen de manera más natural por un método que por otro.
Representación verbal
En esta forma, se describe la relación funcional por medio de un texto con el suficiente nivel de detalle.
Ejemplos:
- “La estatura de una persona depende de su edad”
- “La población humana depende del tiempo”
- “El área de un rectángulo es base por altura”
Ventajas:
- Ofrece una forma intuitiva de describir la función sin necesidad de notación matemática compleja.
- Es fácilmente comprensible para personas no familiarizadas con la notación matemática.
- Puede proporcionar una descripción más contextualizada de la relación funcional.
Desventajas:
- Puede ser ambigua o imprecisa en comparación con la notación matemática formal.
- No es adecuada para funciones complejas que requieren una descripción detallada.
Representación algebraica
En esta forma se expresa la función como una ecuación que relaciona la variable independiente y la variable dependiente. Para la variable independiente generalmente se usa la letra x, para la dependiente la letra y o el símbolo f(x). Esta forma es muy utilizada en Cálculo, junto con la representación gráfica.
Mediante una fórmula o ecuación definimos la regla que deben cumplir dos números para estar relacionados.
Ejemplos:
*y=x^2*
*f(x)=3x+1*
*y=x^3-2*
Una forma de interpretar el primer ejemplo es: dos números x e y están relacionados por la función si ocurre que *y=x^2.* Por ejemplo, los valores *x=2, y=4* cumplen esto, por lo tanto, están relacionados. De la misma forma se pueden interpretar las demás expresiones.
Ventajas:
- Proporciona una representación precisa, específica y compacta de la relación funcional.
- Permite realizar cálculos algebraicos y manipulaciones directamente sobre la función.
- Es útil para comprender la estructura algebraica de la función, como sus raíces, puntos críticos, etc.
Desventajas:
- Puede ser difícil de interpretar para personas no familiarizadas con la notación algebraica.
- No ofrece una representación directa de la función, se debe pasar por un análisis anterior.
- En funciones complicadas, la expresión algebraica puede volverse difícil de manejar.
- No todas las funciones se pueden representar mediante una única ecuación.
Es importante aclarar que no toda expresión algebraica se trata de una función. Una desigualdad como *y<x* no define una función. Para cualquier número real x no existe un único y que sea menor que él. Por ejemplo, si *x=4,* tenemos que *y=3,* *y=2,* *y=-20* son algunos de los números que cumplen la condición *y<4.*
Tampoco la expresión *x^2+y^2=1* es una función. Por ejemplo, el valor *x=0* tiene dos correspondientes que cumplen la ecuación: *y=1* e *y=-1.* Como debe existir un único correspondiente para cada x, la ecuación no define una función.
Representación numérica
Esta también es llamada representación tabular. Se presenta una tabla donde figuran los valores de la variable independiente y a la par los valores correspondientes de variable dependiente. La tabla puede construirse de manera horizontal o vertical. Esta forma es generalmente utilizada para anotar los datos de un experimento en la vida real.
Ejemplo:
| x | y |
|---|---|
| -2 | -5 |
| -1 | -2 |
| 0 | 1 |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
Ventajas:
- Proporciona una lista completa de pares ordenados de la función.
- Es útil para calcular y comparar valores específicos de la función.
- Permite una representación discreta de la función, útil para ciertos tipos de análisis.
Desventajas:
- No se puede conocer el comportamiento de la función entre los valores dados.
- Requiere una gran cantidad de valores para representar con precisión una función compleja.
- No es eficiente para funciones continuas o suaves, con dominio infinitos o muy grandes.
Representación visual
La forma más utilizada de representación visual es la gráfica de una función, que consiste en los puntos del plano cartesiano cuyas coordenadas son las parejas de valores de entrada y salida de la función.
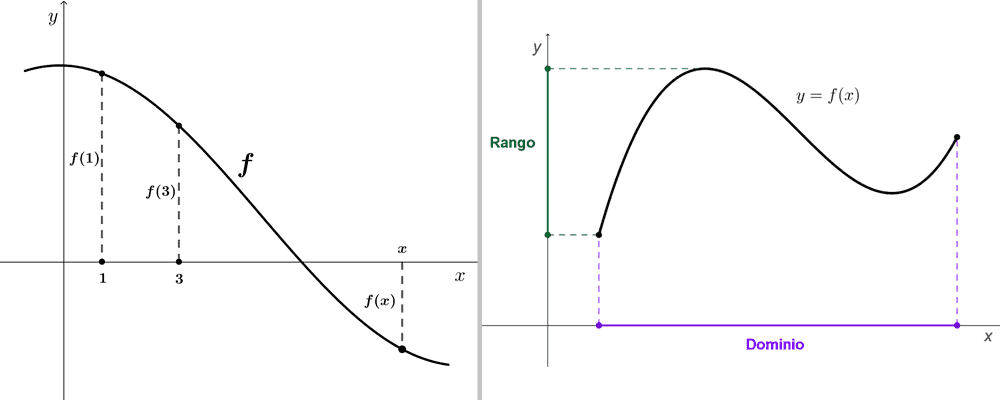
La gráfica es entonces el conjunto de puntos *(x, f(x)).* Sobre el eje horizontal (eje x) se sitúan los valores de la variable independiente y sobre el eje vertical (eje y) los valores correspondientes de la variable dependiente.
Ejemplos:
La gráfica de una función es una representación útil para saber su comportamiento. Si *(x,y)* es un punto en la gráfica, entonces *y=f(x)* es la altura de la gráfica en el punto x. Esta puede ser positiva, negativa o cero, lo cual depende del signo de f(x). También el dominio y el rango pueden verse plasmados sobre los ejes.
Para realizar la gráfica de una función puede ser útil el uso de otra forma de representación como una tabla de valores para conocer los puntos que compondrán la gráfica y luego ubicarlos. Otra forma es directamente utilizar la representación algebraica para conocer qué valor de y corresponde a cada valor de x que tomemos.
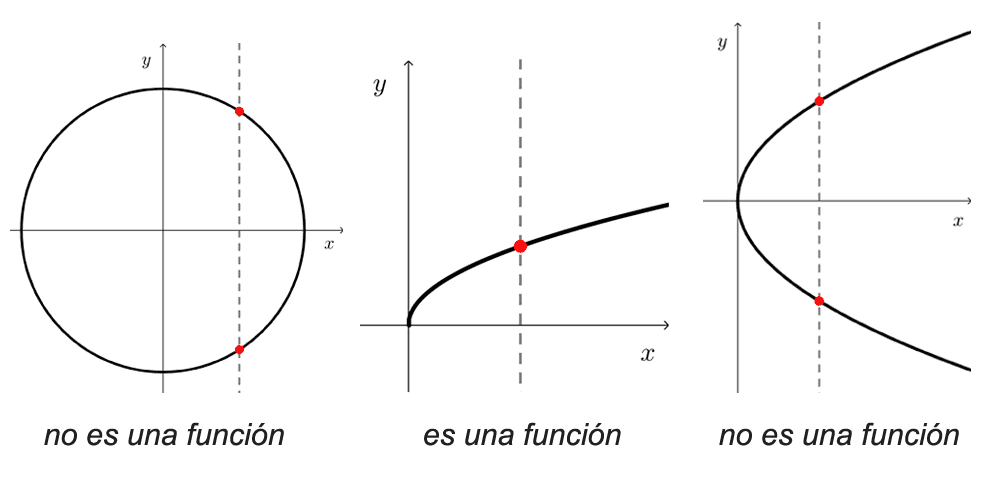
La gráfica de una función de una variable es, por lo general, una curva en el plano. Pero no cualquier curva en el plano es la gráfica de una función. Si en una curva notamos que a un mismo x le corresponde más de una y, podemos descartar que se trate de una función.
El método para reconocer esto es llamado prueba de la recta vertical, la cual nos dice que una curva en el plano cartesiano es la gráfica de una función si y sólo si ninguna recta vertical interseca la curva más de una vez.
A continuación, se presentan las ventajas y desventajas de la representación visual con la gráfica de la función.
Ventajas:
- Proporciona una representación visual clara de la función y su comportamiento.
- Permite identificar fácilmente características como pendientes, máximos, mínimos y puntos de inflexión.
- Es útil para hacer predicciones cualitativas sobre el comportamiento de la función.
Desventajas:
- La precisión de la representación depende de la escala y la calidad del gráfico.
- No siempre es posible dibujar una gráfica precisa, especialmente para funciones complicadas o con discontinuidades.
- Puede ser difícil extraer valores numéricos exactos de la gráfica.
Otra forma de representación visual de una función es mediante un diagrama de flechas, también llamado mapa de flechas o diagrama sagital. Este método muestra las relaciones entre los elementos de un conjunto de entrada y un conjunto de salida mediante flechas que van de cada elemento de entrada al elemento de salida correspondiente.

Ventajas:
- Es útil para representar relaciones entre conjuntos de entrada y salida de una función.
- Proporciona una representación visual intuitiva de cómo los elementos de un conjunto se asignan a elementos de otro conjunto.
- Puede ser útil para visualizar transformaciones y mapeos en funciones discretas.
Desventajas:
- No es adecuado para representar funciones continuas o suaves.
- Puede ser limitado en términos de expresar relaciones complejas entre conjuntos.
- Puede ser difícil de construir para funciones con un dominio o rango grandes.
- No proporciona información detallada sobre el comportamiento funcional entre los elementos mapeados.
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.
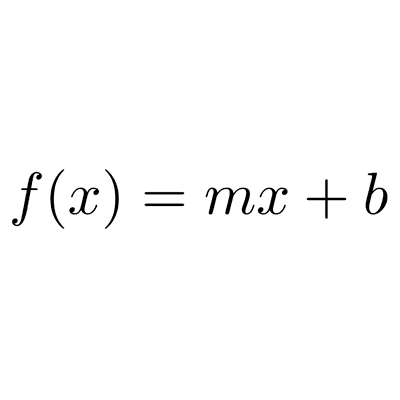

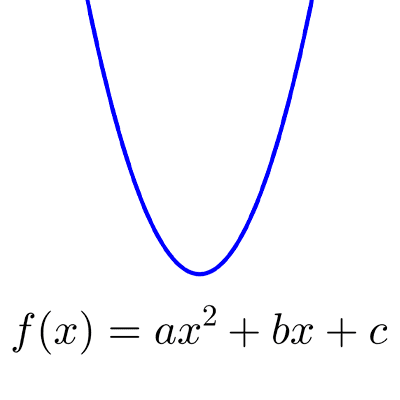
Última actualización del contenido: 15/06/2024


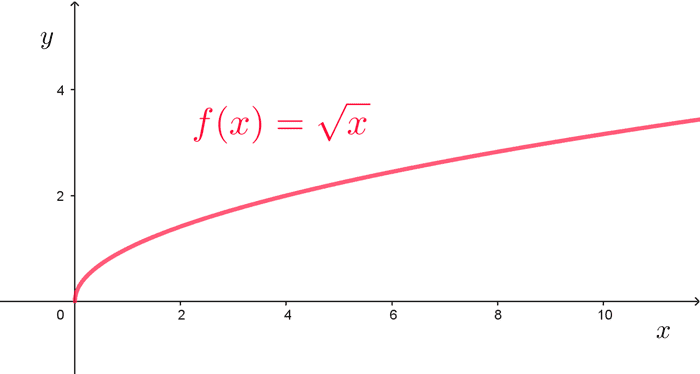
Deja una respuesta