Suma y resta de funciones

En este artículo explicamos la suma y resta de funciones reales con ejercicios resueltos paso a paso. Además, analizamos las propiedades de las operaciones.

Índice

Suma de funciones

La suma de dos funciones se define como la suma de las imágenes correspondientes. Es decir, para obtener el resultado de la suma, se deben sumar las dos expresiones algebraicas.

*(f+g)(x)=f(x)+g(x)*

El dominio de la función suma *f+g* es la intersección de los dominios de *f* y *g,* es decir, los números que son comunes a ambos dominios.

*D_{f+g}=D_f\cap D_g*

La suma de funciones conserva muchas propiedades de las funciones individuales, como simetría, periodicidad, continuidad, derivabilidad, etc. La suma de dos funciones pares resulta en una función par, la suma de funciones impares resulta en una impar.

Toda función polinómica *f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0* puede ser considerada como una suma de funciones de la forma *cx^k,* donde *c* es un número real y *k* es un número natural. La suma de dos funciones polinomiales da por resultado otra función polinomial.

Ejemplo 1

Dadas las funciones *f(x)=2x-1~* y *~g(x)=3x-5,* obtener la función *(f+g)(x)* y su dominio.

Solución: siguiendo la fórmula que vimos recién, para obtener la función suma se suman las dos ecuaciones. Entonces, escribimos las dos expresiones y simplificamos de ser posible.

*(f+g)(x)=f(x)+g(x)*

*(f+g)(x)=2x-1+3x-5*

*(f+g)(x)=5x-6*

El dominio de *f+g* es la intersección de los dominios de *f* y de *g,* como ambas funciones son polinomiales, sus dominios son el conjunto de los números reales, por lo tanto, la intersección será nuevamente ese conjunto

*D_f=\mathbb{R}~* y *~D_g=\mathbb{R}*

*D_{f+g}=D_f\cap D_g=\mathbb{R}\cap \mathbb{R}=\mathbb{R}*

Es importante notar que la imagen de la función suma de un elemento es igual a sumar las imágenes de las funciones originales por separado. Por ejemplo, *(f+g)(2)=f(2)+g(2):*

*(f+g)(2)=5(2)-6=4*

*f(2)+g(2)=2(2)-1+3(2)-5=4*

Esto se puede visualizar también a través de la gráfica.

Gráfica de la suma de dos funciones — Gráfica de la función suma f+g junto con las funciones f y g.

Ejemplo 2

Dadas las funciones *f(x)=\sqrt{x}~* y *~g(x)=\dfrac{1}{x},* obtener *(f+g)(x)* y su dominio.

Solución: primero obtenemos la expresión algebraica de la función *f+g* sumando las ecuaciones de f y de g:

*(f+g)(x)=f(x)+g(x)*

*(f+g)(x)=\sqrt{x}+\dfrac{1}{x}*

La expresión obtenida no se puede simplificar más.

*f* es una función radical y su dominio es *D_f=[0,\infty),* *g* es una función racional y su dominio son todos los reales exceptuando al cero, pues hace cero al denominador: *D_g=\mathbb{R}-\{0\},* escrito como intervalos: *D_g=(-\infty,0)\cup (0,+\infty).* El dominio de *f+g* es la intersección de los dominios de f y g:

*D_{f+g}=D_f\cap D_g=(0,+\infty)*

La función *f(x)* está definida en cero pero no en los negativos, sin embargo, la función *g(x)* no está definida en cero, pero sí en los negativos. La función suma estará definida sólo en aquellos valores en las que ambas funciones estén definidas, en este caso, en los números positivos.

Ejemplo 3

Obtener la función *(f+g)(x)* y su dominio si:

*f(x)=\dfrac{1}{x+2}~~* y *~~g(x)=\dfrac{x}{x-1}*

Solución: procedemos como siempre sumando las dos ecuaciones. En este caso, tenemos una suma de funciones racionales de diferente denominador, las sumamos como se suman fracciones algebraicas.

*(f+g)(x)=f(x)+g(x)*

*=\dfrac{1}{x+2}+\dfrac{x}{x-1}*

*=\dfrac{1(x-1)+(x+2)x}{(x+2)(x-1)}*

*=\dfrac{x-1+x^2+2x}{x^2-x+2x-2}*

*=\dfrac{x^2+3x-1}{x^2+x-2}*

El dominio de la función *f+g* lo obtenemos a partir de la intersección de los dominios de f y g:

*D_f=\mathbb{R}-\{-2\}*

*D_g=\mathbb{R}-\{1\}*

*D_{f+g}=D_f\cap D_g=\mathbb{R}-\{-2;1\}*

Como los valores excluidos de los dominios de f y g son *x=-2* y *x=1* respectivamente, del dominio de *f+g* estarán excluidos esos dos valores.

Ejemplo 4

Dadas las funciones *u(t)=\sqrt{4-t^2}~* y *~v(t)=3t+1,* obtener *(u+v)(t)* y su dominio.

Solución: el dominio de *u* es el intervalo cerrado *D_u=[-2,2],* el dominio de *v* es *D_v=\mathbb{R}.* La intersección de estos dominios es *[-2,2]* y la ecuación de la función *u+v* es:

*(u+v)(t)=\sqrt{4-t^2}+3t+1*

Ejemplo 5

Dadas las funciones *f(x)=1+\dfrac{1}{x}~* y *~g(x)=-\dfrac{1}{x},* obtener la función suma *(f+g)(x)* y su dominio.

Solución: los dominios de f y g son iguales: todos los reales excepto aquellos que hacen cero al denominador. En ambos casos, el valor que anula es cero, entonces *D_f=D_g=\mathbb{R}-\{0\}.* La intersección de estos dominios es el mismo dominio, entonces *D_{f+g}=\mathbb{R}-\{0\}.*

Para la expresión analítica, sumamos las dos ecuaciones.

*(f+g)(x)=1+\dfrac{1}{x}+\left(-\dfrac{1}{x}\right)*

*(f+g)(x)=1+\dfrac{1}{x}-\dfrac{1}{x}*

*(f+g)(x)=1*

Es importante destacar que, si hubiéramos obtenido el dominio desde la expresión final, estaríamos cometiendo un error. Al ser una función constante, su dominio es *\mathbb{R}.* Sin embargo, las funciones originales no estaban definidas en cero, esta información se pierde al realizar las operaciones. Por esto, es importante obtener el dominio de la función final a partir de la intersección de los dominios originales.

Ejemplo 6

La ganancia producida por vender *x* unidades de un producto es *G_1(x)=2x* y la ganancia por vender *x* unidades de otro producto es *G_2(x)=5x+1.* Encuentre una función que represente la ganancia total cuando se venden *x* unidades de ambos productos.

Solución: se puede obtener la ganancia total mediante la suma de las ganancias individuales, lo cual es directamente una suma de funciones. Si simbolizamos por G a la ganancia total, entonces:

*G(x)=G_1(x)+G_2(x)*

*=2x+5x+1*

*=7x+1*

En conclusión, la ganancia total por vender x unidades de los dos productos es *G(x)=7x+1.*

Propiedades

La suma de funciones cumple con una serie de propiedades operativas que veremos a continuación.

1) Conmutatividad: el orden en que se suman las funciones no altera el resultado.

*(f+g)(x)=(g+f)(x)*

2) Asociatividad: el orden en que se agrupan las funciones no altera el resultado

*((f+g)+h)(x)=(f+(g+h))(x)*

Es decir, en una suma de tres funciones, es igual sumar la primera con la segunda y el resultado sumarlo a la tercera, que sumar la segunda y la tercera y el resultado sumarlo con la primera.

3) Elemento neutro: existe una función que al ser sumada a otra no altera el valor de esta última. Esta es la función constante *g(x)=0,* pues, para cualquier función *f,* se cumple que *f(x)+0=f(x).*

4) Elemento simétrico: para cada función, existe otra que al ser sumadas producen resultado 0. Para una función *f(x),* su simétrica es *-f(x),* es decir, su opuesta. Por ejemplo, para *f(x)=3x,* su opuesta es *g(x)=-3x.*

Resta de funciones

La resta de dos funciones se define como la resta de las imágenes correspondientes. Es decir, para obtener el resultado de la resta, se deben restar las dos expresiones algebraicas.

*(f-g)(x)=f(x)-g(x)*

El dominio de la función resta *f-g* es la intersección de los dominios de *f* y *g,* es decir, los números que están en ambos dominios.

*D_{f-g}=D_f\cap D_g*

La resta, al igual que la suma, conserva muchas propiedades de las funciones individuales, como simetría, periodicidad, continuidad, derivabilidad, etc. La resta de dos funciones pares resulta en una función par, la resta de funciones impares resulta en una impar.

Ejemplo 1

Dadas las funciones *f(x)=3x^2+6~* y *~g(x)=-x^2+2x-1,* obtener *(f-g)(x)* y su dominio.

Solución: las funciones f y g son polinómicas, por tanto, tienen dominio *\mathbb{R},* la intersección entonces será el mismo conjunto, por lo cual *D_{f-g}=\mathbb{R}.* Para obtener la ecuación, restamos las dos ecuaciones en el orden que se nos pide:

*(f-g)(x)=f(x)-g(x)*

*=3x^2+6-[-x^2+2x-1]*

*=3x^2+6+x^2-2x+1*

*=4x^2-2x+7*

Ejemplo 2

Sean *f(x)=\sqrt{x-2}~* y *~g(x)=\sqrt{9-x^2},* obtener la función resta *(f-g)(x)* y su dominio.

Solución: el dominio de f es *D_f=[2,+\infty)* y el dominio de g es *D_g=[-3,3].* El dominio de *f-g* es la intersección de los dominios de f y de g, por tanto:

*D_{f-g}=[2,+\infty)\cap [-3,3]=[2,3]*

Porque el intervalo *[2,3]* es el único en el que ambas funciones están definidas al mismo tiempo. Para obtener la expresión algebraica, restamos las funciones en el orden que se nos pide:

*(f-g)(x)=\sqrt{x-2}-\sqrt{9-x^2}*

Podemos probar que nuestro análisis del dominio fue correcto revisando la gráfica, pues se ve que la función *f-g* solo existe en el intervalo *[2,3].*

Gráfica de una resta de funciones reales — Gráfica de la función resta. Nótese que la función solo existe para los valores de x del intervalo [2,3].

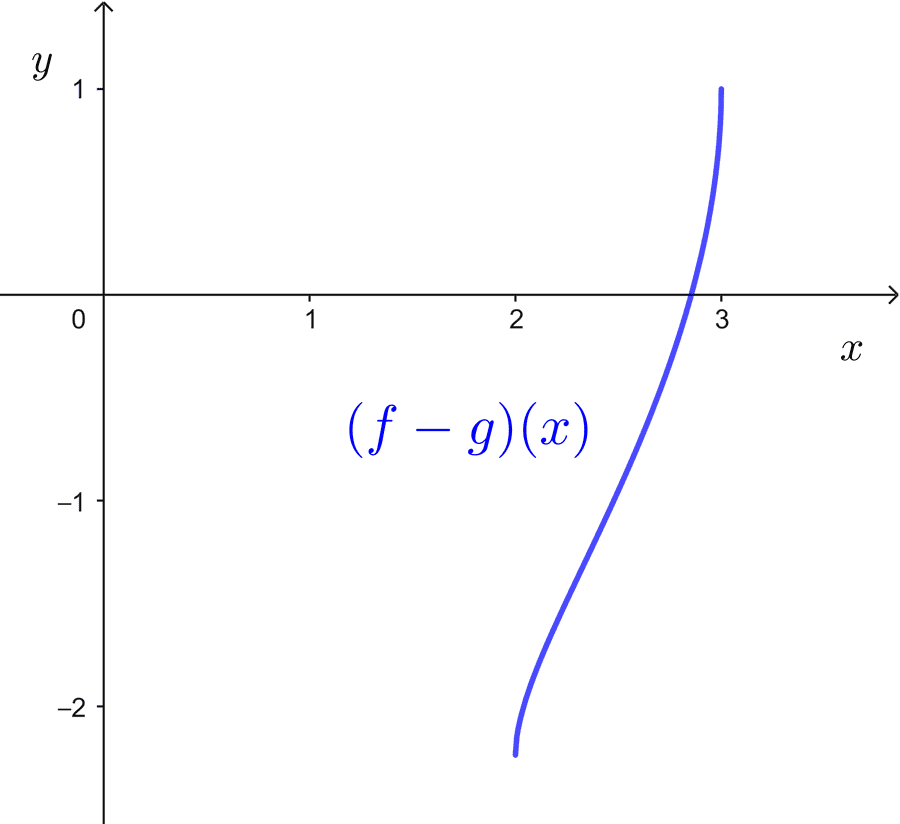
Ejemplo 3

Obtener *(f-g)(x)* y su dominio si:

*f(x)=\dfrac{2x+3}{3x-2}~~* y *~~g(x)=\dfrac{4x}{3x-2}*

Solución: los dominios de f y g son iguales: *\mathbb{R}-\{3/2\},* porque ambas son funciones racionales y el valor *3/2* anula a sus denominadores. Como la intersección de dos dominios iguales es el mismo dominio, entonces *D_{f-g}=\mathbb{R}-\{3/2\}.*

Para obtener la ecuación, restamos las dos ecuaciones. Se trata de una resta de funciones racionales de igual denominador, con lo cual procedemos como sabemos:

*(f-g)(x)=\dfrac{2x+3}{3x-2}-\dfrac{4x}{3x-2}*

*=\dfrac{2x+3-4x}{3x-2}*

*=\dfrac{-2x+3}{3x-2}*

Ejemplo 4

Dadas las funciones *u(x)=\dfrac{\cos(x)}{x-1}~* y *~v(x)=x-7,* obtener la función resta *(u-v)(x)* y su dominio.

Solución: la función *u(x)* es cociente de una función trigonométrica y una lineal. El dominio del numerador y el denominador es *\mathbb{R},* pero el denominador no puede ser cero, como esto ocurre *x=1,* ese valor queda excluido del dominio: *D_u=\mathbb{R}-\{1\}.* La función *v(x)* es polinómica, por lo cual su dominio es *\mathbb{R}.*

El dominio de *(u-v)(x)* es la intersección de los dominios de *u(x)* y *v(x).* Como el único valor que no comparten es *x=1,* este quedará excluido:

*D_{u-v}=\mathbb{R}-\{1\}*

Para obtener la fórmula de la función final, restamos las dos expresiones en el orden que se nos indica:

*(u-v)(x)=u(x)-v(x)*

*=\dfrac{\cos(x)}{x-1}-(x-7)*

*=\dfrac{\cos(x)}{x-1}-x+7*

Ejemplo 5

En un negocio, el ingreso obtenido por *x* unidades producidas de un producto está dado por la función *I(x)=2x^2+9x+2,* por otro lado, el costo de producir *x* unidades del producto está dado por la función *C(x)=6x^2-x.* Se pide obtener una función que represente la ganancia al producir *x* unidades.

Solución: la función de ganancia o de rentabilidad es lo que le queda al negocio luego de quitar los gastos de los ingresos, o sea, para obtener la función en este caso habrá que restar estas funciones. Simbolizamos por G a la función de ganancia.

*G(x)=I(x)-C(x)*

*=2x^2+9x+2-(6x^2-x)*

*=2x^2+9x+2-6x^2+x*

*=-4x^2+10x+2*

Entonces, la ganancia obtenida por producir *x* unidades del producto es *G(x)=-4x^2+10x+2.*