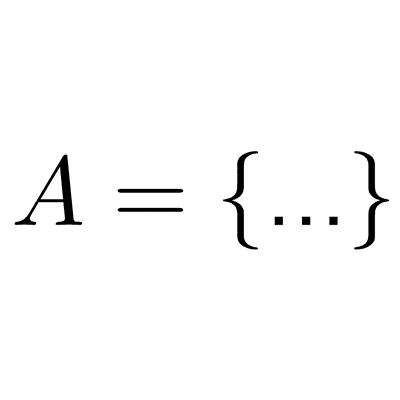
Teoría de conjuntos
En este artículo desarrollaremos los conceptos más importantes de la teoría de conjuntos que sirven de base para diversas áreas de estudio de la matemática.
Índice
¿Qué es la teoría de conjuntos?
La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades y relaciones de conjuntos, que son colecciones bien definidas de objetos. Estos conjuntos pueden contener números, letras, funciones, u otros conjuntos, dependiendo del contexto.
La teoría de conjuntos fue desarrollada a fines del siglo XIX por matemáticos como Georg Cantor y Richard Dedekind y proporciona un marco formal para la construcción de otras estructuras matemáticas y es utilizada extensamente en prácticamente todos los campos de las matemáticas, así como en la lógica y la informática.
Conceptos básicos
Los conceptos fundamentales de la teoría de conjuntos son los de conjunto, elemento y pertenencia. Sobre la base de ellos se definen la cardinalidad, las relaciones de inclusión, la igualdad de conjuntos y las demás operaciones.
Conjunto
Un conjunto es una colección de objetos bien definidos y diferenciados entre sí. Estos objetos pueden ser concretos (números, letras) o abstractos (ideas, conceptos).
Los conjuntos se denotan con letras mayúsculas A, B, C, etc. Los elementos se escriben dentro de llaves {}, separados por comas.
Ejemplos:
- A = {1, 2, 3}
- B = {a, b, c}
- C = {rojo, verde, azul}
Elemento
Un elemento es un objeto que forma parte de un conjunto. Puede ser cualquier cosa, como un número, una letra, una persona, un animal, un objeto físico o incluso un concepto abstracto.
Dos elementos iguales en un mismo conjunto se consideran como uno solo. Además, no importa en qué orden se escriban los elementos, el conjunto sigue siendo el mismo.
Ejemplos:
- El conjunto A = {1, 2, 3} tiene tres elementos: el número 1, el número 2 y el número 3.
- El conjunto B = {a, b, c} tiene tres elementos: la letra "a", la letra "b" y la letra "c".
- El conjunto C = {rojo, verde, azul} tiene tres elementos: el color rojo, el color verde y el color azul.
Pertenencia
La pertenencia es la relación que tiene un elemento con un conjunto, pudiendo formar parte de él o no. Para indicar que el elemento pertenece al conjunto, se usa el símbolo ∈; caso contrario se usa el símbolo ∉.
Ejemplos:
- 1 ∈ A (el número 1 pertenece al conjunto A)
- c ∈ B (la letra "c" pertenece al conjunto B)
- rojo ∈ C (el color rojo pertenece al conjunto C)
- 4 ∉ A (el número 4 no pertenece al conjunto A)
- d ∉ B (la letra "d" no pertenece al conjunto B)
Cardinalidad
La cardinalidad de un conjunto es una medida que indica cuántos elementos tiene ese conjunto. En otras palabras, es el número de elementos distintos contenidos en el conjunto. El cardinal de un conjunto A se simboliza por Card(A) o |A|.
Ejemplos:
- El cardinal del conjunto B = {a, b, c} es |B|=3, porque tiene tres elementos.
- El cardinal del conjunto D = {1, 2, e, f, g} es |D|=5, porque tiene cinco elementos.
La cardinalidad de un conjunto puede ser finita o infinita. En conjuntos finitos, como los ejemplos anteriores, la cardinalidad es simplemente el número de elementos que contiene el conjunto. En conjuntos infinitos, como el de todos los números naturales (1, 2, 3, 4, ...), la cardinalidad es infinita y se expresa utilizando símbolos especiales, como ℵ₀ (aleph-cero).
Igualdad de conjuntos
Dos conjuntos son iguales si tienen exactamente los mismos elementos, sin importar el orden en que estén escritos.
Ejemplos:
- A = {1, 2, 3} y E = {3, 1, 2} son conjuntos iguales.
- C = {rojo, verde, azul} y F = {rojo, azul, verde} son conjuntos iguales.
- B = {a, b, c} y G={a, b, c, d} no son conjuntos iguales, porque no tienen los mismos elementos.
Inclusión de conjuntos
Si todo elemento de un conjunto A es también elemento de un conjunto B, entonces se dice que A está incluido en B, o que A es un subconjunto de B. Simbólicamente se escribe A⊆B.
*A\subseteq B* si y sólo si *\forall x : (x\in A\rightarrow x\in B)*
Si al menos un elemento de A no está dentro de B, se dice que A no es subconjunto de B y se escribe A⊈B. Si ocurre que todo elemento de A está en B, pero B tiene algún elemento que no está en A, se dice que A es un subconjunto propio de B y se simboliza como A⊂B.
Ejemplos:
- A = {1, 2} es un subconjunto de B = {1, 2, 3, 4, 5}, porque todo elemento de A es también elemento de B: A⊆B. También se cumple que A⊂B, porque B tiene elementos que no están en A.
- C = {rojo, verde} es un subconjunto de D = {rojo, verde, azul}, o sea, C ⊆ D.
Operaciones entre conjuntos
Existen diversas operaciones que pueden realizarse entre dos o más conjuntos, también llamadas álgebra de conjuntos, ellas son:
- Unión: la unión de dos conjuntos A y B es el conjunto que contiene todos los elementos que están en A o en B o en ambos. Se denota por A ∪ B.
- Intersección: la intersección de dos conjuntos A y B es el conjunto que contiene todos los elementos que están en A y en B. Se denota por A ∩ B.
- Diferencia: la diferencia de dos conjuntos A y B es el conjunto que contiene todos los elementos que están en A pero no en B. Se denota por A-B.
- Diferencia simétrica: se llama diferencia simétrica entre dos conjuntos A y B al conjunto formado por los elementos de A que no pertenecen a B y los elementos de B que no pertenecen a A, es decir, aquellos elementos que pertenecen exclusivamente a uno de los conjuntos. Se denota por A Δ B.
- Complementación: se llama complemento de un conjunto A al conjunto A' compuesto por todos los elementos del conjunto universal U que no están en A. El conjunto universal es aquel que contiene todos los elementos relevantes para el contexto particular de estudio.
Tipos de conjuntos
En teoría de conjuntos, existen varios tipos de conjuntos, algunos de los cuales son:
- Conjunto finito: es un conjunto que tiene un número finito de elementos.
- Conjunto infinito: es un conjunto que tiene un número infinito de elementos.
- Conjunto vacío: es el conjunto que no tiene ningún elemento. Se denota por Ø.
- Conjunto unitario: es un conjunto que contiene exactamente un elemento.
- Conjunto universal: es un conjunto que contiene a todos los elementos relevantes de un contexto dado. Se denota típicamente como U.
- Conjunto de partes: el conjunto de partes de A, denotado como P(A), es el conjunto que contiene todos los subconjuntos posibles de A, incluyendo el conjunto vacío y A mismo.
Algunos conjuntos especiales que pueden destacarse son los conjuntos numéricos, los cuales contienen números con ciertas propiedades comunes: naturales (N), enteros (Z), racionales (Q), irracionales (I), reales (R), complejos (C).
Diagramas de Venn
Los conjuntos suelen representarse gráficamente mediante los llamados diagramas de Venn. Estos diagramas son figuras planas cerradas; normalmente, el conjunto universal se representa por el interior de un rectángulo y los otros conjuntos mediante globos dentro del rectángulo. Dentro de estas figuras se ubican a los elementos correspondientes.
Por ejemplo, para los conjuntos A = {a, b, c} y B = {e, f}, el diagrama de Venn es el siguiente:
Simbología
En las siguientes tablas se mostrará toda la simbología necesaria para trabajar en teoría de conjuntos junto con su significado.
Simbología básica de conjuntos y sus operaciones
| Símbolo | Significado |
|---|---|
| { } | Conjunto: colección de objetos bien definidos. |
| a ∈ A | El elemento a pertenece al conjunto A. |
| b ∉ A | El elemento b no pertenece al conjunto A. |
| |A| | Cardinalidad del conjunto A. |
| A = B | Los conjuntos A y B son iguales. |
| A ⊆ B | A es un subconjunto de B. |
| A ⊂ B | A es un subconjunto propio de B. |
| A ⊈ B | A no es un subconjunto de B. |
| A ⊄ B | A no es un subconjunto propio de B. |
| A ∪ B | Unión de los conjuntos A y B. |
| A ∩ B | Intersección de los conjuntos A y B. |
| A - B | Diferencia entre los conjuntos A y B. |
| A Δ B | Diferencia simétrica entre los conjuntos A y B. |
| U | Conjunto universal |
| A' | Complemento del conjunto A. |
| Ø | Conjunto vacío. |
| P(A) | Conjunto de partes del conjunto A. |
| A x B | Producto cartesiano A por B. |
Simbología de la lógica de predicados para conjuntos
| Símbolo | Significado |
|---|---|
| | | tal que |
| : | verifica |
| ∀ | Cuantificador universal: "para todo" |
| ∃ | Cuantificador existencial: "existe" |
| ∃! | Cuantificador de existencia única: "existe solo un" |
| ∴ | Por lo tanto |
Conjuntos numéricos
| Símbolo | Conjunto |
|---|---|
| N | Números naturales |
| Z | Números enteros |
| Q | Números racionales |
| I | Números irracionales |
| R | Números reales |
| C | Números complejos |
Bibliografía
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
- Vidal, J. (2010). Teoría de conjuntos. Universidad de Valencia.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.
Otros artículos
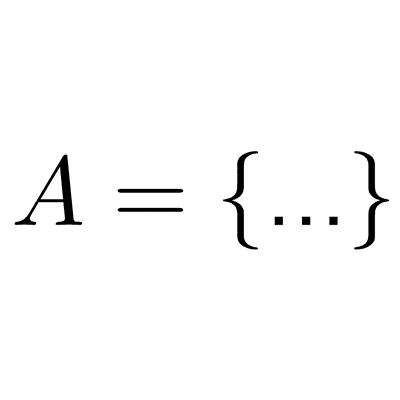
Qué es un conjunto en matemáticas
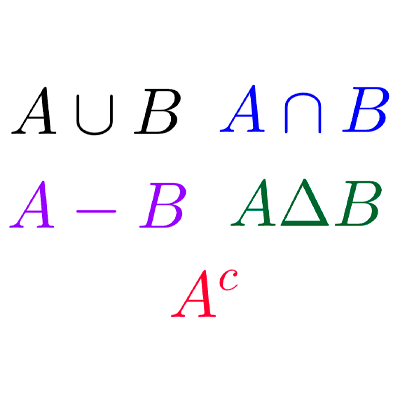
Operaciones entre conjuntos
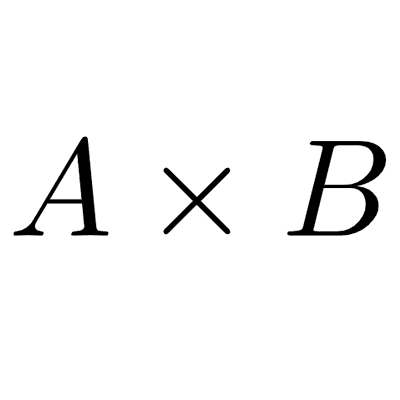
Producto cartesiano y pares ordenados
Intervalos de números reales
Relaciones binarias entre conjuntos
Conjunto de partes

Determinación de conjuntos por extensión y comprensión

Cardinalidad de conjuntos

Inclusión de conjuntos

Subconjunto de un conjunto

Igualdad de conjuntos

Tipos de conjuntos matemáticos
Conjunto vacío

Conjunto unitario
1 Comentarios
Deja una respuesta


Muy buen trabajo, gracias, estaba en las nubes con este tema.