
Cardinalidad de conjuntos
En este artículo explicamos qué es y cómo calcular el cardinal de un conjunto. Veremos ejemplos con conjuntos finitos e infinitos y propiedades especiales.
Índice
¿Qué es el cardinal de un conjunto?
El cardinal de un conjunto es el número de elementos diferentes que contiene ese conjunto. El cardinal de un conjunto A se representa por |A| o Card(A).
Por ejemplo, el conjunto A={a, b, c} tiene tres elementos, por lo cual su cardinal o tamaño es ese número: |A|=3. El conjunto B={1, 2, 1} tiene dos elementos diferentes, pues el "1" se escribió dos veces, por lo tanto |B|=2.
Si dos conjuntos tienen la misma cardinalidad, entonces se dice que son equipotentes. Por ejemplo, los conjuntos C={6, 9, 0} y D={p, q, r} tienen ambos tres elementos diferentes, por lo tanto, son equipotentes y podemos escribir |C|=|D|.
La cardinalidad de un conjunto puede ser finita o infinita. Para conjuntos finitos, como los casos anteriores, el cardinal es un número entero no negativo que representa la cantidad de elementos distintos. Para conjuntos infinitos, como los conjuntos numéricos, se adopta una simbología especial.
Cardinal de un conjunto finito
Para calcular la cardinalidad de un conjunto finito, simplemente hay que contar el número de elementos únicos que tiene.
Ejemplos
- A = {1, 2, 3, 4, 4, 5} tiene cinco elementos diferentes, porque el elemento "4" se repite dos veces, entonces se cuenta solo como una. Por lo tanto, el cardinal de A es 5: |A|=5
- B = {-1, 5, 3, 7} tiene cuatro elementos únicos, por lo tanto, su cardinal es ese número: |B|=4
- C={verde, azul, morado, azul} tiene tres elementos únicos ("azul" se repite dos veces y se cuenta solo una), por lo tanto, |C|=3.
- D = {3, a, e, i, o, u, 3, o, 3} tiene seis elementos diferentes, pues "3" y "o" se repiten más de una vez y solo se cuenta una. Entonces, el cardinal es seis: |D|=6
Si el conjunto está dado por comprensión, primero hay que escribirlo por extensión (si es posible) para contar sus elementos y así determinar su cardinal.
Ejemplos
- J = {x | x es letra de la palabra “jueves”} está determinado por comprensión, escrito por extensión es J = {j, u, e, v, e, s}, el cual tiene cinco elementos diferentes, porque una de las letras se repite dos veces, entonces: |J|=5.
- El conjunto E = {x | x+1=3} está dado por comprensión. Su equivalente por extensión es E={2}, el cual tiene un solo elemento, entonces, su cardinal es uno: |E|=1. Los conjuntos cuyos cardinales son iguales a 1 se llaman unitarios, en este ejemplo, E es unitario.
Ejercicio: determine el cardinal de los siguientes conjuntos.
A = {x | x es alguna vocal}
B = {x | x es natural, par y menor o igual a 12}
C = {x | x-1=0}
D= {x, y, z, w, y}
Soluciones:
|A|=5
|B|=6
|C|=1
|D|=4
Propiedades
El cardinal de un conjunto finito cumple algunas propiedades que pueden ser de utilidad para calcularlo.
1) Cardinal del vacío
El cardinal del conjunto vacío es cero, es decir, |Ø|=0. Esto es evidente porque el conjunto vacío no tiene ningún elemento.
2) Cardinal de un subconjunto
Si un conjunto A es un subconjunto de otro conjunto B, entonces la cardinalidad de A es menor o igual que la cardinalidad de B. Simbólicamente, si A ⊆ B, entonces |A| ≤ |B|.
Si A es un subconjunto propio de B, entonces el cardinal de A es estrictamente menor que el cardinal de B. En símbolos, si A ⊂ B, entonces |A| < |B|.
3) Cardinal de la unión
El cardinal de una unión de dos conjuntos es la suma de los cardinales individuales menos el cardinal de la intersección de los conjuntos. En símbolos:
|A ∪ B| = |A| + |B| - |A ∩ B|
Si los conjuntos A y B son disjuntos (no tienen elementos en común), entonces la cardinalidad de su unión es simplemente la suma de sus cardinalidades individuales, es decir,
|A ∪ B| = |A| + |B|
4) Cardinal de la intersección
El cardinal de la intersección de dos conjuntos es la suma de las cardinalidades individuales menos la cardinalidad de la unión de los conjuntos. Es decir:
|A ∩ B| = |A| + |B| - |A ∪ B|
Si A y B son conjuntos disjuntos, entonces el cardinal de su intersección es cero.
5) Cardinal de la diferencia
La cardinalidad de la diferencia entre dos conjuntos A y B es igual a el cardinal de A menos la cardinalidad de la intersección de A y B, es decir:
|A - B| = |A| - |A ∩ B|.
6) Cardinal del complemento
El cardinal del complemento de un conjunto es igual al cardinal del universal menos el cardinal del conjunto, es decir,
|A’| = |U| - |A|
7) Cardinal de un producto cartesiano
La cardinalidad del producto cartesiano de dos conjuntos A y B es el producto de sus respectivas cardinalidades, es decir:
|A × B| = |A| ⋅ |B|
8) Cardinal de un conjunto de partes
La cardinalidad de un conjunto de partes, también llamado conjunto potencia, es igual a 2 elevado al número de elementos del conjunto. Si un conjunto tiene n elementos, entonces el cardinal de su conjunto de partes *2^n.*
Cardinal de un conjunto infinito
El cardinal de un conjunto infinito se expresa con símbolos especiales, ya que no pueden contarse la cantidad de elementos. Matemáticamente se dice que el cardinal de un conjunto infinito es un número transfinito.
Por ejemplo, el cardinal del conjunto de los números naturales se simboliza como ℵ₀ (aleph-cero o álef-cero). El cardinal del conjunto de los números reales se simboliza como c (continuo) o también ℵ₁ (aleph-uno o álef-uno).
Es intuitivo pensar que los conjuntos infinitos tienen la misma cantidad de elementos, porque son infinitos. Sin embargo, esto no es así, y puede demostrarse que hay conjuntos infinitos que son "más grandes" que otros conjuntos infinitos. En particular, el conjunto de los números reales tiene más elementos que el de los números naturales: *c>ℵ₀*
También puede demostrarse que conjuntos infinitos que parecen tener más elementos que otros, en realidad tienen la misma cantidad. Así, los cardinales del conjunto de los números enteros y de los números racionales son iguales al de los números naturales: |Q| = |Z| = |N| = ℵ₀. También, dos intervalos de números reales cualesquiera tienen la misma cantidad de elementos: c.
Bibliografía
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
- Vidal, J. (2010). Teoría de conjuntos. Universidad de Valencia.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.


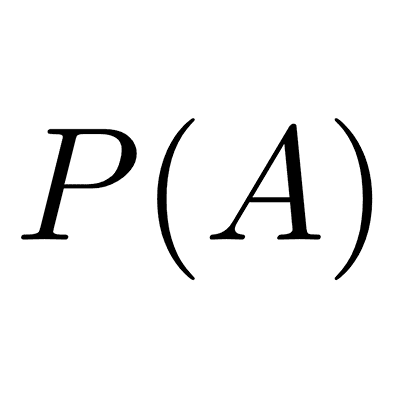
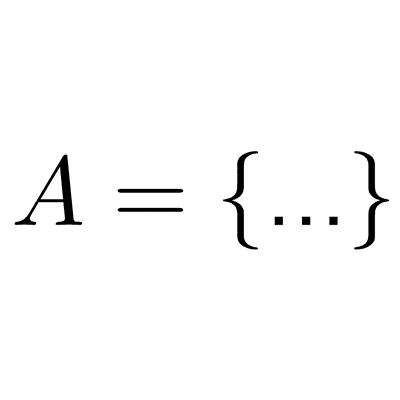
Deja una respuesta