Vértice de una función cuadrática
En este artículo explicamos qué es y cómo encontrar el vértice de una función cuadrática con ejemplos prácticos resueltos paso a paso.
Índice
¿Qué es el vértice?
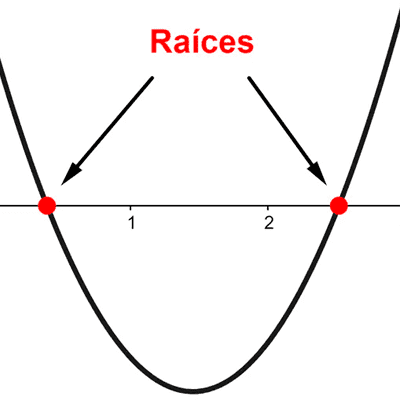
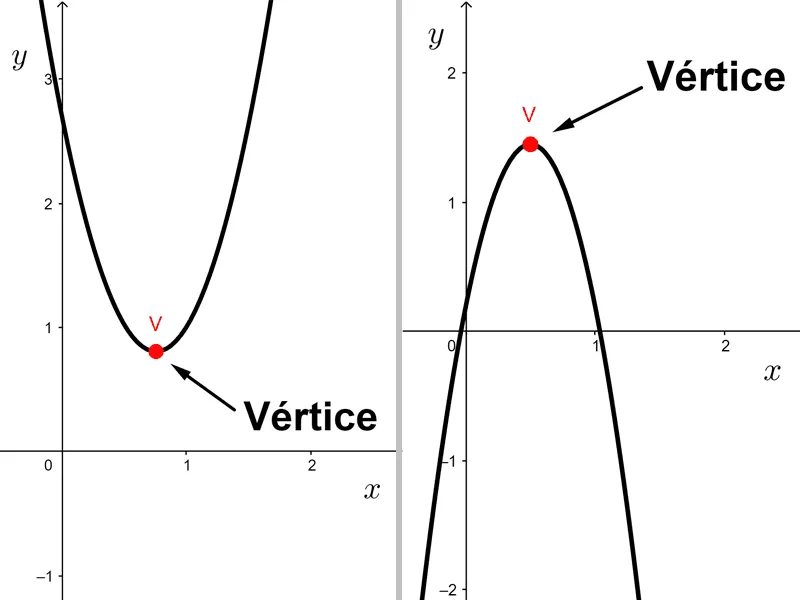
El vértice de una función cuadrática es el punto más bajo o más alto de su gráfica. Sabemos que la gráfica es una parábola. Si abre hacia arriba, tendrá un punto más bajo que todos; si abre hacia abajo, tendrá un punto más alto que todos.
El vértice también es también el punto de inflexión donde la función pasa de ser creciente a ser decreciente, o viceversa. A partir del vértice se puede determinar el eje de simetría de la función, que es la recta que divide la parábola en dos partes simétricas.
¿Cómo encontrar el vértice?
Las coordenadas del vértice pueden hallarse usando una fórmula muy sencilla que veremos a continuación, en la cual intervienen los coeficientes de la ecuación.
Fórmula para calcular el vértice
Sea f(x)=ax2+bx+c una función cuadrática. El vértice V de la función tiene coordenadas (h, k) donde:
*h=\dfrac{-b}{2a}*
*k=f(h)*
Si a>0, el vértice es un mínimo de la función. Si a<0, el vértice es un máximo.
Entonces, para obtener el vértice de una parábola, basta con tener la ecuación de la misma en forma polinómica (general), es decir, en la forma f(x)=ax2+bx+c. Las coordenadas de vértice se encuentran a partir de los coeficientes a y b.
- La coordenada x del vértice es: *h=\dfrac{-b}{2a}*
- La coordenada y del vértice es: *k=f(h)*
Entonces, para hallar la coordenada y del vértice, hay que evaluar la función en el punto h que se halló anteriormente.
Ejercicios resueltos
Ejercicio 1: Hallar el vértice de la función *f(x)=-2x^2+8x-5* y determinar si este es máximo o mínimo.
Solución:
Identificamos los coeficientes que necesitamos: *a=-2,b=8* y los reemplazamos en la fórmula del vértice:
*h=\dfrac{-b}{2a}=\dfrac{-8}{2\cdot(-2)}=\dfrac{-8}{-4}=2*
*k=f(h)=f(2)=-2(2)^2+8(2)-5=3*
Por tanto, el vértice de *f* es *V=(2,3).* Por ser *a* un número negativo, el vértice corresponde al máximo de la función.
Ejercicio 2: Determine el vértice de la función *f(x)=\dfrac{3}{4}x^2-2x+9*
Solución:
Identificamos los coeficientes que usaremos: *a=\dfrac{3}{4}, b=-2* y los sustituimos en la fórmula:
*h=\dfrac{-b}{2a}=\dfrac{-(-2)}{2\cdot\dfrac{3}{4}}=\dfrac{2}{\dfrac{3}{2}}=\dfrac{4}{3}*
*k=f(h)=f\left(\dfrac{4}{3}\right)=\dfrac{3}{4}\cdot\left(\dfrac{4}{3}\right)^2-2\cdot\left(\dfrac{4}{3}\right)+9=\dfrac{23}{3}*
El vértice es entonces *V=\left(\dfrac{4}{3},\dfrac{23}{3}\right).* Por ser *a* un número positivo, el vértice corresponde a un mínimo de la función.
Ejercicio 3: Calcular el vértice de la función *f(x)=x^2+3* y determinar si es mínimo o máximo.
Solución:
En este caso tenemos una función cuadrática incompleta, pues uno de los coeficientes vale cero. Extraemos los que utilizaremos: *a=1, b=0* y sacamos las coordenadas del vértice:
*h=\dfrac{-b}{2a}=\dfrac{-0}{2\cdot1}=0*
*k=f(h)=f(0)=(0)^2+3=3*
El vértice de es *V=(0,3)* y, por ser *a* positivo, corresponde al mínimo de *f.*
Ejercicio 4: Sacar el vértice de la función *f(x)=-6x^2*
Solución:
Otra vez tenemos una función cuadrática incompleta, pues dos coeficientes valen cero. Identificamos los que usaremos: *a=-6, b=0* y sustituimos en la fórmula:
*h=\dfrac{-b}{2a}=\dfrac{-0}{2(-6)}=0*
*k=f(h)=-6(0)^2=0*
Entonces, el vértice es *V=(0,0)* y corresponde a un máximo por ser *a* un número negativo.
Bibliografía
- Chorny, F., Casares, P. y Salpeter, C. (2015). Matemática 4. Editorial Estrada.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.



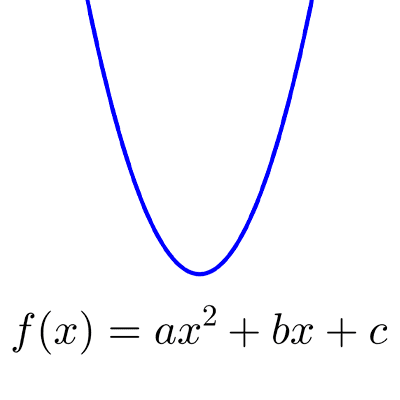


Deja una respuesta