Raíces de una función cuadrática
En este artículo explicamos qué son y cómo calcular las raíces de una función cuadrática utilizando tanto la fórmula general como otros métodos dependiendo del valor de los coeficientes de la función.
Índice
¿Qué son las raíces?
Las raíces o ceros de una función son los valores de x donde esta se anula, es decir, para los cuales f(x)=0. Geométricamente, las raíces son los puntos donde la gráfica de la función corta al eje x.
Sustituyendo f(x) por 0 en una función cuadrática se obtiene la ecuación ax² + bx + c = 0. Esta puede ser resuelta mediante la fórmula resolvente para ecuaciones cuadráticas, también llamada fórmula general o de Bhaskara:
*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*
Habiendo una raíz cuadrada en esta fórmula, sabemos que solo existe si su radicando es no negativo, siendo en caso contrario un número imaginario. Este radicando recibe el nombre de discriminante, y se lo denota con la letra griega delta mayúscula:
Δ = b²- 4ac
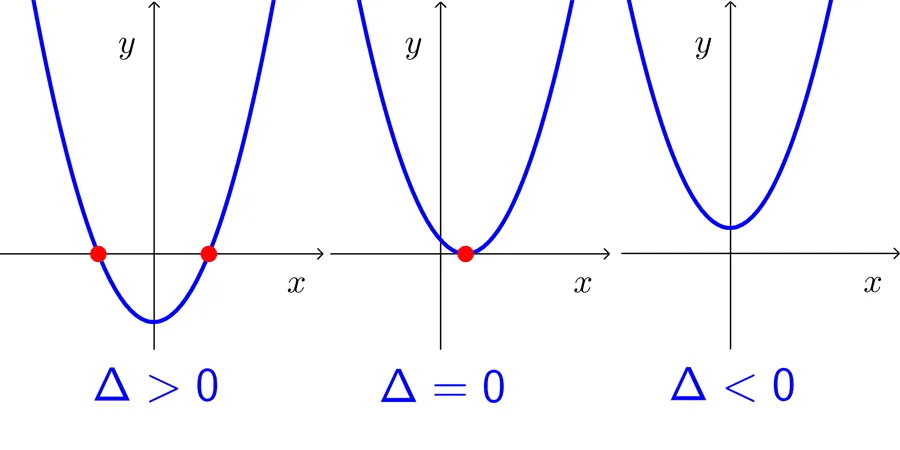
La importancia del discriminante radica en que nos dirá si la función cuadrática tiene o no raíces reales. Pueden darse tres casos:
- Si el discriminante es positivo, la función tiene dos raíces reales diferentes.
- Si el discriminante es cero, la función tiene una raíz real de multiplicidad 2.
- Si el discriminante es negativo, la función no tiene raíces reales.
En general, para hallar las raíces de una función cuadrática, debemos seguir los siguientes pasos:
- Igualar la expresión a cero.
- Identificar cada uno de los coeficientes: a, b y c.
- Reemplazar los coeficientes en la fórmula resolvente para hallar las raíces.
Sin embargo, existen circunstancias donde utilizar esta fórmula no es el camino más adecuado (aunque sigue siendo totalmente válida), veremos a continuación algunos casos que pueden darse cuando queremos hallar las raíces de una función cuadrática.
Encontrar los ceros de una función cuadrática resulta de utilidad para, por ejemplo, poder escribirla en forma factorizada y conocer los valores donde la gráfica corta al eje horizontal.
Primer caso: b=0
La función cuadrática no tiene coeficiente b y adquiere la forma f(x) = ax² + c. Para hallar los ceros debemos resolver la ecuación ax² + c = 0. No es necesaria la fórmula resolvente en este caso, pues podemos despejar x de forma fácil:
*ax^2=-c*
*x^2=-\dfrac{c}{a}*
*x=±\sqrt{-\dfrac{c}{a}}*
Sabemos que en los números reales no existen las raíces cuadradas de números negativos, por lo que la función tendrá raíces reales solo si ese radicando es no negativo. No es necesario memorizar la fórmula, con entender de donde proviene es suficiente para resolver los ejercicios.
Ejercicio 1: Hallar las raíces de la función *f(x)=x^2-1*
Solución:
1. Igualamos la ecuación a cero: *x^2-1=0*
2. Despejamos *x:*
*x^2=1*
*x=±\sqrt{1}*
El radicando es positivo, por tanto hay raíces reales. Ellas se obtienen con cada uno de los signos de la raíz cuadrada:
*x_1=\sqrt{1}=1*
*x_2=-\sqrt{1}=-1*
Ejercicio 2: Encontrar los ceros de la función *g(x)=3x^2-5*
Solución:
1. Igualamos a cero la ecuación: *3x^2-5=0*
2. Despejamos *x:*
*3x^2=5*
*x^2=\dfrac{5}{3}*
*x=±\sqrt{\dfrac{5}{3}}*
El radicando es positivo, por tanto hay ceros reales. Los hallamos usando cada signo de la raíz:
*x_1=\sqrt{\dfrac{5}{3}}≈1,29*
*x_2=-\sqrt{\dfrac{5}{3}}≈-1,29*
Ejercicio 3: Determinar las raíces de la función *h(x)=4x^2+3*
Solución:
1. Igualamos la ecuación a cero: *4x^2+3=0*
2. Despejamos *x:*
*4x^2=-3*
*x^2=-\dfrac{3}{4}*
*x=±\sqrt{-\dfrac{3}{4}}*
Por ser negativo el radicando, la función no tiene raíces reales, pues no podemos resolver dicha operación en este campo numérico.
Segundo caso: c=0
La función cuadrática no tiene término independiente c y toma la forma f(x)=ax²+bx. Para calcular las raíces debemos resolver la ecuación ax²+bx=0. La fórmula general puede aplicarse, pero tampoco es necesaria en este caso, pues podemos sacar como factor común a x:
*x(ax+b)=0*
Por propiedad de los números reales, un producto es nulo cuando alguno de sus factores es nulo, o sea:
*x=0*
*ax+b=0→x=-\dfrac{b}{a}*
Entonces, las raíces de la función son *x_1=0* y *x_2=-\dfrac{b}{a}.*
No es necesario memorizar estas fórmulas, pues con saber la lógica del procedimiento es suficiente para resolver los problemas.
Pasos para hallar las raíces de una función cuadrática cuando c es cero:
- Igualar la ecuación a cero.
- Sacar factor común x.
- Hallar las dos soluciones de la ecuación usando la propiedad del producto nulo.
Ejercicio 1: Hallar las raíces de la función *f(x)=5x^2-2x*
Solución:
1. Igualamos la ecuación a cero: *5x^2-2x=0*
2. Sacamos factor común x: *x(5x-2)=0*
3. Hallamos las dos soluciones:
*x=0*
*5x-2=0→x=\dfrac{2}{5}*
Las raíces de la función son:
*x_1=0*
*x_2=\dfrac{2}{5}*
Ejercicio 2: Encontrar los ceros de la función *g(x)=-9x^2+\dfrac{5}{4}x*
Solución:
1. Igualamos a cero: *-9x^2+\dfrac{5}{4}x=0*
2. Sacamos a x como factor común: *x(-9x+\frac{5}{4})=0*
3. Despejamos las dos soluciones:
*x=0*
*-9x+\dfrac{5}{4}=0→x=\dfrac{5}{36}*
Los ceros de la función son:
*x_1=0*
*x_2=\dfrac{5}{36}*
Tercer caso: b≠0 y c≠0
La función cuadrática tiene todos sus coeficientes distintos de cero: f(x) = ax² + bx + c. En este caso, sí resulta conveniente utilizar la fórmula resolvente, pues al menos que nos encontremos con un trinomio cuadrado perfecto que podamos factorizar, no disponemos de otro método para encontrar las raíces.
Ejercicio 1: Calcular las raíces de la función *f(x)=-2x^2+8x-5*
Solución:
Debemos resolver la ecuación *-2x^2+8x-5=0*
Usamos la fórmula resolvente identificando primero cada coeficiente: *a=-2, b=8, c=-5*
*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*
*x=\dfrac{-8±\sqrt{8^2-4\cdot(-2)\cdot(-5)}}{2\cdot(-2)}*
*x=\dfrac{-8±\sqrt{24}}{-4}*
El discriminante *Δ=24* es positivo, por tanto la función tiene dos raíces reales diferentes. Las hallamos usando cada signo de la raíz cuadrada:
*x_1=\dfrac{-8+\sqrt{24}}{-4}≈0,78*
*x_2=\dfrac{-8-\sqrt{24}}{-4}≈3,22*
Ejercicio 2: Determinar los ceros de la función *g(x)=6x^2-24x+24*
Solución:
Hallamos las raíces resolviendo la ecuación *6x^2-24x+24=0* mediante la formula general con *a=6, b=-24, c=24:*
*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*
*x=\dfrac{24±\sqrt{(-24)^2-4\cdot6\cdot24}}{2\cdot6}*
*x=\dfrac{24±\sqrt{0}}{12}*
El discriminante *Δ* es cero, por tanto la función tiene una raíz real de multiplicidad 2:
*x=\dfrac{24}{12}=2*
Ejercicio 3: Hallar las raíces de la función *h(x)=x^2-6x+12*
Solución:
Buscamos las raíces resolviendo la ecuación *x^2-6x+12=0* con la formula ya conocida con *a=1, b=-6, c=12:*
*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*
*x=\dfrac{6±\sqrt{(-6)^2-4\cdot1\cdot12}}{2\cdot1}*
*x=\dfrac{6±\sqrt{-12}}{2}*
El discriminante es negativo, por lo cual la función *h* no tiene raíces reales.
