
Análisis de funciones cuadráticas
Un análisis de funciones cuadráticas implica estudiar y comprender las propiedades, comportamiento y características de las funciones de segundo grado. El análisis suele incluir los siguientes elementos:
- Gráfica: La gráfica de una función cuadrática es una parábola. El análisis de la gráfica permite obtener información sobre los puntos de corte de la parábola con los ejes, el vértice de la parábola, y la concavidad de la parábola.
- Vértice: El vértice de una función cuadrática es el punto más alto o más bajo de la parábola, según sea el caso.
- Eje de simetría: El eje de simetría de una función cuadrática es la línea que pasa por el vértice de la parábola y la divide en dos partes iguales.
- Dominio y rango: El dominio de una función cuadrática es el conjunto de todos los valores de x para los que la función está definida. El rango de una función cuadrática es el conjunto de todos los valores de f(x) para los que x está en el dominio de la función.
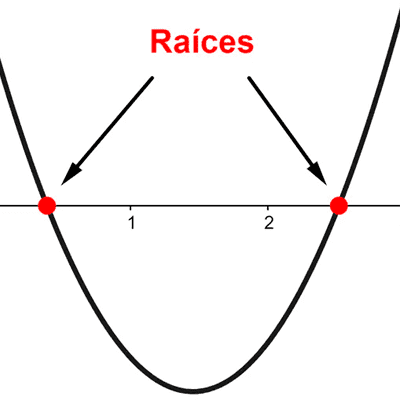
- Ceros o raíces: Los ceros o raíces de una función cuadrática son los valores de x que anulan a la función.
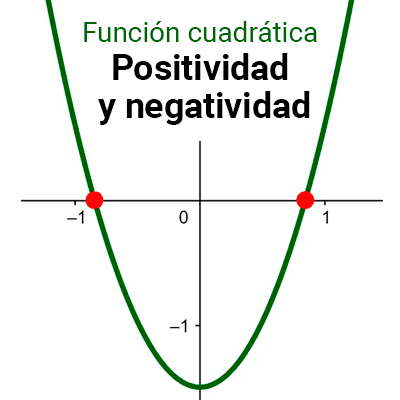
- Intervalos de positividad y negatividad: Los intervalos de positividad y negatividad de una función cuadrática son los intervalos de x para los que f(x) es positiva o negativa, respectivamente.
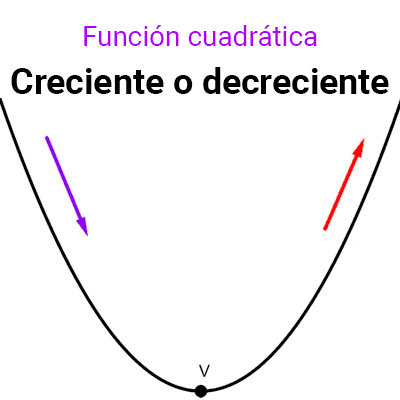
- Intervalos de crecimiento y decrecimiento: Los intervalos de crecimiento y decrecimiento de una función cuadrática son los intervalos de x para los que f(x) está creciendo o decreciendo, respectivamente.
A continuación podrás ver cómo encontrar cada uno de estos elementos paso a paso:



Deja una respuesta