
Cómo saber si el límite de una función existe
Para que exista el límite de una función en un punto debe ocurrir que los límites laterales sean iguales. Es decir que la función se acerca al mismo valor tanto si nos aproximamos al punto desde la izquierda o desde la derecha.
Simbólicamente: *\lim_{x\to a} f(x)=L~* si y solo si *~\lim_{x\to a^-} f(x)=L~* y *~\lim_{x\to a^+} f(x)=L*
Que los límites laterales existan en un punto y sean iguales significa que el límite existe. En cambio, el hecho de que los límites laterales sean distintos en un punto o no existan es suficiente para decir que no existe el límite de la función en el punto.
Es importante recordar que la función debe estar definida a ambos lados del punto para que exista el límite, aunque no es necesario que esté definida en el punto.
Ejemplos donde los límites existen
Veremos a continuación algunos ejemplos de funciones cuyos límites en el punto de interés existen.
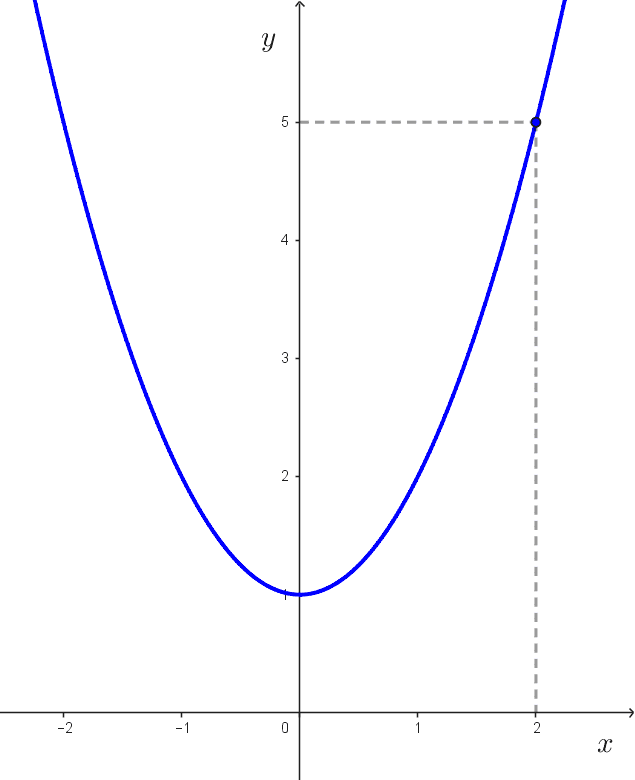
Ejemplo 1: Hallar *\lim_{x\to 2} (x^2+1)*
Mediante la gráfica o analíticamente podemos determinar que los límites laterales son iguales:
$$\lim_{x\to 2^-} (x^2+1)=5$$
$$\lim_{x\to 2^+} (x^2+1)=5$$
Por esta razón, concluimos que el límite existe y es igual a 5:
$$\lim_{x\to 2} (x^2+1)=5$$
Ejemplo 2: hallar *\lim_{x\to -2} f(x)* siendo:
$$f(x)=\begin{cases}-x+1~~\text{si}~~~x<-2 \\ 3~~\text{si}~~~x>-2\end{cases}$$
En este caso, la función está definida por partes y no tiene imagen en el punto de interés, pero como vimos en este artículo, la inexistencia de imagen no nos impide calcular el límite.
Comenzamos hallando los límites laterales, cuando x tiende a -2 por la izquierda, debemos usar la primera fórmula para las imágenes, y vemos que f(x) tiende a 3:
$$\lim_{x\to -2^-} f(x)=\lim_{x\to -2^-} (-x+1)=3$$
Si x se aproxima a -2 por la derecha, es necesario usar la segunda parte de la función, y las imágenes también se aproximan a 3. O sea:
$$\lim_{x\to -2^+} f(x)=\lim_{x\to -2^+} 3=3$$
Por la igualdad de los límites laterales, podemos concluir que el límite en -2 existe y es igual a 3.
$$\lim_{x\to -2} f(x)=3$$
Ejemplos donde los límites no existen
A continuación desarrollamos los casos posibles por los que una función no tiene límite en un punto.
Caso 1: Los límites laterales no coinciden.
Estudiemos si existe *\lim_{x\to 1} f(x)* siendo:
$$f(x)=\begin{cases}1~~~\text{si}~x<1 \\ x^2+1~~~\text{si}~x≥1\end{cases}$$
Nuevamente tenemos una función definida por partes. Si nos aproximamos a 1 por la izquierda, aplicará la primera parte de la función, resultando:
$$\lim_{x\to 1^-} f(x)=\lim_{x\to 1^-} 1=1$$
Si nos aproximamos a 1 por la derecha, debemos usar la segunda fórmula, o sea:
$$\lim_{x\to 1^+} f(x)=\lim_{x\to 1^+} (x^2+1)=2$$
Como puede verse, los límites laterales son distintos: *\lim_{x\to 1^-} f(x)≠\lim_{x\to 1^+} f(x).* Por tanto, *\lim_{x\to 1} f(x)* no existe. En la gráfica de la función se observa un salto en *x=1.*
Caso 2: La función crece o decrece sin cota.
Analicemos si existe *\lim_{x\to 0} \left(\dfrac{1}{x}\right)*
Utilizando una tabla o mirando la gráfica nos daremos cuenta de que cuando *x\to 0* por la izquierda, los valores de la función se hacen cada vez más grandes en valor absoluto hacia el lado negativo. De forma similar, cuando *x\to 0* por la derecha, los valores de la función se hacen cada vez más grandes hacia el lado positivo.
| x | -0,01 | -0,001 | -0,0001 | 0 | 0,0001 | 0,001 | 0,01 |
| f(x) | -100 | -1000 | -10000 | - | 10000 | 1000 | 100 |
En vista de esto, los límites laterales no existen, pues la función no se aproxima a ningún valor fijo, sino que decrece sin cota en el lado izquierdo y crece sin cota en el lado derecho. Como no existen los límites laterales, tampoco existe el límite en el punto. Por tanto:
*\lim_{x\to 0} \left(\dfrac{1}{x}\right)* no existe.
Nota: cuando los valores de la función se hacen cada vez más negativos cerca de un punto a, se simboliza como *\lim_{x\to a} f(x)=-\infty* y se lee “el límite cuando x tiende a a es menos infinito”. De forma análoga, cuando se hacen cada vez más grandes hacia el lado positivo, se escribe *\lim_{x\to a} f(x)=\infty* y se lee “el límite cuando x tiende a a es infinito”. Esto no quiere decir que los límites existan, sino que es una notación que indica el comportamiento de la función.
Caso 3: La función oscila entre dos valores.
Analicemos si existe *\lim_{x\to 0} \cos\left(\dfrac{1}{x}\right)*
Esta función tiene un comportamiento particular: podemos ver mediante su gráfica que las imágenes oscilan entre -1 y 1 cerca de cero. Como las imágenes no se acercan a un número real fijo, el límite de la función en el punto no existe. Evidentemente tampoco existen los límites laterales.
*\lim_{x\to 0} \cos\left(\dfrac{1}{x}\right)* no existe.
Comportamientos habituales asociados a la inexistencia del límite
- La función tiende a números diferentes según x tienda a un valor por derecha o por la izquierda.
- La función crece o decrece sin cota cuando x tiende a un valor.
- La función oscila entre dos números fijos cuando x tiende a un valor.
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.

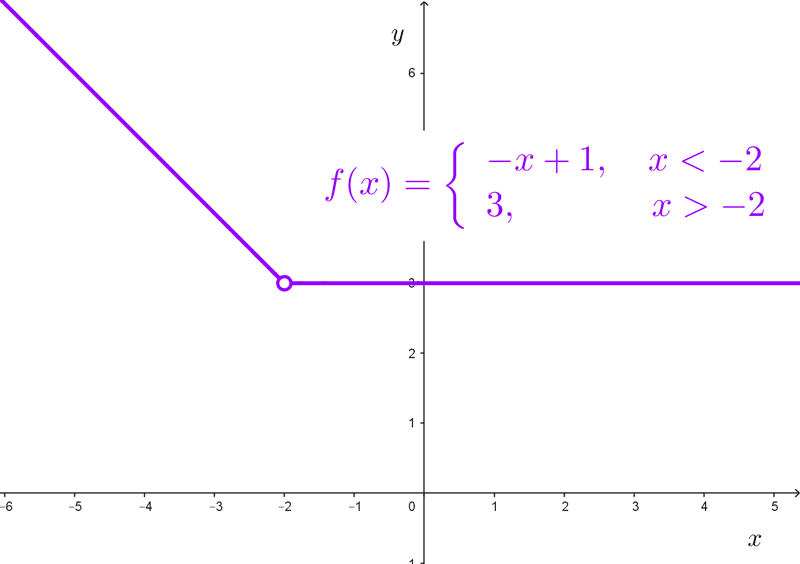
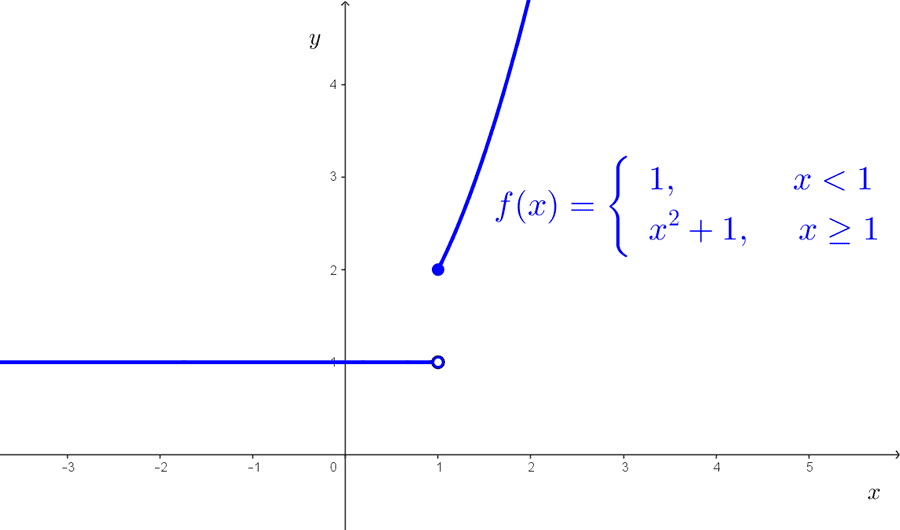




Deja una respuesta