Límites de funciones hiperbólicas
En este artículo estudiamos los límites de las funciones hiperbólicas en un punto especial y en el más infinito y menos infinito. Este trabajo nos permite conocer cuáles son las asíntotas horizontales o verticales de cada función, si es que existen.
Índice
Límites del seno hiperbólico
La función seno hiperbólico se define de la siguiente forma:
$$\sinh(x)=\dfrac{e^x-e^{-x}}{2}$$
Límite en cero:
$$\lim_{x\to 0}~\sinh(x)=0$$
Límites en el infinito:
$$\lim_{x\to \infty}~\sinh(x)=\infty$$
$$\lim_{x\to -\infty}~\sinh(x)=-\infty$$
Asíntotas: No tiene
Límites del coseno hiperbólico
La función coseno hiperbólico se define de la siguiente forma:
$$\cosh(x)=\dfrac{e^x+e^{-x}}{2}$$
Límite en cero:
$$\lim_{x\to 0}~\cosh(x)=1$$
Límites en el infinito:
$$\lim_{x\to \infty}~\cosh(x)=+\infty$$
$$\lim_{x\to -\infty}~\cosh(x)=+\infty$$
Asíntotas: No tiene
Límites de la tangente hiperbólica
La función tangente hiperbólica se define de la siguiente forma:
$$\tanh(x)=\dfrac{\sinh(x)}{\cosh(x)}=\dfrac{e^x-e^{-x}}{e^x+e^{-x}}$$
Límite en cero:
$$\lim_{x\to 0}~\tanh(x)=0$$
Límites en el infinito:
$$\lim_{x\to \infty}~\tanh(x)=1$$
$$\lim_{x\to -\infty}~\tanh(x)=-1$$
Asíntotas horizontales:
*y=1*
*y=-1*
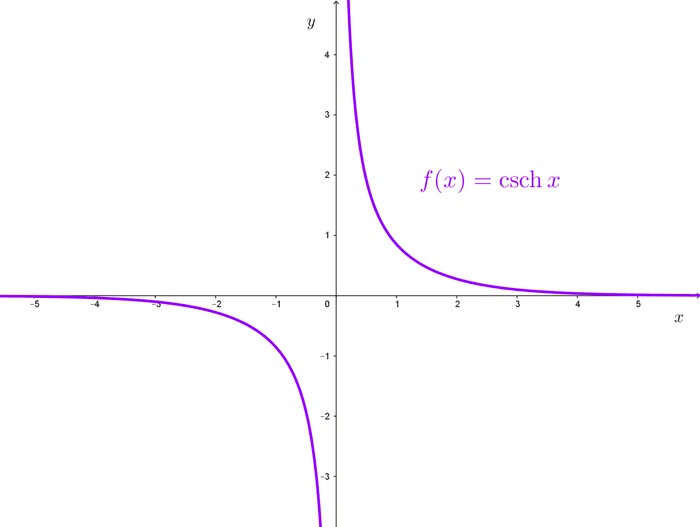
Límites de la cosecante hiperbólica
La función cosecante hiperbólica se define de la siguiente forma:
$$\text{csch}(x)=\dfrac{1}{\sinh(x)}=\dfrac{2}{e^x-e^{-x}}$$
Límite en cero:
$$\lim_{x\to 0}~\text{csch}(x)=\infty$$
Límites en el infinito:
$$\lim_{x\to \infty}~\text{csch}(x)=0$$
$$\lim_{x\to -\infty}~\text{csch}(x)=0$$
Asíntota horizontal: *y=0*
Asíntota vertical: *x=0*
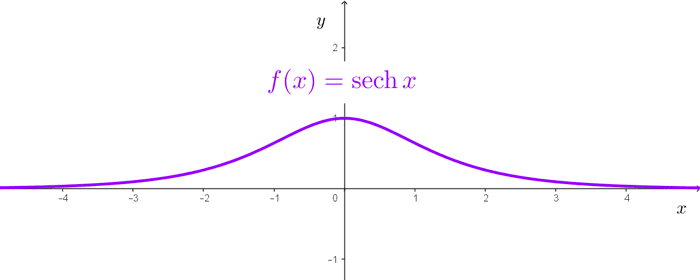
Límites de la secante hiperbólica
La función secante hiperbólica se define de la siguiente forma:
$$\text{sech}(x)=\dfrac{1}{\cosh(x)}=\dfrac{2}{e^x+e^{-x}}$$
Límite en cero:
$$\lim_{x\to 0}~\text{sech}(x)=1$$
Límites en el infinito:
$$\lim_{x\to \infty}~\text{sech}(x)=0$$
$$\lim_{x\to -\infty}~\text{sech}(x)=0$$
Asíntota horizontal: *y=0*
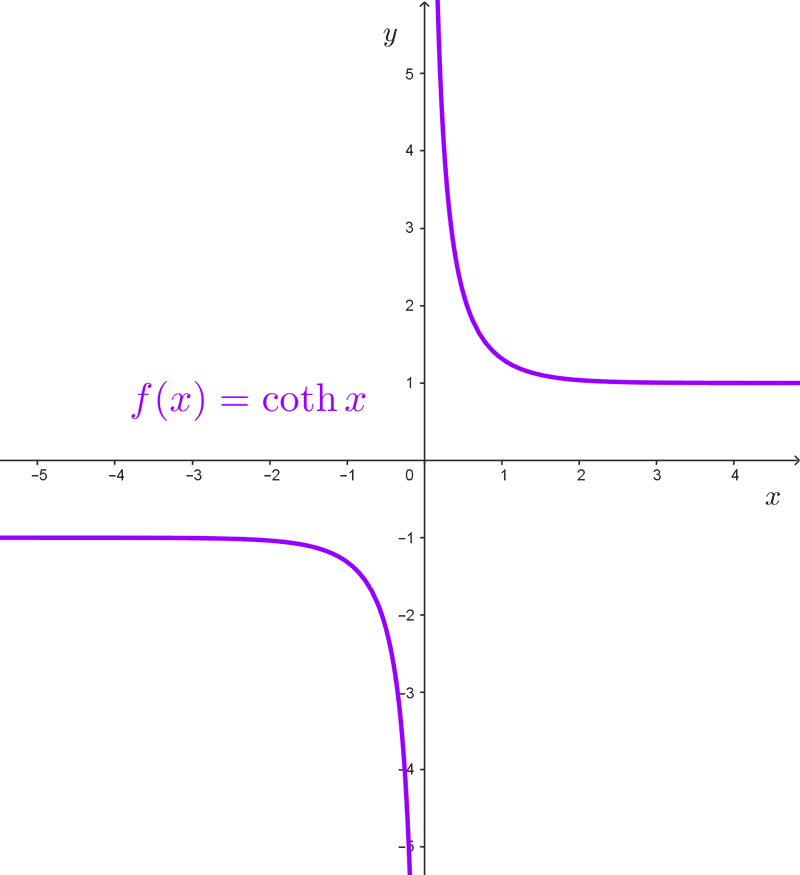
Límites de la cotangente hiperbólica
La función cotangente hiperbólica se define de la siguiente forma:
$$\coth(x)=\dfrac{1}{\tanh(x)}=\dfrac{e^x+e^{-x}}{e^x-e^{-x}}$$
Límite en cero:
$$\lim_{x\to 0}~\coth(x)=\infty$$
Límites en el infinito:
$$\lim_{x\to \infty}~\coth(x)=1$$
$$\lim_{x\to -\infty}~\coth(x)=-1$$
Asíntotas horizontales:
*y=1*
*y=-1*
Asíntota vertical: *x=0*
Subir
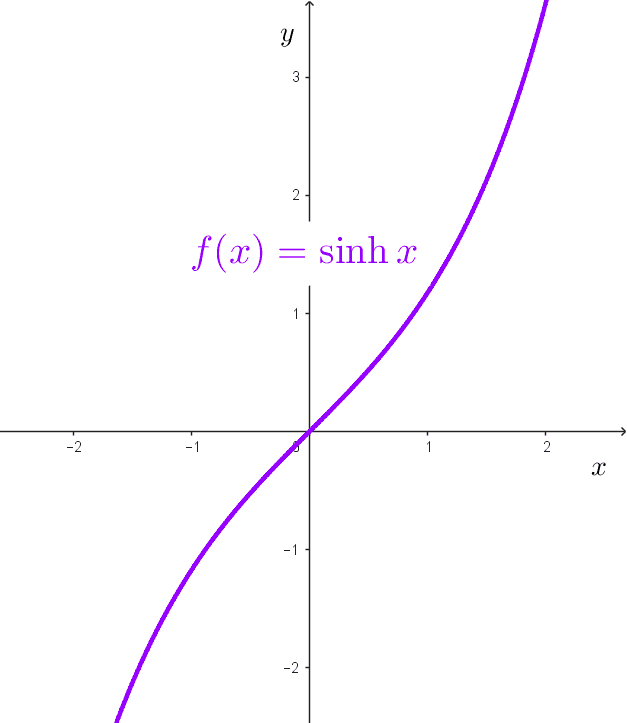
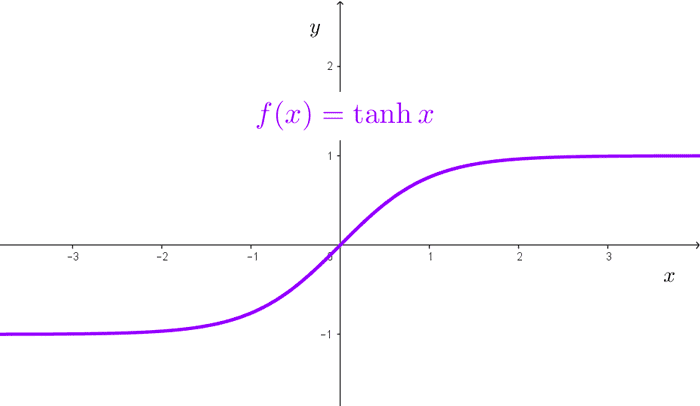
Deja una respuesta