
Quadratic function
In this article we explain what a quadratic function is and what are its elements and properties. In addition, we will see examples and the different ways in which its equation can be written.
Table of Contents
Definition
A quadratic function is a polynomial function of the second degree and has the following form:
*f(x)=ax^2+bx+c*
where *a,* *b,* and *c* are real numbers, and *a≠0.*
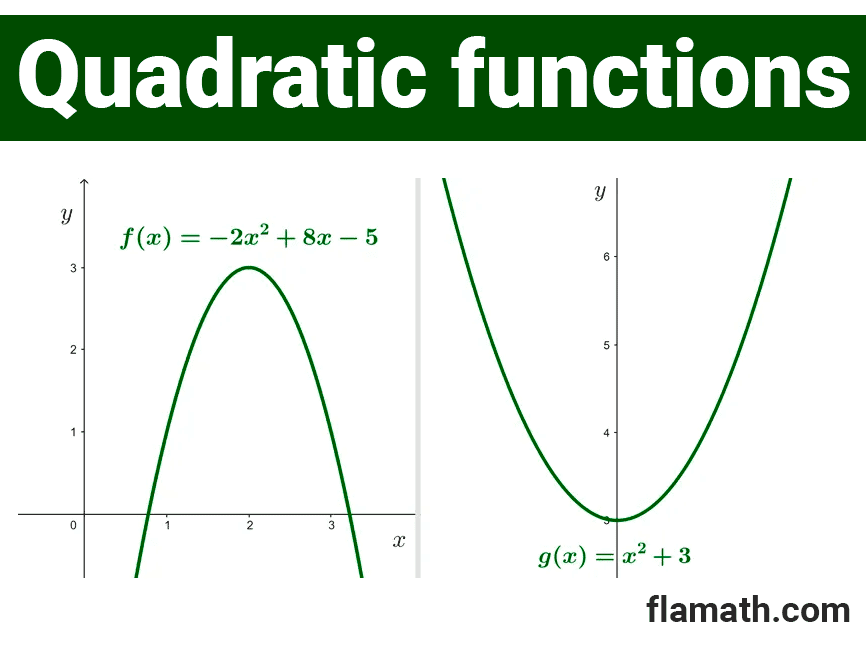
Some examples of quadratic functions are:
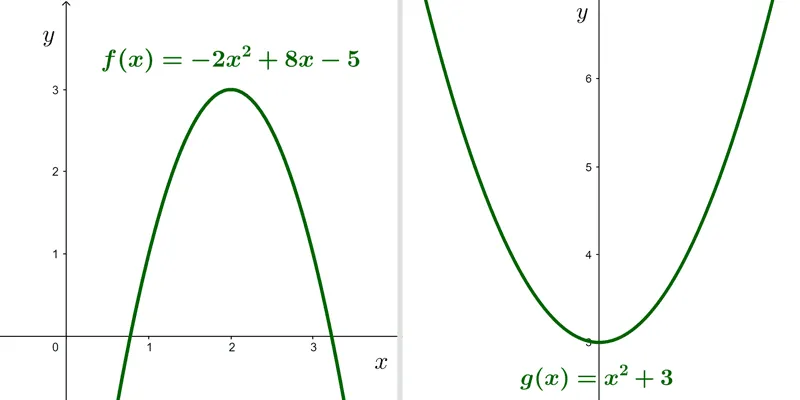
*f(x)=-2x^2+8x-5*
*g(x)=x^2+3*
*h(x)=6x^2*
*y=2x-x^2*
*v=-1+u^2+2u*
A function like *k(x)=2x-9,* is not quadratic because it lacks a quadratic term. Neither is *m(x)=x^3+3x^2-8x+5,* because although it contains a quadratic term, it is not a second-degree polynomial, but a third-degree one.
Elements and properties
Quadratic functions have a series of elements that determine their characteristics and allow us to study them; these elements are:
- Coefficients.
- Domain and Range.
- Graph.
- Vertex.
- Axis of Symmetry.
- Roots.
- Intersection with the y-axis.
We will now describe each of these components.
Coefficients
The coefficients of a quadratic function are the real numbers a, b, and c that appear in the general formula of the function, *f(x)=ax^2+bx+c.* Each of them has a special name:
- a is the coefficient of the quadratic term or leading coefficient. It can never be zero.
- b is the coefficient of the linear term. It can be zero.
- c is the constant term or independent term. It can be zero.
Similarly, the term *ax^2* is called the quadratic or leading term, the term *bx* is referred to as the linear term, and *c* is called the constant term.
Domain and Range
The domain of a function is the set of all values that the independent variable can take (usually denoted by x). The range of a function is the set of all values that the dependent variable can take (usually denoted as y or f(x)).
The domain of a quadratic function is always the set of real numbers, that is, *\mathbb{R}.* The range, on the other hand, depends on the coefficients as they will determine the values the function will take.
Graph
The graphical representation of a quadratic function is a curve called a parabola, which is symmetric with respect to a vertical line that we call the axis of symmetry.
When the parabola opens "upwards," the function is said to be convex. If the parabola opens "downwards," the function is concave. Whether it is one case or the other depends on the sign of the leading coefficient, which, if positive, will result in an upward-opening parabola; and if negative, it will create a downward-opening parabola.
Given a quadratic function *f(x)=ax^2+bx+c:*
The parabola opens upwards if *a>0*
The parabola opens downwards if *a<0*
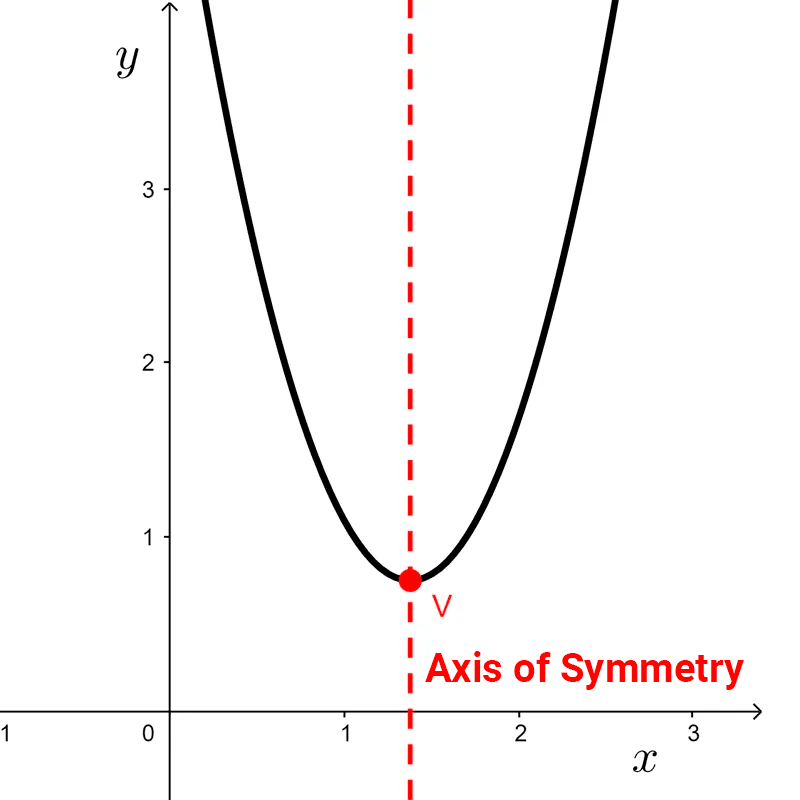
Vertex
If the parabola opens upwards, we can see that there is a point that is lower than all; if it opens downwards, there is a point that is higher than all. The lowest or highest point of the parabola is called the vertex. By definition, this point is minimum or maximum of the function, respectively.

The vertex V of the function *f(x)=ax^2+bx+c* has coordinates *(h,k)* where:
*h=\dfrac{-b}{2a}*
*k=f(h)*
If *a>0,* the vertex is a minimum of the function. If *a<0,* the vertex is a maximum.
Axis of Symmetry
We previously mentioned that the parabola is symmetrical with respect to a vertical line called the axis of symmetry (sometimes abbreviated as "axis"). Due to this symmetry, it is possible to find other points of the curve.
The axis of symmetry is the line parallel to the *y*-axis that passes through the vertex, and its equation is *x=\dfrac{-b}{2a}*
Zeros
The zeros, roots or x-intercepts of a function are the values of x where it cancels out, i.e., *f(x)=0.* At these points the graph of the function cuts the x-axis.
By substituting *f(x)* with *0* in a quadratic function, we obtain the equation *ax^2+bx+c=0.* This can be solved using the quadratic equation, also known as the general or Bhaskara's formula:
*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*
Since there is a square root in this formula, we know that it exists only if its radicand is non-negative; otherwise, it is an imaginary number. This radicand is called the discriminant, denoted by the uppercase Greek letter delta:
*Δ=b^2-4ac*
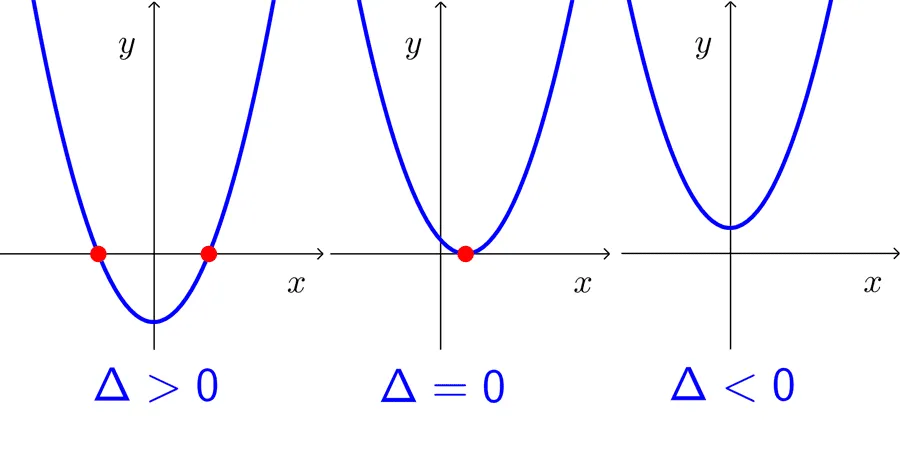
The importance of the discriminant lies in telling us whether the quadratic function has real roots or not. There can be three cases, which we will see below.
Let *f(x)=ax^2+bx+c* be a quadratic function, and *Δ=b^2-4ac* its discriminant:
- If the discriminant is positive, the function has two different real roots. In other words, the graph intersects the x-axis at two points.
- If the discriminant is zero, the function has one real root of multiplicity 2. In other words, the graph touches the x-axis at one point.
- If the discriminant is negative, the function has no real roots. In other words, the graph does not intersect or touch the x-axis.
Intersection with y-axis
The intersection of the graph of a function with the y-axis, if it exists, is unique and occurs when *x=0.* Since the domain of a quadratic function is *\mathbb{R},* zero is within the domain, and its image is:
*f(0)=a(0)^2+b(0)+c=c*
Therefore, the intersection of the graph of a quadratic function with the y-axis occurs at the point *(0,c).*
Equations of a quadratic function
There are three ways of expressing a quadratic function that have different utilities depending on what we are using them for.
General form
This is the form we have been working with so far and corresponds to a second degree polynomial:
*f(x)=ax^2+bx+c*
Factored form
A quadratic function can be expressed in factored form using its roots as follows:
*f(x)=a(x-x_1)(x-x_2)*
where *a* is the leading coefficient and *x_1,x_2* are the roots of *f.* If the discriminant is zero, it will happen that *x_1=x_2,* and the equation takes the form:
*f(x)=a(x-x_1)^2*
It is to be expected that if a quadratic function has no real roots, then it cannot be written in factored form. The factored form is also called the intercept form.
Vertex form
If the vertex of a quadratic function has coordinates *(h,k)*, we can write the equation as:
*f(x)=a(x-h)^2+k*
This is sometimes called the "standard form", although the general form is often called by the same name.
If we know the vertex, we can quickly arrive at this expression; if we don't know it, we can work with the general form in a process known as completing the square to reach the canonical form.
Applications of the quadratic function
Quadratic functions have many uses in various fields, such as science, business, engineering, and sports. These functions are useful, among other things, for modeling parabolic trajectories, predicting profits or losses in a business, determining maximum or minimum values, etc.
For example, for a quadratic function of income, it is possible to determine the maximum income; while for a quadratic function of cost, the minimum cost can be found. The process of searching for these ideal values is known as optimization.
Example: A shoe manufacturer can produce a certain shoe at a cost of $15 per unit. It is estimated that if the selling price of the shoe is $x, then the number of shoes sold weekly is *125-x.* Determine what should be the selling price for the manufacturer to achieve maximum weekly profit.
First, we need to determine the profit, which is defined as revenue minus production costs. In other words, profit is the gain.
We call *I(x)* the weekly income, which is nothing more than the product of the selling price of each shoe by the quantity of items sold:
*I(x)=x(125-x)*
Let *C(x)* be the total cost of the shoes sold each week. Since the total cost is the product of the cost of each item by the number of items sold,
*C(x)=15(125-x)*
If *U(x)* is the weekly profit, then:
*U(x)=I(x)-C(x)*
*U(x)=x(125-x)-15(125-x)*
*U(x)=(125-x)(x-15)*
*U(x)=-x^2+140x-1875*
The function *U* is quadratic with *a=-1, b=140.* Since *a<0,* the parabola opens downward, and the vertex is a maximum value. This value occurs when:
*x=\dfrac{-b}{2a}*
*x=70*
Remember that *x* was the price of each shoe. Therefore, the manufacturer will achieve a maximum weekly profit when the selling price is $70.
FAQs
What is a quadratic function?
A quadratic function is a polynomial algebraic function of second degree and has the form f(x)=ax^2+bx+c where a, b and c are real numbers and the leading coefficient (a) cannot be zero.
What are the elements of a quadratic function?
The main elements of a quadratic function are: coefficients, domain, range, graph, vertex, axis of symmetry, roots and y-intercept.
What is the graph of a quadratic function called?
The graph of a quadratic function is called a parabola. This curve is symmetric about a vertical axis, can open up or down depending on the coefficients of the function, and has a maximum or minimum point called the vertex.
What is the difference between a quadratic function and a quadratic equation?
A quadratic function is a specific type of mathematical function that describes a relationship between two variables. In contrast, a quadratic equation is an equality involving algebraic expressions of second degree.






Other articles that may interest you