How to find Domain and Range of a quadratic function
In this article we explain how to find the domain and range of a quadratic function with the different particular cases that can occur until we reach the general case. Also, we will see exercises solved step by step.
Table of Contents
Quadratic function domain
The domain of a quadratic function is the set of real numbers. This is because it is a polynomial function, and therefore, it inherits its domain. So, the quadratic function *f(x)=ax^2+bx+c* has a domain of *D_f=\mathbb{R}.*
Quadratic function range
The range depends on whether the parabola opens upward or downward and whether it is shifted upward, downward, left, or right. To calculate the range, we will look at the coefficients of the equation, namely, the numbers a, b, and c, called the leading coefficient, linear coefficient, and constant term, respectively. We will develop specific cases until we reach generalization.
First case: b=0 and c=0
If the linear term and the constant term are both zero, the function takes the form *f(x)=ax^2.*
The square of a number x will always result in a non-negative number, so our focus is on the sign of a, because if it is positive, the parabola will open upwards, causing the range to go from zero to positive infinity. If a is negative, the parabola will open downwards, resulting in the range going from negative infinity to zero. Notice in the graphs how this occurs.
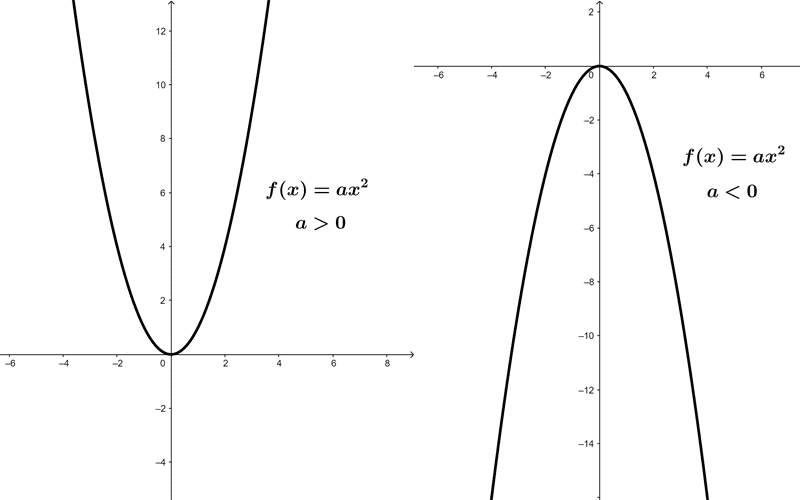
So, given a quadratic function that only has a quadratic term, the range will be an interval that has zero at one of its ends and depends on whether the leading coefficient is positive or negative.
Thus, given a function *f(x)=ax^2:*
If *a* is positive, *R_f=[0, +∞)*
If *a* is negative, *R_f=(-∞, 0]*
Examples:
- *f(x)=2x^2* *R_f=[0,+∞)*
- *g(x)=-5x^2* *R_g=(-∞, 0]*
Second case: b=0
If the linear coefficient is zero, the quadratic function takes the form *f(x)=ax^2+c.*
Introducing the term c does not pose much difficulty, as it will only shift the graph of *ax^2* upwards if c is positive or downwards if c is negative. With the help of a graph, we can deduce that what will actually affect it is the sign of a:

Given a quadratic function without a linear term, the range will be an interval that has the value of the constant term at one of its ends and depends on whether the leading coefficient is positive or negative.
Let the quadratic function be *f(x)=ax^2+c:*
If *a* is positive, *R_f=[c, +∞)*
If *a* is negative, *R_f=(-∞ , c]*
Examples:
- *f(x)=-x^2+3* has *R_f=(-∞, 3]* because *a=-1* is negative and *c=3*
- *g(x)=5x^2-2* has *R_g=[-2, +∞)* because *a=5* is positive and *c=-2*
Third case (general)
The function has the form *f(x)=ax^2+bx+c*
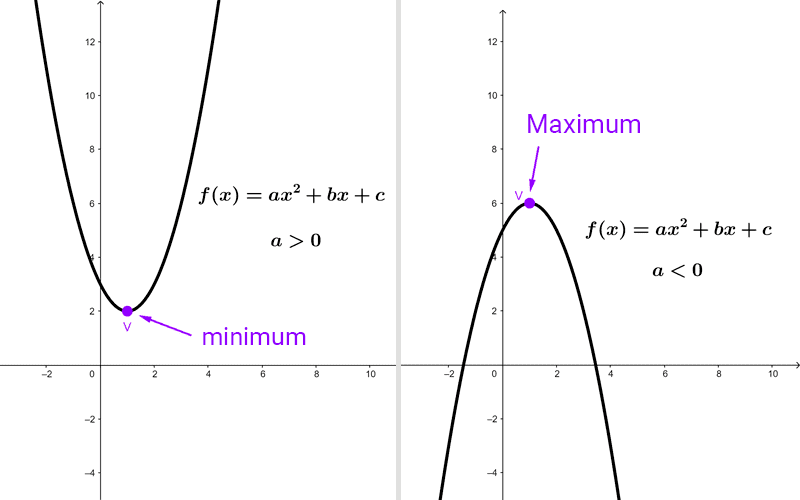
Introducing the term bx makes it challenging to predict at first glance how the graph of the function will move. However, knowing that the graph of a quadratic function is a parabola, we can calculate its vertex, which is an extreme point of the function.
Knowing this point will help us calculate the range because it will tell us exactly what the maximum or minimum value of the function is. If it is a maximum, then the range will go from negative infinity to it because there are no values greater than it. If it is a minimum, the range will go from it to positive infinity.
Whether the vertex is a maximum or minimum depends on the sign of a. If a is positive, the vertex will be a minimum. If a is negative, the vertex will be a maximum. See the following graph:
The vertex has coordinates *V=(h,k)* where:
*h=\dfrac{-b}{2a}*
*k=f(h)*
We are interested in the second coordinate, that is, *k=f(h),* as this will be the minimum or maximum of the function.
Given a general quadratic function, the range will be an interval that has the y-coordinate of the vertex (symbolized as k) at one of its ends and depends on whether the leading coefficient is positive or negative.
Let *f(x)=ax^2+bx+c*
If *a* is positive, *R_f=[k,+∞)*
If *a* is negative, *R_f=(-∞,k]*
where *k=f(h)* and *h=\dfrac{-b}{2a}*
Solved Exercises
Exercise 1: Calculate the domain and range of the function *f(x)=-2x^2+3x+1*
Solution:
We know that *D_f=\mathbb{R}*
Find the vertex to determine the range. *b* is the coefficient accompanying *x,* in this case, *b=3.* *a* is the coefficient accompanying *x^2,* in this case, *a=-2.*
The vertex is at the point *V=(h,k)* where:
*h=\dfrac{-b}{2a}*
*k=f(h)*
Substituting the values, we get:
*h=\dfrac{-3}{2(-2)}=\dfrac{3}{4}*
*k=f\left(\dfrac{3}{4}\right)=-2\left(\dfrac{3}{4}\right)^2+3\left(\dfrac{3}{4}\right)+1=\dfrac{17}{8}*
*V=\left(\dfrac{3}{4}; \dfrac{17}{8}\right)*
For the range, we are interested only in the second coordinate, *k=\dfrac{17}{8}*
Since *a=-2* is negative, the vertex is a maximum, and the range is:
*R_f=(-∞, \frac{17}{8}]*
Exercise 2: Find the range and domain of the function *f(x)=4x^2-x-3*
Solution:
*D_f=\mathbb{R}*
Identify *a=4,* *b=-1.* *V=(h, k)*
*h=\dfrac{-b}{2a}=\dfrac{-(-1)}{2(4)}=\dfrac{1}{8}*
*k=f\left(\dfrac{1}{8}\right)=4\left(\dfrac{1}{8}\right)^2-\dfrac{1}{8}-3=-\dfrac{49}{16}*
*V=\left(\dfrac{1}{8}; -\dfrac{49}{16}\right)*
Since *a=4* is positive, the vertex is a minimum, therefore:
*R_f=\left[-\dfrac{49}{16}; +∞\right)*
Exercise 3: Determine the domain and range of the function *f(x)=x^2+9*
Solution:
*D_f=\mathbb{R}*
We could calculate the vertex to find the range, but due to the absence of the term b, it is not necessary. We are facing the second case we saw before. Since *a=1* is positive and *c=9,* the range is:
*R_f=[9,+∞)*
Exercise 4: Find the domain and range of the function *f(x)=-x^2-14*
Solution:
*D_f=\mathbb{R}*
We are facing a function of the second case, as *a=-1* is negative and *c=-14,* the range is:
*R_f=(-∞,-14]*



Other articles that may interest you