How to find the zeros of a quadratic function

In this article we solve several problems on calculating zeros of quadratic functions using both the general formula and other methods depending on the value of the coefficients of the function.

Table of Contents

What are zeros?

The zeros or roots of a function are the values of *x* where it becomes zero, that is, *f(x)=0.* Geometrically, the zeros are the points where the graph of the function intersects the x-axis.

Geometric interpretation of roots of a quadratic function

Substituting *f(x)* with *0* in a quadratic function gives the equation *ax^2+bx+c=0.* This can be solved using the quadratic formula, also known as the general or Bhaskara's formula:

*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*

Since there is a square root in this formula, we know it exists only if its radicand is non-negative; otherwise, it becomes an imaginary number. This radicand is called the discriminant, denoted by the uppercase Greek letter delta:

*Δ=b^2-4ac*

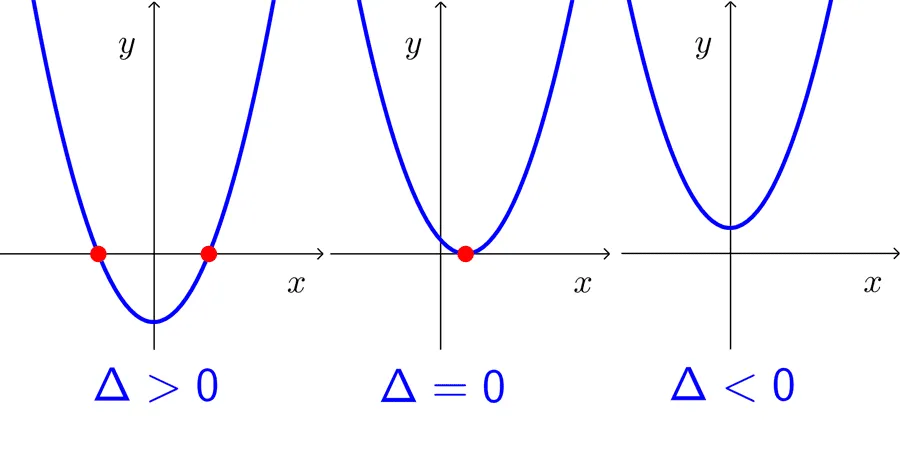
The significance of the discriminant lies in telling us whether the quadratic function has real zeros or not. Three cases can occur:

If the discriminant is positive, the function has two distinct real zeros.
If the discriminant is zero, the function has one real zero with multiplicity 2.
If the discriminant is negative, the function has no real zeros.

significance of the discriminant of a quadratic function

In general, to find the zeros of a quadratic function, we must follow these steps:

Set the expression equal to zero.
Identify each of the coefficients: a, b, and c.
Substitute the coefficients into the quadratic formula to find the zeros.

However, there are circumstances where using this formula may not be the most suitable approach (although it remains entirely valid). We will now explore some cases that may arise when we want to find the zeros of a quadratic function.

First case: b=0

The quadratic function has no coefficient *b* and takes the form *f(x)=ax^2+c*

To find the zeros, we need to solve the equation *ax^2+c=0*

The quadratic formula is not necessary in this case, as we can easily solve for *x:*

*ax^2=-c*

*x^2=-\dfrac{c}{a}*

*x=±\sqrt{-\dfrac{c}{a}}*

We know that in real numbers, there are no square roots of negative numbers. Therefore, the function will have real zeros only if this radicand is non-negative.

Memorizing the formula is not necessary, as understanding its derivation is sufficient to solve exercises.

Exercise 1: Find the zeros of the function *f(x)=x^2-1*

Solution:

1. Set the equation to zero: *x^2-1=0*

2. Solve for *x:*

*x^2=1*

*x=±\sqrt{1}*

The radicand is positive, so there are real zeros. They are obtained with each sign of the square root:

*x_1=\sqrt{1}=1*

*x_2=-\sqrt{1}=-1*

Exercise 2: Find the zeros of the function *g(x)=3x^2-5*

Solution:

1. Set the equation to zero: *3x^2-5=0*

2. Solve for *x:*

*3x^2=5*

*x^2=\dfrac{5}{3}*

*x=±\sqrt{\dfrac{5}{3}}*

The radicand is positive, so there are real zeros. We find them using each sign of the root:

*x_1=\sqrt{\dfrac{5}{3}}≈1.29*

*x_2=-\sqrt{\dfrac{5}{3}}≈-1.29*

Exercise 3: Determine the roots of the function *h(x)=4x^2+3*

Solution:

1. Set the equation to zero: *4x^2+3=0*

2. Solve for *x:*

*4x^2=-3*

*x^2=-\dfrac{3}{4}*

*x=±\sqrt{-\dfrac{3}{4}}*

As the radicand is negative, the function has no real zeros, as we cannot solve this operation in this numerical field.

Second case: c=0

The quadratic function has no constant term *c* and takes the form *f(x)=ax^2+bx*

To calculate the zeros, we need to solve the equation *ax^2+bx=0*

The general formula can be applied, but it is also not necessary in this case, as we can factor out *x:*

*x(ax+b)=0*

By the property of real numbers, a product is zero when any of its factors is zero, so:

*x=0*

*ax+b=0→x=-\dfrac{b}{a}*

Thus, the zeros of the function are *x_1=0* and *x_2=-\dfrac{b}{a}.*

Memorizing these formulas is not necessary, as understanding the logic of the procedure is sufficient to solve problems.

Steps to find the zeros of a quadratic function when c is zero:

Set the equation to zero.
Factor out x.
Find the two solutions of the equation using the property of the zero product.

Exercise 1: Find the zeros of the function *f(x)=5x^2-2x*

Solution:

1. Set the equation to zero: *5x^2-2x=0*

2. Factor out x: *x(5x-2)=0*

3. Find the two solutions:

*x=0*

*5x-2=0→x=\dfrac{2}{5}*

The zeros of the function are:

*x_1=0*

*x_2=\dfrac{2}{5}*

Exercise 2: Find the zeros of the function *g(x)=-9x^2+\dfrac{5}{4}x*

Solution:

1. Set the equation to zero: *-9x^2+\dfrac{5}{4}x=0*

2. Factor out x: *x(-9x+\frac{5}{4})=0*

3. Solve for the two solutions:

*x=0*

*-9x+\dfrac{5}{4}=0→x=\dfrac{5}{36}*

The zeros of the function are:

*x_1=0*

*x_2=\dfrac{5}{36}*

Third case: b≠0 and c≠0

The quadratic function has all coefficients different from zero: *f(x)=ax^2+bx+c*

In this case, it is convenient to use the resolvent formula, as unless we encounter a perfect square trinomial that we can factorize, we do not have another method to find the zeros.

Exercise 1: Calculate the zeros of the function *f(x)=-2x^2+8x-5*

Solution:

We need to solve the equation *-2x^2+8x-5=0*

Use the resolvent formula, identifying each coefficient first: *a=-2, b=8, c=-5*

*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*

*x=\dfrac{-8±\sqrt{8^2-4\cdot(-2)\cdot(-5)}}{2\cdot(-2)}*

*x=\dfrac{-8±\sqrt{24}}{-4}*

The discriminant *Δ=24* is positive, therefore the function has two different real zeros. Find them using each sign of the square root:

*x_1=\dfrac{-8+\sqrt{24}}{-4}≈0.78*

*x_2=\dfrac{-8-\sqrt{24}}{-4}≈3.22*

Exercise 2: Determine the zeros of the function *g(x)=6x^2-24x+24*

Solution: