Increasing and decreasing intervals of quadratic functions

The purpose of this article is to discuss the intervals in which a quadratic function increases or decreases and its relation to the vertex of the quadratic function. We begin with the necessary concepts and definitions and then move on to a series of exercises with detailed resolution.

Table of Contents

Increasing and decreasing Functions

A function is increasing on an interval of its domain when its values increase as x increases, and it is decreasing if its values decrease as x increases. We define these concepts precisely as follows.

A function *f* is called increasing on an interval *I* if

*f(x_1)<f(x_2)* whenever *x_1<x_2* in *I.*

It is called decreasing on *I* if

*f(x_1)>f(x_2)* whenever *x_1<x_2* in *I*

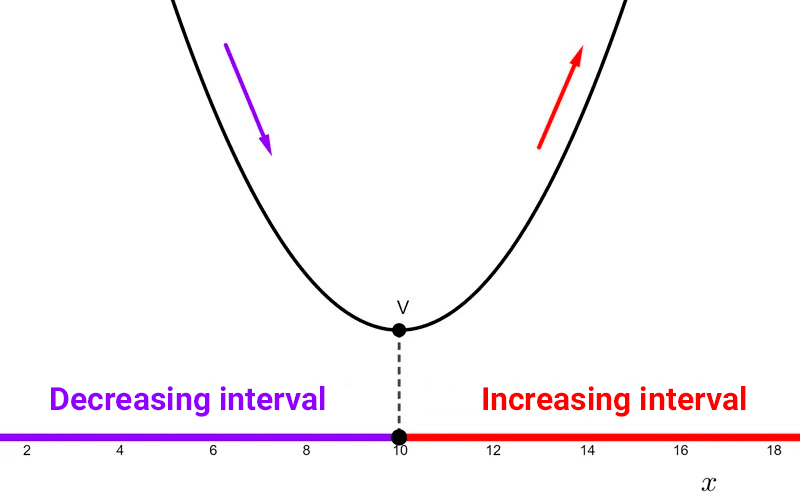
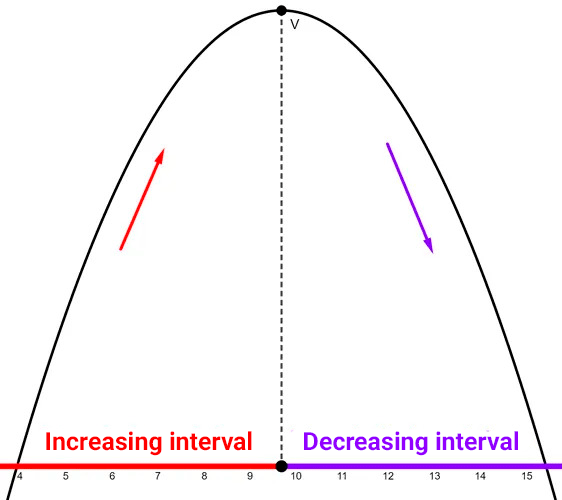
There are functions that can have intervals where they are increasing and others where they are decreasing. This is the case for quadratics, which have an increasing segment and a decreasing one. The transition from one segment to the other occurs at the vertex, also called the inflection point.

Let the quadratic function be *f(x)=ax^2+bx+c* with vertex *V=(h,k)*

If *a>0,* *f* is decreasing on *(-∞,h]* and increasing on *[h,+∞).*
If *a<0,* *f* is increasing on *(-∞,h]* and decreasing on *[h,+∞).*

Upward parabola with intervals of growth and decline — Upward parabola

Downward parabola with intervals of growth and decline — Downward parabola

Solved exercises

Exercise 1: Determine the intervals of growth, decline, and inflection point of *f(x)=-2x^2+8x-5*

Solution:

The parabola opens downward because *a<0,* so it starts with an increasing segment and follows with a decreasing one. Calculate the coordinates of the vertex *V=(2,3).* We are interested in the first component since the transition from increasing to decreasing occurs there.

Increasing interval: *(-∞,2]*

Decreasing interval: *[2,∞)*

The inflection point is the same as the vertex, i.e., *(2,3)*

Exercise 2: Calculate the increasing and decreasing intervals of the function *f(x)=6x^2-36x+54*

Solution:

The parabola opens upward because *a>0,* so there is a decreasing segment and then an increasing one. The vertex has coordinates *V=(3,0)*

Decreasing interval: *(-∞,3]*

Increasing interval: *[3,+∞)*

Exercise 3: Determine the increasing and decreasing intervals of the function *f(x)=x^2+2x*

Solution:

The parabola opens upward because *a>0.* Calculate the vertex and find that it has coordinates *V=(-1,-1)*

Decreasing interval: *(-∞,-1]*

Increasing interval: *[-1,+∞)*

Exercise 4: Calculate the increasing and decreasing intervals of the function *f(x)=-x^2+1*

Solution:

The parabola opens downward because *a<0.* The vertex has coordinates *V=(0,1)*

Increasing interval: *(-∞,0]*

Decreasing interval: *[0,+∞)*

Daniel Machado

Advanced student of Mathematics at Facultad de Ciencias Exactas, Químicas y Naturales. Universidad Nacional de Misiones, Argentina.