Números reales
En este artículo explicamos los números reales desde su concepto, definición, simbología, propiedades e interpretación gráfica. También trabajamos con el sistema de los números reales, el cual consiste en este conjunto numérico junto con las operaciones que pueden realizarse en él.
Índice
¿Qué es un número real?
Un número real es un tipo de número que corresponde a un punto en la recta numérica. Los números reales incluyen a los números racionales, que pueden escribirse como fracción, y también a los números irracionales, que no pueden expresarse como una fracción. Algunos ejemplos son: -2, 5, 3/2, π, √2, ∛7, 0, -5/4.
El conjunto de los números reales se simboliza con la letra R y es igual a la unión de los conjuntos de números racionales e irracionales:
*\mathbb{R}=\mathbb{Q}\cup\mathbb{I}*
Otra forma de expresar al conjunto de los números reales es usando el intervalo que va desde menos infinito hasta más infinito: *\mathbb{R}=(-\infty, +\infty)*
Los números reales se utilizan en diversas áreas de la ciencia y las matemáticas, especialmente en la expresión de cantidades continuas como la longitud y el tiempo. La capacidad de representar cantidades continuas con precisión hace que los números reales sean fundamentales en estas áreas.
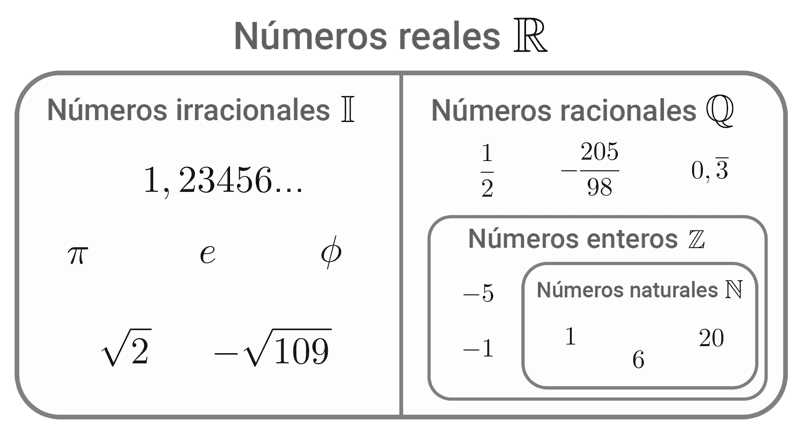
Todos los números naturales, enteros, racionales, irracionales y decimales son números reales. Esto se hace más evidente en el siguiente esquema, donde podemos observar todos los números que componen al conjunto de los reales.
Tenemos entonces dos tipos de números reales: los números racionales y los números irracionales. Además de lo visto en el gráfico, otros ejemplos de números reales son:
*-27;~~\sqrt[3]{8};* *~~-\dfrac{\sqrt{2}}{2};~~\dfrac{\pi}{9};* *~~\dfrac{e^7}{\sqrt{3}};~~3,17897546;* *~~2,645751311...*
Todo número real puede escribirse en forma decimal. Estas expresiones decimales pueden ser finitas o infinitas. En el caso de las expresiones decimales finitas, la parte decimal tiene un número limitado de dígitos después de la coma y eventualmente termina. Por ejemplo, el número 3,25 es una expresión decimal finita, ya que tiene solo dos dígitos después de la coma y luego se detiene.
Por otro lado, las expresiones decimales infinitas pueden ser periódicas o no periódicas.
- Las expresiones periódicas siguen un patrón repetitivo de dígitos después de la coma decimal. Por ejemplo, el número 1/3 tiene una expresión decimal infinita periódica: 0,333…, donde el "3" se repite infinitamente. El número 47/11 en forma decimal es 4,27272..., donde "27" se repite constantemente. Los tres puntos al final indican que hay más cifras pero no se escribieron.
- Las expresiones no periódicas no siguen un patrón repetitivo y los dígitos después de la coma decimal continúan infinitamente sin patrón. Por ejemplo, el número π (pi) tiene una expresión decimal infinita no periódica: 3,14159265358979…
Todas las expresiones decimales finitas e infinitas periódicas son números racionales, en cambio, las expresiones decimales infinitas no periódicas son números irracionales.
Descarga gratis la hoja de ejercicios de conjuntos numéricos. Haz clic en el botón de descargar.
Propiedades de los números reales
Las propiedades del conjunto de los números reales son:
- Es un conjunto infinito: los números reales forman un conjunto infinito, lo que significa que hay una cantidad ilimitada de números reales.
- No tiene primer ni último elemento: no existe un número real que sea más pequeño que todos ni uno que sea el más grande.
- Es un conjunto denso y completo: entre cualquier par de números reales distintos, hay infinitos números reales. La completitud implica que no hay "espacios vacíos" en la recta numérica real.
- Es un conjunto continuo: relacionado con lo anterior, la continuidad de los números reales se refiere a que no hay "saltos" en la recta numérica real; es decir, no hay huecos o brechas entre los números reales.
- Es un conjunto totalmente ordenado: los números reales pueden ser ordenados de acuerdo a su magnitud. Esto significa que, para cualquier par de números reales, uno es mayor que el otro, o son iguales.
La recta numérica real
El conjunto de números reales puede representarse mediante una recta, llamada recta real. Cada punto de esta recta representa un número real, y a cada número real le corresponde un único punto sobre la recta. Esto se llama correspondencia uno a uno (o biunívoca). Por esta razón, los números reales completan la recta numérica.
Sobre una recta, primero escogemos un punto arbitrario que llamaremos origen y lo asociamos con el número cero. Por convención, situamos los números reales positivos a la derecha del cero y los negativos a la izquierda. El cero no es positivo ni negativo. La flecha hacia la derecha indica que los números crecen en esa dirección.
Dados dos números reales distintos, será mayor aquel que más a la derecha se encuentre, del mismo modo, será menor aquel que más a la izquierda se encuentre. Por ejemplo, del gráfico extraemos que *\pi* es mayor a *\sqrt{2},* y al mismo tiempo *\pi* es menor que *23/5.*
Operaciones entre números reales
El conjunto de los números reales junto con las operaciones de suma (o adición) y multiplicación (o producto) se llama sistema de números reales. Las reglas del álgebra para este sistema nos permiten expresar hechos matemáticos en formas simples y concisas, y resolver ecuaciones para encontrar respuestas a preguntas matemáticas.
Expresamos a continuación las propiedades básicas del sistema de números reales con respecto a las operaciones de la suma y la multiplicación. Las letras a, b, c representan números reales.
1. Ley clausurativa, de cerramiento o cerradura
Cuando se realizan las operaciones de adición y multiplicación con números reales, los resultados son también números reales.
*a+b* es un número real
*ab* es un número real.
2. Ley asociativa
La suma de tres números reales puede obtenerse agrupando los sumandos en una de dos formas, y el producto de tres números reales puede determinarse agrupando los factores en una de dos maneras.
*a+(b+c)=(a+b)+c*
*a(bc)=(ab)c *
3. Ley conmutativa
La suma y el producto de dos números reales no son afectados por el orden de los números.
*a+b=b+a*
*ab=ba*
4. Ley distributiva
El producto es distributivo respecto a la suma de números reales.
*a(b+c)=ab+ac*
5. Existencia de elementos neutros (o de identidad)
Existen dos números reales distintos, *0* y *1,* llamados neutro aditivo y neutro multiplicativo, respectivamente, para los que tomando cualquier número real *a,* ocurre que:
*a+0=a*
*a\cdot1=a*
6. Existencia de inverso aditivo
Para cualquier número real *a,* existe un número real, llamado el inverso aditivo (o simétrico) de *a,* denotado por *-a,* para el que:
*a+(-a)=0*
Ejemplo: el inverso aditivo del número *5* es el número *-5*, pues si los sumamos da por resultado cero: *5+(-5)=0.* El inverso aditivo de *-20* es *20,* pues *-20+20=0.*
7. Existencia del inverso multiplicativo
Para cualquier número real *a,* excepto el *0,* existe un número real, llamado inverso multiplicativo o recíproco de *a,* denotado por *a^{-1},* tal que:
*a\cdot a^{-1}=1*
El inverso multiplicativo de *a* también puede escribirse como *\dfrac{1}{a}*
Ejemplo: el inverso multiplicativo del *2* es *\dfrac{1}{2},* pues multiplicando esos números da por resultado *1:*
*2\cdot \dfrac{1}{2}=1*
Para un número fraccionario *\dfrac{a}{b},* su inverso multiplicativo es *\dfrac{b}{a}* y se obtiene de permutar numerador y denominador.
Por ejemplo, el inverso de *\dfrac{4}{3}* es *\dfrac{3}{4}* pues:
*\dfrac{4}{3}\cdot \dfrac{3}{4}=1*
Es posible definir las operaciones de resta (o sustracción) y división (o cociente) en términos de la adición y la multiplicación, respectivamente.
Para los números reales *a* y *b,* la diferencia, *a-b* se define como:
*a-b=a+(-b)*
Si *b≠0,* entonces el cociente, *a:b,* se define como
*a:b=a\cdot \dfrac{1}{b}=\dfrac{a}{b}*
A continuación se presenta una lista de propiedades relacionadas con los números negativos:
- *-(-a)=a*
- *-(ab)=(-a)b=a(-b)*
- *-a=(-1)a*
- *(-a)(-b)=ab*
Muchas propiedades adicionales pueden derivarse de las propiedades básicas como en el caso de las siguientes propiedades:
Ley cancelativa
Si *a+c=b+c,* entonces *a=b*
Si *ac=bc* y *c≠0,* entonces *a=b*
*\dfrac{ac}{bc}=\dfrac{a}{b}* si *c≠0*
Ley de la multiplicación por cero
*a\cdot 0=0\cdot a=0*
Si *ab=0,* entonces *a=0* o *b=0* (o ambas).
A continuación vemos otras propiedades adicionales de números fraccionarios.
Fracciones equivalentes
*\dfrac{a}{b}=\dfrac{c}{d}* si y sólo si *ad=bc*
Adición y sustracción con común denominador
*\dfrac{a}{b}±\dfrac{c}{b}=\dfrac{a±c}{b}*
Adición y sustracción con distintos denominadores
*\dfrac{a}{b}±\dfrac{c}{d}=\dfrac{ad±bc}{bd}*
Multiplicación de fracciones
*\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{ac}{bd}*
División de fracciones
*\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a/b}{c/d}=\dfrac{a}{b}\cdot \dfrac{d}{c}=\dfrac{ad}{bc}*
División de cero y división por cero
*0:b=\dfrac{0}{b}=0,* *b≠0*
*0:0=\dfrac{0}{0}* es indefinido.
*a:0=\dfrac{a}{0}* es indefinido, *a≠0*
Signo de un número real
Podemos identificar dos grandes subconjuntos de los números reales, los cuales son los:
- Números reales positivos, denotado como *\mathbb{R}^{+}*
- Números reales negativos, denotado como *\mathbb{R}^{-}*
Nos referimos al signo de un número real como positivo si el número es positivo o negativo si el número es negativo. Dos números reales tienen el mismo signo si ambos son positivos o ambos son negativos. Dos números tienen signos contrarios o distintos si uno es positivo y el otro es negativo.
Se pueden probar los siguientes resultados acerca de los signos de productos y cocientes de dos números reales a y b, usando propiedades de negativos y cocientes.
Regla de los signos
Si *a* y *b* tienen el mismo signo, entonces *ab* y *\dfrac{a}{b}* son positivos.
Si *a* y *b* tienen signos contrarios, entonces *ab* y *\dfrac{a}{b}* son negativos.
Los recíprocos de estas proposiciones también son verdaderos.
Ejemplos:
Sean *a=7* y *b=-24.* Por tener diferente signo, el producto y el cociente de estos números será negativo:
*7\cdot (-24)=-168* es negativo.
*\dfrac{7}{-24}=-\dfrac{7}{24}* es negativo.
La misma prueba puede hacerse tomando números de igual signo.
Es importante reconocer la diferencia entre un número real negativo y el negativo de un número real. En particular, el negativo de un número real a puede ser positivo. Por ejemplo, si *a* es negativo, digamos *a=-5,* entonces el negativo *-a=-(-5)=5* es positivo. En general, tenemos las siguientes relaciones:
- Si *a* es positivo, entonces *-a* es negativo.
- Si *a* es negativo, entonces *-a* es positivo.
Relación de orden en los números reales
En la tabla siguiente definimos las nociones de mayor que y menor que para números reales *a* y *b.* Los símbolos *<* y *>* son signos de desigualdad y las expresiones *a>b* y *a<b* se llaman desigualdades.
| Notación | Definición | Terminología |
|---|---|---|
| *a>b* | *a-b* es positivo | *a* es mayor que *b* |
| *a<b* | *a-b* es negativo | *a* es menor que *b* |
Ejemplos:
- *5>3* porque *5-3=2* es positivo.
- *9<10* porque *9-10=-1* es negativo.
- *-4<-1* porque *-4-(-1)=-3* es negativo.
- *-6<1* porque *-6-1=-7* es negativo.
La ley que vemos a continuación nos permite comparar dos números reales cualesquiera.
Ley de tricotomía
La ley de tricotomía dice que, dados dos números reales cualesquiera, puede ocurrir solo una de tres posibilidades: el primero es mayor al segundo, el primero es menor al segundo o ambos son iguales. Simbólicamente, si *a* y *b* son números reales, entonces exactamente una de las siguientes expresiones es verdadera:
*a>b*
*a<b*
*a=b*
Una expresión de la forma *a<b<c* se denomina desigualdad continua y significa que *a<b* y *b<c;* decimos "*b* está entre *a* y *c*". Del mismo modo, la expresión *c>b>a* significa que *c>b* y *b>a.*
La notación *a≥b* se lee "*a* es mayor o igual que *b*" y significa que *a>b* o que *a=b* (pero no ambos). El símbolo *a≤b* se lee "*a* es menor o igual que *b*", significa que *a<b* o *a=b.* Expresiones de la forma *a≥b* y *a≤b* se denominan desigualdades no estrictas, porque *a* puede ser igual a *b.*
Limitaciones de los números reales
Los números reales son un conjunto fundamental en matemáticas, pero tienen limitaciones. La principal es que no existe solución real para la raíz cuadrada de un número negativo. Esta limitación se extiende a todas las raíces de índice par de números negativos. Por ejemplo, *\sqrt{-1}* no es un número real, pues ningún número real elevado al cuadrado da como resultado un número negativo. Una ecuación como *x^2+2=0* tampoco tiene solución en este conjunto numérico, pues despejando se llega a la expresión *x=\sqrt{-2}.*
Para superar esta limitación, se introduce el concepto de números complejos, los cuales son una extensión del conjunto de los números reales y se definen como números que incluyen tanto una parte real como una parte imaginaria. Con ellos será posible encontrar la raíz cuadrada (o cualquier índice par) de números negativos.
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 4. Puerto de Palos.
- Adunka, C., Mattiello, G., Moreno, A. y Repetto, A. (2005). Matemática II: EGB3. Universidad Nacional de Cuyo.
- Adunka, C., Mattiello, G., Moreno, A. y Repetto, A. (2006). Matemática I: Polimodal. Universidad Nacional de Cuyo.
- Becerril, M., García, P., Grimaldi, V. y Ponce, H. (2017). Matemática en secundaria. Santillana.
- Chorny, F., Casares, P. y Salpeter, C. (2015). Matemática 4. Editorial Estrada.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Leithold, L. (1994). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Matemática 3 ESO. (2011). Santillana Educación.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.




Deja una respuesta