Cómo graficar funciones
En este artículo veremos qué es la gráfica de una función, cómo realizarla y algunas herramientas que pueden ayudarlos en este proceso.
Índice
Gráfica de una función
Las funciones de variable real pueden ser representadas de manera visual mediante un plano donde se ha introducido un sistema de coordenadas cartesianas. Este sistema consiste en dos rectas llamadas ejes cartesianos, una vertical (llamada eje y o eje de ordenadas) y otra horizontal (llamada eje x o eje de abscisas). El punto donde se cortan es el origen de coordenadas denotado con la letra O. Ambas son rectas reales, es decir que cada punto de ellas representa a un número real.
Recordando que una función es un conjunto de pares ordenados, podemos interpretar a esos pares como puntos del plano y, representándolos en el sistema antes creado, tener acceso a una forma visual de las funciones. Esto es precisamente lo que se conoce como gráfica de la función (también llamado grafo).
Definición: Si f es una función con dominio D, la gráfica de f es el conjunto de puntos del plano cartesiano donde la primera coordenada es un elemento del dominio y la segunda es la imagen del mismo:
*\{(x,y)~|~x∈D∧y=f(x)\}*
En el plano cartesiano es habitual representar al dominio en el eje horizontal y al codominio y rango en el eje vertical. Para graficar una función podemos primero crear una tabla que nos dará algunos puntos, luego ubicarlos en el plano cartesiano y al final unir esos puntos fijándonos si tiene sentido hacerlo.
Ejemplo 1: gráfica de una función lineal
Sea la función *f(x)=x+1,* su gráfica es el conjunto de puntos *(x,y)* para los cuales *y=x+1.* Vemos que f es una función lineal y su dominio es el conjunto de los números reales. Recurrimos a una tabla donde encontramos las imágenes para algunos elementos del dominio (sería imposible hacerlo con todos, porque se trata de un conjunto infinito), luego formamos los puntos que ubicaremos en el plano cartesiano.
| x | y | (x, y) |
|---|---|---|
| -2 | -2+1=-1 | (-2, -1) |
| -1 | -1+1=0 | (-1, 0) |
| 0 | 0+1=1 | (0, 1) |
| 1 | 1+1=2 | (1, 2) |
| 2 | 2+1=3 | (2, 3) |
Fijándonos en la última columna acomodamos los puntos en el plano y debería quedarnos de la siguiente manera:
Para finalizar unimos los puntos y escribimos la función que estamos representando, con ello la gráfica estará terminada. Nótese que los puntos están alineados, lo cual es de esperarse porque la gráfica de una función lineal es una recta.
Nota: antes de unir los puntos debemos preguntarnos si tiene sentido hacerlo. En este ejemplo lo hicimos porque el dominio es todo *\mathbb{R}* y no hay puntos aislados. Si no ocurriese así, debemos tener cuidado.
Ejemplo 2: gráfica de una función cuadrática
Sea *f(x)=x^2,* identificamos el tipo de función y vemos que es una cuadrática, su dominio es todo *\mathbb{R}.* Recurrimos a una tabla similar al caso anterior y lo representamos en el plano cartesiano:
| x | y | (x, y) |
|---|---|---|
| -2 | *(-2)^2=4* | (-2, 4) |
| -1 | *(-1)^2=1* | (-1, 1) |
| 0 | *(0)^2=0* | (0, 0) |
| 1 | *(1)^2=1* | (1, 1) |
| 2 | *(2)^2=4* | (2, 4) |
Vemos claramente que, a diferencia del caso anterior, los puntos no están alineados. Esto es porque la gráfica de una función cuadrática es una figura geométrica llamada parábola. La vemos completa aquí:
Ejemplo 3: gráfica de la función raíz cuadrada
Sea *f(x)=\sqrt{x}.* La función raíz cuadrada tiene de dominio a todos los reales no negativos, con lo cual del lado negativo del eje x no habrá imágenes. Armamos una tabla tomando valores convenientes: aquellos que arrojan de imagen un número entero (podríamos tomar cualquier valor, pero para propósitos prácticos lo hacemos así).
| x | y | (x, y) |
|---|---|---|
| 0 | *\sqrt{0}=0* | (0, 0) |
| 1 | *\sqrt{1}=1* | (1, 1) |
| 4 | *\sqrt{4}=2* | (4, 2) |
| 9 | *\sqrt{9}=3* | (9, 3) |
Si repetimos el proceso anterior, nuestra gráfica completa se vería así:
Cortes de una gráfica con los ejes cartesianos
Es de utilidad, al realizar la gráfica de una función, hallar los puntos de corte de esta con los ejes horizontal y vertical, si existen. En el primer ejemplo vimos que *f(x)=x+1* corta al eje y en el punto *(0,1)* y al eje x en el punto *(-1,0).* Las funciones *f(x)=x^2* y *f(x)=\sqrt{x}* cortan a ambos ejes en el mismo punto: el origen de coordenadas (0, 0).
Intersección con el eje y
La intersección de la gráfica de una función f con el eje y si existe, es única, y se da cuando *x=0,* o sea, el punto de corte es *(0, f(0)).* En el caso de una función lineal, a la segunda coordenada del punto se la llama ordenada al origen. La propiedad de unicidad se da por la definición de función, pues si existieran dos puntos de corte, estaríamos hablando de una relación donde a un mismo valor *(x=0)* le corresponde más de uno, por tanto no estamos tratando con una función.
Para calcular este punto de intersección debemos hacer a la variable independiente igual a cero y hallar su imagen.
Ejemplo: *f(x)=2x+3*
Hacemos *x=0→f(0)=2(0)+3=3*
Por tanto, el punto de corte con el eje y es *(0,3).* En este caso, por ser una función lineal, *y=3* es la ordenada al origen.
Intersección con el eje x
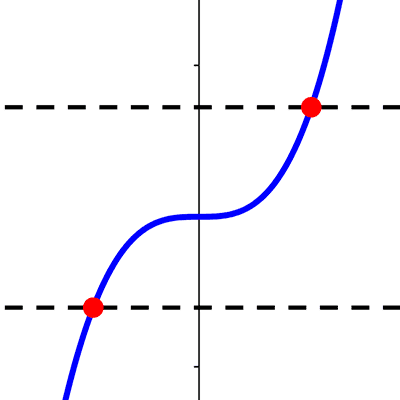
La intersección de la gráfica de una función f con el eje x se da cuando *f(x)=0,* al valor de x se lo llama cero o raíz de la función. A diferencia del caso anterior, pueden existir muchos puntos de corte con el eje x, todos ellos tendrán la forma (x, 0). En el esquema siguiente, *a_1* y *a_2* son ceros de la función f.
Para hallar estos puntos de intersección, igualamos la función a cero y despejamos x. Calcular estos puntos de corte en ocasiones no es tan rápido como en el caso anterior.
Ejemplo 1: *f(x)=2x+1*
Procedemos a igualando a cero: *2x+1=0*
Despejamos la x como es habitual *2x=-1→x=\dfrac{-1}{2}*
Entonces *x=-\frac{1}{2}* es un cero de la función. El punto de intersección es entonces *(-\frac{1}{2} , 0).*
Ejemplo 2: *f(x)= x^2-1*
Igualamos a cero: *x^2-1=0→x^2=1→x=1* o *x=-1*
Estos valores hallados son los ceros de la función. Los puntos de corte son *(-1,0)* y *(1,0)*
En el caso de tener funciones más complejas, el trabajo de encontrar ceros se dificulta y, en algunos casos, ante la falta de artificios algebraicos resulta imposible hallarlos. Mediante la gráfica de la función podemos estimar dónde se encontrarían, pero no calcularlos de manera exacta.
Programas para graficar funciones
Disponemos actualmente de muchos software que nos permiten graficar funciones introduciendo su fórmula. Entre ellas suelo utilizar y recomiendo a Geogebra (con el cual se realizaron los gráficos de las imágenes anteriores) y Desmos.
Geogebra
Este programa es gratuito y tiene una versión online, otra descargable para PC y una versión para dispositivos móviles. Basta con entrar a su página y dar en “iniciar calculadora”. Se desplegará un plano cartesiano donde podrán ser introducidas las reglas de definición de las funciones que queremos graficar. Podemos trabajar en dos dimensiones (como las funciones que tratamos en este artículo) y también trabajar en tres dimensiones.
Desmos
Igual que el caso anterior, este software es gratuito y funciona de manera online. Aunque no dispone de una versión descargable para PC, sí tiene una aplicación para móviles. Al ingresar a su página y pulsar en “calculadora gráfica” ya podemos introducir las funciones para que se grafiquen. Por el momento solo podemos hacer gráficos en dos dimensiones, suficiente cuando trabajamos con funciones de una variable.
