Funciones reales de variable real
En este artículo explicamos las funciones reales de variable real (o funciones real valuadas), es decir, aquellas donde las variables son números reales. Analizaremos su definición, dominio y rango, gráficas y veremos algunos ejemplos de las mismas.
Índice
¿Qué es una función real?
Recordemos que una función o aplicación es una regla que asigna a cada elemento de un conjunto, llamado dominio, un único elemento de otro conjunto, llamado codominio. Entonces, en las funciones reales lo que ocurrirá es que el dominio y el rango serán subconjuntos de números reales.
Sean A y B dos subconjuntos de números reales. Una función real de variable real o función escalar f es una regla que asigna a cada número real del conjunto A, un único número real del conjunto B.
El conjunto A se llama dominio de la función, el conjunto B se llama codominio. El recorrido o rango se define como el subconjunto de B formado por todas las imágenes de los elementos de A. Puede ocurrir que existan elementos del codominio que no están en el rango de la función.
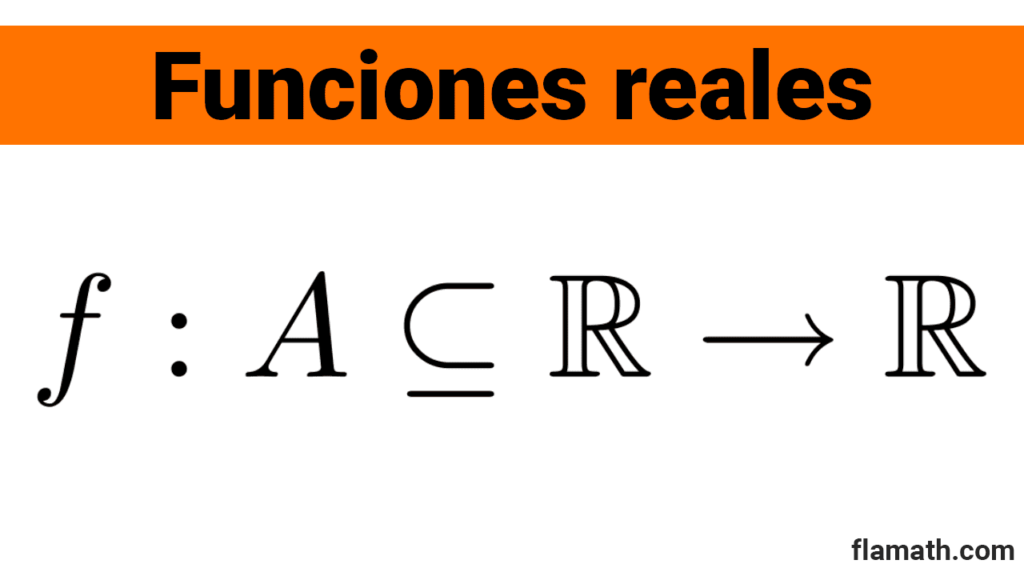
La simbología habitual utilizada en análisis matemático es $$f: A\subseteq \mathbb{R} \rightarrow \mathbb{R}$$ que se lee como "f es una función definida de reales en reales". También podríamos escribir $$f: A\rightarrow B, A\subseteq \mathbb{R}, B\subseteq \mathbb{R}$$ que se interpreta como "f es una función definida de A en B, A y B son subconjuntos de números reales".
Para la función escalar f, a cada elemento x del dominio A le corresponde un elemento y del rango. Este elemento y se llama valor de la función f en x, o imagen de x a través de f, y se denota como f(x), léase "f de x". Entonces, podemos decir que *y=f(x).* Como el valor de y depende de la elección de x, se la denomina variable dependiente; a x se la llama variable independiente. Entendido así, el dominio es el conjunto de todos los valores posibles de x y el rango es el conjunto de valores de y que corresponden a cada x.
Nota: al elemento x del dominio de la función se le suele llamar "argumento" o "preimagen" de la función.
La notación de funciones puede confundir al principio. Recordemos que f es el nombre de la función escalar, y f(x) es la imagen del elemento x del dominio de f. Entonces, resulta que f(x) es un elemento del rango de la función, por esa razón podemos escribir *y=f(x).*
Con frecuencia las funciones se definen mediante una fórmula o ecuación que nos da la relación que cumplen los elementos del dominio y el rango. Puede pasar que se utilice una única regla para calcular la imagen de cada uno de los elementos del dominio o bien que según sea el valor de la variable independiente se utilice una regla u otra para calcular su imagen (función definida por partes).
Por ejemplo: *y=6x^2+x+1 *
Utilizando la notación de funciones, podemos escribir esta ecuación como
*f(x)=6x^2+x+1*
Esta notación es útil porque nos informa de varias cosas:
- La variable independiente es x.
- La variable dependiente es f(x), que podemos escribir como y.
- El nombre de la función es f.
- Un elemento x del dominio tiene por imagen a *f(x)=6x^2+x+1.*
Si nos interesa, por ejemplo, conocer cuánto es el valor de la función cuando x=3, bastará preguntar “¿cuánto vale *f(3)*?”. El proceso de hallar el valor de y que corresponde a un x dado se conoce como evaluar la función.
El papel de la variable x en la ecuación puede entenderse como un hueco a llenar. Por ejemplo, la función *f(x)=6x^2+x+1* puede describirse como *f(~~~)=6(~~~)^2+(~~~)+1,* donde usamos paréntesis en lugar de x, y podría leerse como "f de algo es igual a seis veces ese algo al cuadrado, más el algo, más uno". Para evaluar *f(-2),* bastará con colocar *-2* en cada par de paréntesis:
*f(-2)=6(-2)^2+(-2)+1*
*=6\cdot 4-2+1*
*=23*
Nota: aunque es frecuente usar f como símbolo para denotar una función y x para la variable independiente, se pueden utilizar otros símbolos. Siempre que una función esté bien definida, no tienen mucha importancia los símbolos que se usen para escribirla. A modo de ejemplo, las siguientes ecuaciones definen todas la misma función:
*f(x)=x^2-4x+5*
*f(t)=t^2-4t+5*
*g(s)=s^2-4s+5*
Las letras utilizadas habitualmente para nombrar funciones son F, G, H, f, g, h, p, q, etc; para las variables suelen usarse r, s, t, u, v, w, x, y, z.
Dominio y rango
El dominio o campo de existencia de una función es el conjunto de todos los valores posibles que puede tomar la variable independiente. El conjunto imagen, rango o recorrido es el conjunto de todos los valores que puede tomar la variable dependiente. En las funciones reales, como es de esperarse, el dominio y el rango son subconjuntos de números reales.
Dominio: es el conjunto de números reales para los que la función está definida, o sea, que tienen imagen real a través de la función. Se lo denota como *D_f* o *Dom(f)*
*D_f=\{x\in \mathbb{R}~|~\exist~ f(x)\}*
El dominio de una función puede venir explícito con la misma; caso contrario, se tomará como dominio el conjunto más grande de números reales que arrojan como imagen un número real. En este último caso puede ser necesario hacer algunos cálculos usando la ecuación.
Ejemplos:
- La función *f(x)=\dfrac{1}{x^2-4},* *4≤x≤5* tiene un dominio definido explícitamente como *D_f=\{x~|~4≤x≤5\}=[4,5]*
- La función *g(x)=\dfrac{1}{x-1}* tiene un dominio implícito que es *D_g=\{x~|~x≠1\}=\mathbb{R}-\{1\},* porque un denominador no puede ser cero.
Es conveniente repasar la notación de intervalos reales y conjuntos para expresar los dominios de funciones.
Rango: es el conjunto de todos los números reales que son imágenes de los elementos del dominio de la función. Se lo denota como *R_f.*
*R_f=\{y\in \mathbb{R}~|~\exist~ x\in D_f\land y=f(x)\}*
Ejemplos:
- La función *f(x)=x^2* tiene por rango *R_f=\{x~|~x≥0\}* porque un número elevado al cuadrado siempre es no negativo.
- La función *g(x)=-3x+5* tiene por rango *R_g=\mathbb{R}* porque la variable dependiente puede tomar el valor de cualquier número real.
Gráficas de funciones escalares
Las funciones reales de variable real pueden representarse gráficamente en un plano donde se ha introducido un sistema de coordenadas cartesianas. El dominio se considera sobre el eje de abscisas (horizontal) y el rango sobre el eje de ordenadas (vertical). Dado que ambos ejes están formados por números reales, el plano se denomina como *\mathbb{R}\times \mathbb{R}* o abreviadamente *\mathbb{R}^2.*
La representación gráfica de una función f está dada por los puntos *(x;y)* del plano para los cuales x está en el dominio de la función e *y=f(x).* Es decir, la gráfica de una función es el conjunto de puntos cuya primera coordenada es un elemento del dominio y la segunda es la imagen correspondiente. La gráfica se denota como *G_f.*
*G_f=\{(x;y)\in \mathbb{R}^2~|~x\in D_f\land y=f(x)\}*
La gráfica nos aporta una idea útil del comportamiento de una función, además, permite comprender conceptos abstractos. Como la coordenada y de cualquier punto de la gráfica es *y=f(x),* podemos leer el valor de *f(x)* directamente desde el gráfico. También, el dominio y el rango de la función pueden extraerse del gráfico.
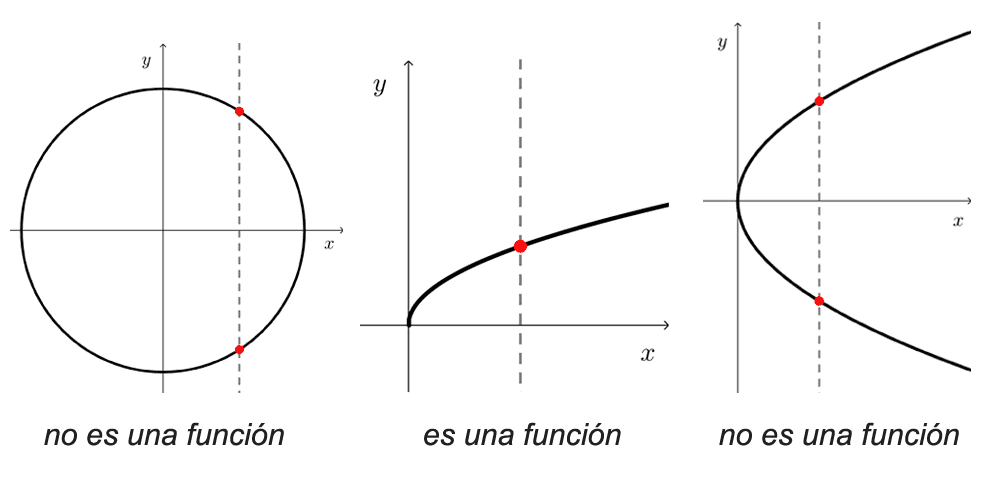
Habitualmente, la gráfica de una función es una curva en el plano cartesiano, pero no todas las curvas del plano son gráficas de funciones. Las gráficas de funciones tienen la propiedad de que una recta vertical puede cortarlas a lo sumo en un punto, pues en caso contrario significa que un mismo número tiene más de una imagen, no cumpliendo con la definición de función.
Este principio se aplica para verificar si una curva es gráfica de una función o no, y se conoce como la prueba de la recta vertical.
Al construir el gráfico de cualquier función es conveniente encontrar, si existen, las intersecciones del mismo con los ejes de coordenadas.
La intersección con el eje y, si existe, es única y se obtiene para *x=0.* Es decir, si existe un punto de intersección de la gráfica con el eje de ordenadas, dicho punto es *(0;f(0)).*
Las intersecciones con el eje x corresponden, si existen, a los puntos donde el valor de la función es cero. Los puntos del dominio donde ocurre esto reciben el nombre de ceros de la función. O sea: el número real *a* es cero de la función si *f(a)=0,* el gráfico de f corta al eje x en el punto *(a;0).*
Según el gráfico, *a_1* y *a_2* son ceros de la función f.
Ejemplos de funciones escalares y sus gráficas
Veremos a continuación algunos ejemplos de funciones reales básicas junto con su representación gráfica.
Funciones lineales
Las funciones lineales son aquellas de la forma *f(x)=mx+b* donde m y b son números reales. El dominio de estas funciones es el conjunto de los números reales, *\mathbb{R}.*
Ejemplos:
*f(x)=x*
*f(x)=2x+1*
Funciones cuadráticas
Las funciones cuadráticas son aquellas de la forma *f(x)=ax^2+bx+c* donde a, b y c son números reales y *a≠0.* El dominio de estas funciones es el conjunto de los números reales, *\mathbb{R}.*
Ejemplos:
*f(x)=x^2*
*g(x)=-x^2+5*
Funciones cúbicas
Las funciones cúbicas son aquellas de la forma *f(x)=ax^3+bx^2+cx+d* donde a, b, c, d son números reales y *a≠0.* El dominio de estas funciones es el conjunto de los números reales, *\mathbb{R}.*
Ejemplos:
*f(x)=x^3*
*f(x)=-x^3+2x^2+1*
Funciones racionales
Las funciones racionales son aquellas de la forma *f(x)=\dfrac{p(x)}{q(x)}* donde p y q son funciones polinómicas, o sea, de la forma:
*p(x)=a_mx^m+a_{m-1}x^{m-1}+...+a_1x+a_0*
*q(x)=b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0*
donde *a_0,a_1,...,a_m~* y *~b_0, b_1,...,b_n* son números reales; *m* y *n* son números naturales.
El dominio de las funciones racionales es el conjunto de todos los números reales excepto aquellos que anulan al denominador *q(x).*
*D_f=\mathbb{R}-\{x~|~q(x)=0\}*
Ejemplos:
*f(x)=\dfrac{1}{x}*
*g(x)=\dfrac{x^2}{1-x}*
Función raíz cuadrada
La función raíz cuadrada es *f(x)=\sqrt{x}.* Su dominio y rango es el conjunto de los reales no negativos.
Función valor absoluto
La función valor absoluto es *f(x)=|x|.* Su dominio es el conjunto de los números reales y su rango es el conjunto de los reales no negativos.
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.






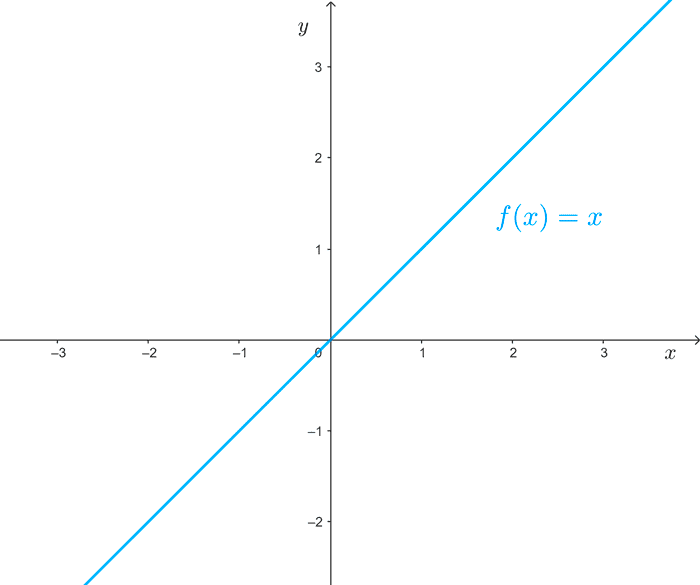







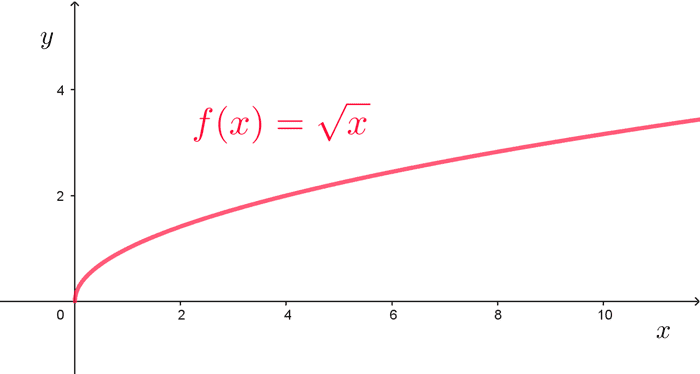

Deja una respuesta