
Límite de una función en un punto
En este artículo se estudia el límite de una función en un punto, se parte explicando el concepto y trabajando con ejemplos de funciones donde el límite existe y otros donde no existe.
Índice
Concepto de límite
En ocasiones nos interesa analizar el comportamiento de los valores de una función, cuando la variable independiente se aproxima a un valor particular. Este estudio nos lleva a definir un nuevo concepto matemático llamado “límite” de la función.
Intuitivamente definimos al límite de una función como el número real al que se aproximan las imágenes (o valores) de una función cuando la variable independiente se aproxima a un número cualquiera, que puede o no estar en el dominio de la función.
Simbólicamente: sea *f* la función, *L* el límite y *a* el valor de la variable independiente. Entonces, cuando *x\to a,* *f(x)\to L* (se lee: “cuando x tiende a a, las imágenes de f tienden a L”). O bien, en una forma más compacta:
$$\lim_ {x\to a} f(x)=L$$
Ejemplos de límites de funciones
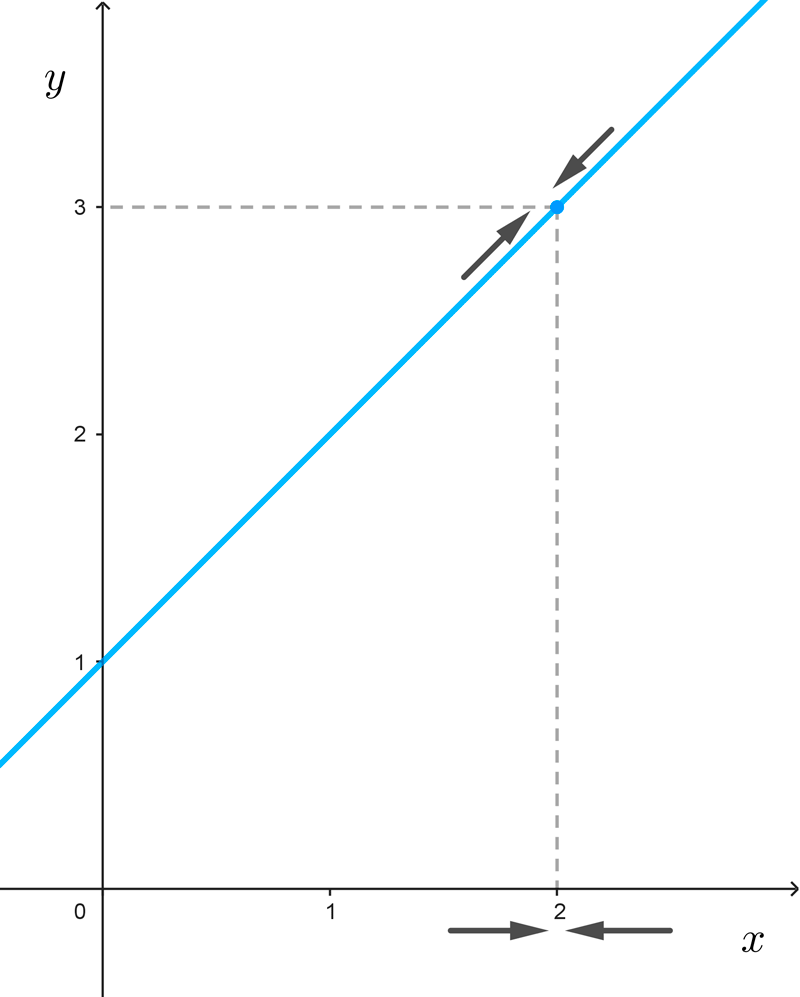
Ejemplo 1: analicemos el comportamiento de la función *f(x)=x+1* cuando x se aproxima al número 2, utilizando una tabla de valores:
| x | 1,8 | 1,9 | 1,99 | 1,999 | 2 | 2,001 | 2,01 | 2,1 | 2,2 |
| f(x) | 2,8 | 2,9 | 2,99 | 2,999 | 3,001 | 3,01 | 3,1 | 3,2 |
Tenemos dos maneras de aproximarnos a 2: por izquierda (tomando valores menores a 2) o por derecha (tomando valores mayores a 2). Podríamos seguir completando la tabla agregando valores cada vez más cercanos a 2, ya sea por izquierda o por derecha, pero el proceso no terminaría nunca porque siempre existirá otro número que se encuentre más cerca.
Sin embargo, la interpretación de la tabla nos lleva a suponer que, por cualquier lado que nos aproximamos a 2, ocurre que los valores de f se acercan a 3. En símbolos, cuando *x\to 2, f(x)\to 3,* que es lo mismo que decir que el límite de la función en 2 es 3:
$$\lim_ {x\to 2} f(x)=\lim_ {x\to 2} (x+1)=3$$
Nótese que no analizamos lo que ocurre con la función en el valor 2. Esto es porque el límite se ocupa de analizar lo que ocurre cuando nos acercamos a un número y no importa qué ocurre particularmente en ese número.
Para poder analizar el límite de f en a, no es necesario que exista f(a), o sea, que la función esté definida en x=a. La imagen de este valor, si existe, es irrelevante. Basta que f(x) esté definida para todos los puntos distintos de a en alguna vecindad de a, esto es, para toda x≠a en un intervalo abierto que contenga a a.
Las aproximaciones por izquierda o por derecha pueden simbolizarse en términos de límites de la siguiente manera:
Límite por la izquierda: corresponde a la aproximación al punto por el lado izquierdo, es decir, con valores menores al que estamos analizando. Se simboliza como: $$\lim_{x\to a^-} f(x)=L$$
Límite por la derecha: corresponde a la aproximación al punto por el lado derecho, es decir, con valores mayores al que estamos analizando. Se simboliza como $$\lim_{x\to a^+} f(x)=L$$
Estos dos se conocen como límites laterales por izquierda y por derecha, respectivamente. En un momento analizaremos su importancia para la obtención del límite.
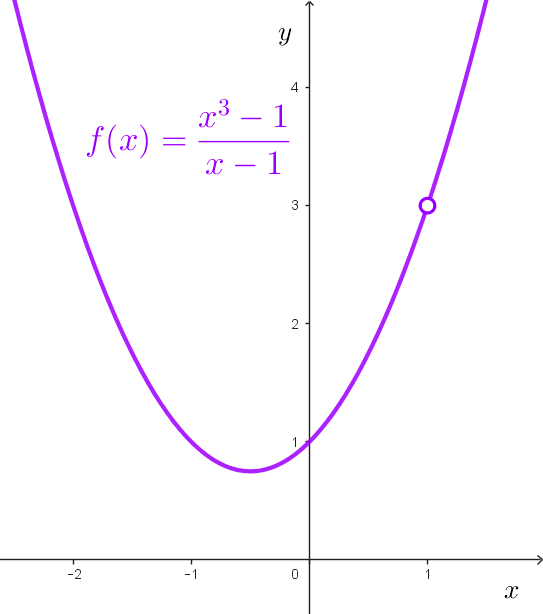
Ejemplo 2: analicemos qué ocurre con la función *f(x)=\dfrac{x^3-1}{x-1}* cuando x se acerca a 1.
Utilizando la simbología que ya conocemos, lo que queremos hallar es el siguiente límite:
$$\lim_{x\to 1} \dfrac{x^3-1}{x-1}$$
Cuando x=1, la función no existe, pues f(1) es el cociente 0/0 el cual no está definido. Sin embargo, la inexistencia de imagen en el punto no es un impedimento para obtener el límite, pues como dijimos, lo que analizamos es qué ocurre cuando nos acercamos a un valor, y la función sí está definida en valores cercanos a 1.
Podemos construir una gráfica de la función, la cual tendrá un “hueco” en x=1.
El análisis de la gráfica nos lleva a suponer que cuando la variable independiente se acerca a 3, las imágenes de la función se acercan a 4. Nos apoyamos de una tabla de valores para intentar confirmar esta suposición:
| x | 0,9 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,1 |
| f(x) | 2,71 | 2,97 | 2,999 | - | 3,003 | 3,03 | 3,31 |
Podemos suponer a partir de esta tabla que cuando nos acercamos a 1 por la izquierda, la función se acerca a 3, o sea, *\lim_{x\to 1^-} \dfrac{x^3-1}{x-1}=3.* Lo mismo pasa cuando nos acercamos a 1 por la derecha: *\lim_{x\to 1^+} \dfrac{x^3-1}{x-1}=3.*
Como las imágenes se acercan a un valor fijo cuando la variable independiente se acerca a 1, podemos decir que el límite existe y es igual a 3.
$$\lim_{x\to 1} \dfrac{x^3-1}{x-1}=3$$
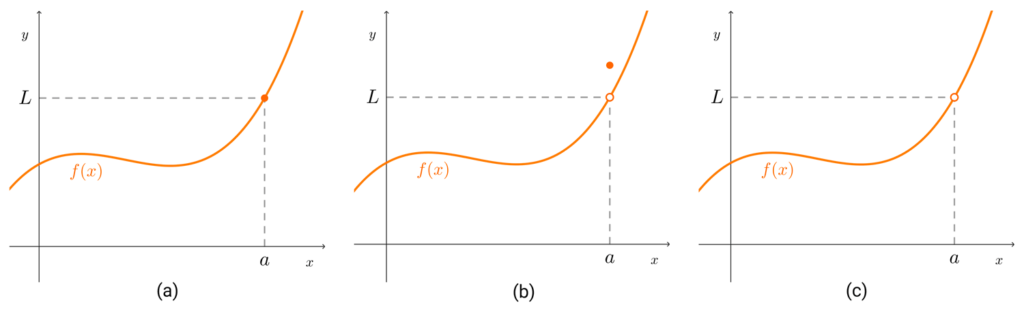
Ejemplo 3: A continuación se presentan las gráficas de tres funciones. Buscamos analizar el límite de cada una en el punto a.
- En la función del ítem a, ocurre que la imagen de a es igual al número L, o sea, *f(a)=L*
- En la función del item b, ocurre que *f(a)≠L.*
- Por último, en la función del item c, ocurre que *f(a)* no existe.
A pesar de que en las tres funciones ocurren cosas distintas en *x=a,* el límite en dicho punto es siempre el mismo, L. O sea, para las tres funciones se cumple que:
$$\lim_{x\to a} f(x)=L$$
Con este ejemplo se busca remarcar lo irrelevante que es conocer el valor de la función en un punto para analizar el límite en dicho punto.
Hasta ahora hemos estimado límites mediante gráficas y tablas. Estos procedimientos producen un valor aproximado del límite. Para funciones simples como las de los ejemplos, esta aproximación es suficiente, pues los números obtenidos como límites son correctos. Sin embargo, para funciones más complejas, debemos desarrollar otras técnicas, las cuales estudiaremos más adelante.
Condición de existencia del límite en un punto
En el ejemplo 1 y 2 nos acercamos al punto de interés por la izquierda y por la derecha, y en ambos casos coincidían los números obtenidos. Esto no es casualidad, pues para que un límite en un punto exista, debe ocurrir que los límites por izquierda y por derecha sean iguales.
Simbólicamente: *\lim_{x\to a} f(x)=L~* si y solo si *~\lim_{x\to a^-} f(x)=L~* y *~\lim_{x\to a^+} f(x)=L*
Límites que no existen
Anteriormente hemos analizado funciones cuyos límites en un punto existen, pero esto no siempre ocurre. A continuación veremos algunos ejemplos donde los límites de las funciones estudiadas no existen.
Ejemplo 1: Analizar si existe el límite de *f(x)=\dfrac{|x|}{x}* cuando *x\to 0.*
Podemos notar que en el punto de interés la función no está definida. Consideremos la gráfica de la función *f(x)=|x|/x.* Puede verse que para valores de x positivos, *|x|/x=1,* mientras que para los valores negativos, *|x|/x=-1.*
Cuando x se aproxima a 0 por la izquierda, las imágenes tienden a -1, mientras que si nos acercamos a 0 por la derecha, las imágenes tienden a 1. O sea:
$$\lim_{x\to 0^-}\dfrac{|x|}{x}=-1$$ $$\lim_{x\to 0^+}\dfrac{|x|}{x}=1$$
No existe un único valor al que se aproxime la función cuando x se aproxima a cero, pues la función tiene un salto en ese punto. Con esto podemos concluir que el límite no existe cuando *x\to 0.* El hecho de que los límites por izquierda y por derecha de un punto no coincidan es suficiente para decir que el límite en el punto no existe.
Ejemplo 2: Encontrar *\lim_{x\to 0} \dfrac{1}{x^2}* si existe.
La función no está definida en el punto de interés. A medida que *x* se acerca a cero, *x^2* también se acerca a 0, y *1/x^2* se hace muy grande. Esto se puede ver en la gráfica de la función y en la siguiente tabla:
| *x* | *\dfrac{1}{x^2}* |
| ±0.5 | 4 |
| ±0.2 | 25 |
| ±0.1 | 100 |
| ±0.01 | 10000 |
| ±0.001 | 1000000 |
Los valores de f(x) no se aproximan a un número fijo sino que crecen sin cota, por esto *\lim_{x\to 0} \dfrac{1}{x^2}* no existe.
Nota: cuando una función tiene el comportamiento de crecer sin cota al acercarse a un valor, se simboliza de la siguiente forma: *\lim_{x\to a} f(x)=\infty.* De modo similar, la función podría decrecer sin cota, alcanzando valores cada vez más negativos, en este caso se escribe *\lim_{x\to a} f(x)=-\infty.* Estas notaciones no están diciendo que el límite exista, pues infinito no es un número real, sino que indican la razón por la que el límite no existe: que la función crece o decrece sin cota.
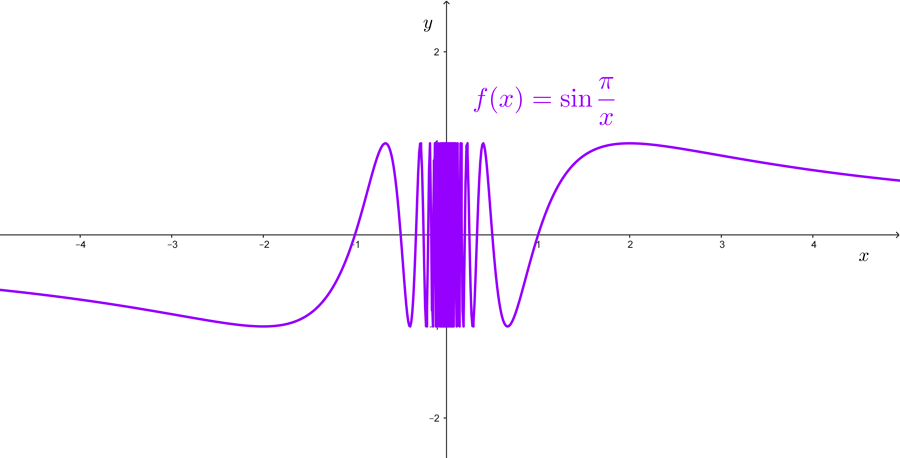
Ejemplo 3: Determinar si existe *\lim_{x\to 0} \sin \left(\dfrac{\pi}{x}\right).*
Otra vez, la función *f(x)=\sin(\pi / x)* no está definida en el punto de análisis. Podemos construir una tabla para ver si las imágenes se aproximan a algún valor.
| x | *\sin(\pi / x)* |
| -0.1 | 0 |
| -0.01 | 0 |
| -0.001 | 0 |
| 0 | - |
| 0.001 | 0 |
| 0.01 | 0 |
| 0.1 | 0 |
Con base a esta información podríamos estar tentados a decir que el límite es igual a cero, pero esto es incorrecto. Si observamos la gráfica de la función, notaremos que al x acercarse a 0, las imágenes oscilan entre -1 y 1.
Debido a que los valores de f(x) no se aproximan a un número fijo cuando x se aproxima a cero, el límite en el punto no existe.
*\lim_{x\to 0} \sin \left(\dfrac{\pi}{x}\right)* no existe.
Comportamientos típicos asociados a la no existencia de un límite
- La función tiende a números diferentes según la variable independiente tienda a un valor por derecha o por la izquierda.
- La función crece o decrece sin cota cuando la variable independiente tiende a un valor.
- La función oscila entre dos números fijos cuando la variable independiente tiende a un valor.
Condición de unicidad del límite
Algunas funciones carecen de límite en un punto, pero aquellas que lo poseen no pueden tener dos límites diferentes en un mismo punto. Es decir, si el límite de una función existe, entonces es único. Simbólicamente:
Si *\lim_{x\to a} f(x)=L_1* y *\lim_{x\to a} f(x)=L_2,* entonces *L_1=L_2*
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.

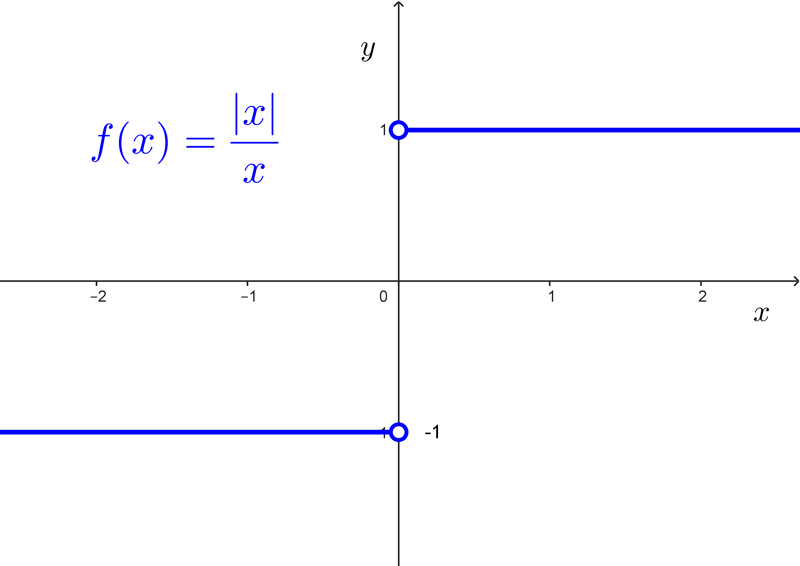



Deja una respuesta