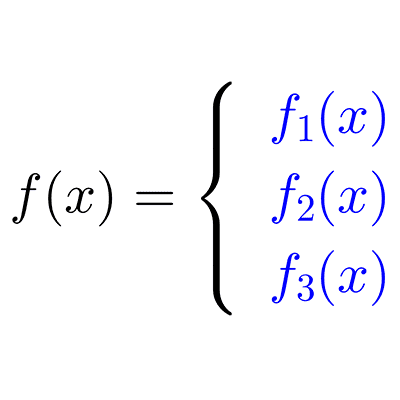
Operaciones con funciones
En este artículo explicamos las operaciones entre funciones, tanto las algebraicas como suma, resta, multiplicación y división, y también la composición de funciones con ejemplos resueltos.
Índice
Suma de funciones
Sean *f* y *g* dos funciones con dominios *D_f* y *D_g* respectivamente.
Función suma de f y g es la función *(f+g)(x)=f(x)+g(x)*
Como f y g deben estar definidas, el dominio de la suma de funciones es el conjunto de valores compartidos por sus dominios, o sea, la intersección de los dominios: $$D_{f+g}=D_f \cap D_g$$
Ejemplo: *f(x)=x+2* y *g(x)= \sqrt{x}*
Los dominios correspondientes son:
*D_f=\mathbb{R}*
*D_g=[0,+∞)*
*(f+g)(x)=f(x)+g(x)=x+2+\sqrt{x}*
*D_{f+g}=D_f \cap D_g =[0,+∞)*
Resta de funciones
Función resta o diferencia de f y g es la función *(f-g)(x)=f(x)-g(x)*
El dominio de la resta de funciones es también el conjunto de valores compartidos por sus dominios: $$D_{f-g}=D_f \cap D_g$$
Ejemplo: *f(x)=x^2+1* y *g(x)=\ln(x+1)* (*\ln* es logaritmo natural)
Los dominios correspondientes son:
*D_f=\mathbb{R}*
*D_{g} =\{x∈\mathbb{R}/x+1>0\}=( -1,+∞)*
*(f-g)(x)=f(x)-g(x)=x^2+1-\ln(x+1)*
*D_{f-g}=D_f \cap D_g=(-1,+∞)*
Producto de funciones
Función producto o multiplicación de f y g es la función *(fg)(x)=f(x)\cdot g(x)*
El dominio de producto de funciones es el conjunto de valores compartidos por sus dominios: $$D_{fg}=D_f \cap D_g$$
Ejemplo: *f(x)=\sqrt{x}* y *g(x)=\sqrt{2-x}*
Los dominios correspondientes son:
*D_f=[0, ∞)*
*D_g=\{x∈\mathbb{R}/2-x≥0\}=(-∞, 2]*
*(fg)(x)=f(x) \ g(x)=\sqrt{x} \ \sqrt{2-x}*
*D_{fg}=D_f \cap D_g=[0,2]*
Cociente de funciones
Función cociente o división de f y g es la función *\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}*
El dominio del cociente de funciones es el conjunto de valores compartidos por sus dominios excluyendo a aquellos que hacen a *g(x)* igual a cero: $$D_{f/g}=D_f \cap D_g-\{x∈\mathbb{R}~|~g(x)=0\}$$
Ejemplo: *f(x)=x^2+6* y *g(x)=x-2*
Los dominios correspondientes son:
*D_f=\mathbb{R}*
*D_g=\mathbb{R}*
*\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}= \dfrac{x^2 +6}{x-2}*
*D_{f/g}=D_f \cap D_g-\{x∈\mathbb{R}~|~x-2=0\}=\mathbb{R}-\{2\}*
Composición de funciones
Composición de las funciones f y g es la función *(f \circ g)(x)=f(g(x))* (se lee "f círculo g", "g compuesta con f", "f de g")
El dominio de la composición de funciones es el conjunto de todos los valores del dominio de g para los cuales g(x) está en el dominio de f: $$D_{f \circ g}=\{x∈\mathbb{R}~|~x∈D_g∧g(x)∈D_f\}$$
La función g tiene dominio Dg y rango Rg, mientras que la función f tiene dominio Df y rango Rf. Nos interesan las imágenes de g que están dentro del dominio de f, pues solo son ellas las que podremos pasar por f. Por esto mismo, solo nos fijaremos en los elementos del dominio de g que devuelvan una imagen contenida en el dominio de f. Si no existen tales elementos, entonces no podremos componer las funciones.
Es necesario para que pueda realizarse la composición que el rango de g esté incluido en el dominio de f, es decir: *R_{g}⊆D_{f}*. Esta es llamada condición de composición.
La función *f \circ g* actúa como un “puente” desde un subconjunto de *D_g* hasta el conjunto *R_f*. Ese subconjunto de *D_g* es precisamente el dominio de la función compuesta. Lo vemos en el siguiente diagrama:
Ejemplo: *f(u)=\sqrt{u}* y *g(x)=2-x*
Debemos asegurarnos antes de todo que se cumpla la condición de composición, es decir, que: *R_{g}⊆D_{f}*. Hallamos ambos conjuntos y vemos que sí se cumple, pues:
*R_g=[0, +∞)* y *D_f=\mathbb{R}*, entonces ocurre que *R_g⊆D_f*.
Para encontrar *f \circ g* primero aplicamos *g* a *x* y luego aplicamos *f* a *g(x)*.
*(f \circ g)(x)=f(g(x))*
*(f \circ g)(x)=f(2-x)*
*(f \circ g)(x)=\sqrt{2-x}*
El dominio de *f \circ g* podemos obtenerlo de la última expresión, pues sabemos que una raíz cuadrada debe tener radicando no negativo (porque la raíz cuadrada de un número negativo no es un número real), entonces:
*D_{f \circ g}=\{x/2-x≥0\}=\{x/x≤2\}=(-\infty, 2]*
Nótese que en este caso *D_{f \circ g}* no es igual al *D_g.*
Preguntas frecuentes
¿Cuáles son las operaciones entre funciones?
Las operaciones básicas entre funciones son la suma, resta, multiplicación y división. Estas operaciones se realizan de manera similar a como se hacen con números, pero aplicadas a funciones.
¿Cómo sumar y restar funciones?
La suma o resta de funciones se realiza sumando o restando los valores correspondientes de las funciones. El dominio es la intersección de los dominios originales.
¿Cómo multiplicar funciones?
La multiplicación de dos funciones se realiza multiplicando los valores correspondientes de las funciones. El dominio de la nueva función es la intersección de los dominios de las funciones originales.
¿Cómo dividir funciones?
La división de dos funciones se realiza dividiendo los valores correspondientes de las funciones. Es importante tener en cuenta que la función denominador no debe ser igual a cero para evitar divisiones indefinidas. El dominio de la nueva función es la intersección de los dominios de las funciones originales excluyendo aquellos valores que anulen el denominador.
