
Teoremas de límites
En este artículo estudiamos teoremas importantes sobre límites que son de utilidad a la hora de calcularlos.
Índice
Teoremas de existencia y unicidad
Existencia del límite: sea *f* una función real y c un punto que puede o no estar en su dominio. El límite de *f* en c existe si y sólo si existen los límites laterales en c y estos son iguales. Simbólicamente:
*\lim_{x\to c} f(x)=L ↔ \lim_{x\to c^+} f(x)=\lim_{x\to c^-} f(x)=L*
Unicidad del límite: si *f* es una función real y existe el límite de *f* en un punto c, entonces este límite es único. Simbólicamente:
*\lim_{x\to c} f(x)=L~~y~~\lim_{x\to c} f(x)=M → L=M*
Límites de las operaciones con funciones
Suponga que k es una constante, n es un entero positivo y que existen los límites *\lim_{x\to a} f(x)* y *\lim_{x\to a} g(x),* entonces se cumplen las siguientes propiedades.
$$\lim_{x\to a} [f(x)+g(x)]=\lim_{x\to a} f(x) + \lim_{x\to a} g(x)$$
$$\lim_{x\to a} [f(x)-g(x)]=\lim_{x\to a} f(x) - \lim_{x\to a} g(x)$$
$$\lim_{x\to a} [k\cdot f(x)]=k\cdot \lim_{x\to a} f(x)$$
$$\lim_{x\to a} [f(x)\cdot g(x)]=\lim_{x\to a} f(x)\cdot \lim_{x\to a} g(x)$$
$$\lim_{x\to a} \dfrac{f(x)}{g(x)}=\dfrac{\lim_{x\to a} f(x)}{\lim_{x\to a} g(x)}~~~(\text{siempre que}~\lim_{x\to a} g(x)≠0)$$
$$\lim_{x\to a} [f(x)]^n=[\lim_{x\to a} f(x)]^n$$
$$\lim_{x\to a} \sqrt[n]{f(x)}=\sqrt[n]{\lim_{x\to a} f(x)}$$
Si n es par, supongamos que *\lim_{x\to a} f(x)>0*
Límites de funciones conocidas
Si *f(x)=k* y a está en su dominio, entonces *\lim_{x\to a} f(x)=\lim_{x\to a} k=k*
Si *f(x)=x* y a está en su dominio, entonces *\lim_{x\to a} x=a*
Si *f(x)=x^n* donde n es un entero positivo y a está en su dominio, entonces *\lim_{x\to a} x^n=a^n*
Si *f(x)=\sqrt[n]{x}* donde n es un entero positivo a está en su dominio, entonces *\lim_{x\to a} \sqrt[n]{x}=\sqrt[n]{a}.* Si n es par suponemos que *a>0*
Límite de una función compuesta: Si f y g dos funciones tales que *\lim_{x\to a} g(x)=L* y *\lim_{x\to L} f(x)=f(L),* entonces $$\lim_{x\to a} f(g(x))=f(\lim_{x\to a} g(x))=f(L)$$
Teorema de la sustitución directa
Si f es una función polinómica, racional o trigonométrica y c está en el dominio de f, entonces:
$$\lim_{x\to c} f(x)=f(c)$$
Este teorema nos dice que el límite de las funciones mencionadas en un punto de su dominio, es igual al valor de la función en ese punto.
Otros teoremas importantes
Teorema: Si *f(x)≤g(x)* cuando x es cercana a c (excepto posiblemente en c) y los límites de *f* y *g* existen cuando x se aproxima a c, entonces:
$$\lim_{x\to c} f(x)≤\lim_{x\to c} g(x)$$
Este teorema nos indica que si los valores de una función f se mantienen por debajo o iguales que los de otra función g cerca de un punto, entonces el límite de f en c también se mantiene por debajo o igual que el límite de g en el mismo punto, si es que ambos límites existen.
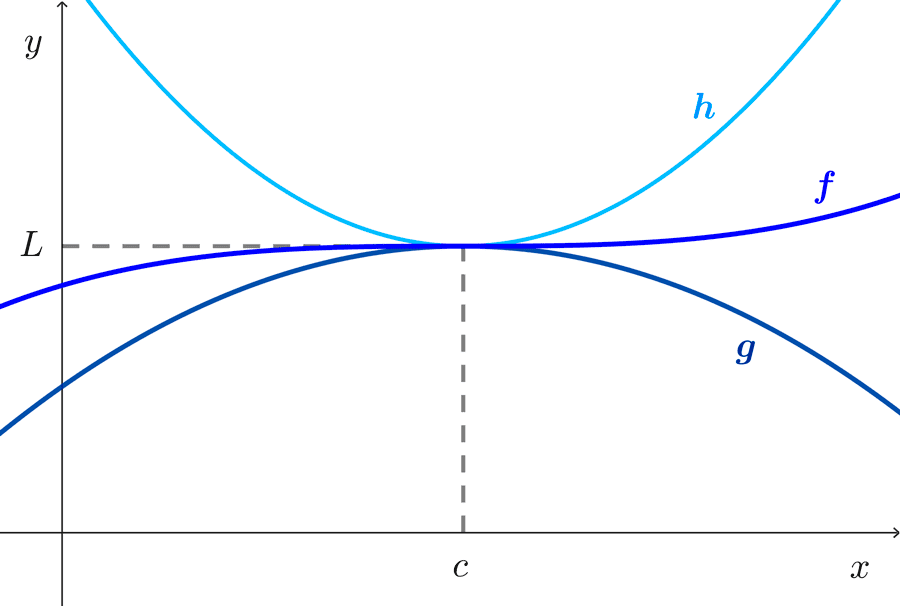
Teorema de compresión (o del sándwich): si *g(x)≤f(x)≤h(x)* cuando x es cercana a c (excepto posiblemente en c) y *\lim_{x\to c} g(x)=\lim_{x\to c} h(x)=L,* entonces:
$$\lim_{x\to c} f(x)=L$$
El teorema de compresión nos dice que si *f(x)* está atrapada entre *g(x)* y *h(x)* cerca de c, y si g y h tienen el mismo límite L en c, entonces f está forzada a tener el mismo límite L en c.
Este teorema resulta útil para calcular gran cantidad de límites, entre ellos el límite trigonométrico fundamental.
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.


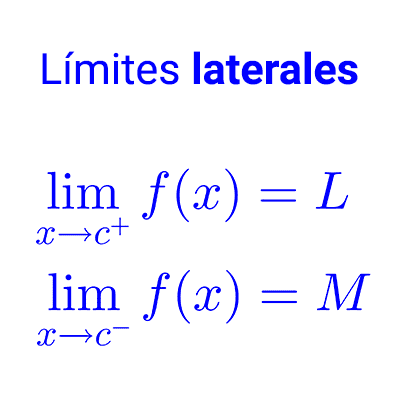


Deja una respuesta