Ecuaciones irracionales
En este artículo explicamos los pasos para resolver ecuaciones irracionales con raíces de cualquier índice (cuadradas, cúbicas, etc.) de forma sencilla y veremos ejercicios resueltos.
Índice
Qué son las ecuaciones irracionales y cómo se resuelven
Una ecuación irracional es una ecuación algebraica donde al menos una incógnita aparece dentro de un radicando, es decir, bajo un signo radical. También son llamadas ecuaciones radicales.
Ejemplo: *\sqrt{x+1}-7=2*
Para hallar la solución, con frecuencia elevamos ambos miembros a un mismo exponente positivo para usar la propiedad cancelativa de las raíces. La nueva ecuación contiene las soluciones de la ecuación original. Sin embargo, en algunos casos la nueva ecuación tiene más soluciones que la ecuación dada. Cualquier solución de la nueva ecuación que no sea una solución de la ecuación dada es llamada una solución extraña, espuria o falsa.
Sabiendo que pueden presentarse soluciones extrañas, es esencial comprobar todas las soluciones obtenidas después de elevar ambos lados de una ecuación a un exponente par. Estas comprobaciones no son necesarias si ambos lados se elevan a un exponente impar, porque en este caso las soluciones falsas no se introducen.
Todo el razonamiento anterior se resume en una serie de pasos para resolver una ecuación irracional:
- Aislar los radicales complejos a un mismo lado de la ecuación.
- Elevar ambos miembros al índice de los radicales (al cuadrado, al cubo, etc.) la cantidad de veces que sean necesarias para remover las raíces.
- Hallar las soluciones de la nueva ecuación.
- Si el exponente a la que se elevó era par, comprobar que todas las soluciones halladas cumplan la ecuación original. Descartar aquellas que no lo hagan.
Ecuaciones con raíces cuadradas
Pasos para resolver una ecuación con raíces cuadradas:
- Aislar los radicales a un mismo lado de la ecuación.
- Elevar ambos miembros al cuadrado la cantidad de veces que sean necesarias para eliminar las raíces.
- Hallar las soluciones de la nueva ecuación.
- Comprobar si todas las soluciones halladas cumplen la ecuación original.
Ejemplo 1 (un radical): *\sqrt{x+1}-7=2*
Es conveniente aislar la raíz cuadrada en el primer miembro sumando *7* a ambos lados:
*\sqrt{x+1}=2+7*
*\sqrt{x+1}=9*
Ahora elevamos al cuadrado ambos lados y, como se eliminó la raíz, la ecuación es de primer grado y se resuelve como es habitual:
*(\sqrt{x+1})^2=9^2*
*x+1=81*
Las solución de esta nueva ecuación es *x=81-1=80*
Comprobamos que esta solución es verdadera reemplazando en la expresión original y verificamos si se cumple la igualdad.
Si *x=80→\sqrt{x+1}-7=\sqrt{80+1}-7=\sqrt{81}-7=9-7=2*
Se cumple la igualdad, por tanto *x=81* es la solución de la ecuación. El conjunto solución es *S=\{81\}*
Ejemplo 2 (un radical): *\sqrt{x-1}=x-7*
Elevamos ambos miembros al cuadrado, para desarrollar será necesario usar la fórmula del cuadrado de un binomio:
*(\sqrt{x-1})^2=(x-7)^2*
*x-1=x^2-14x+49*
*x^2-14x+49-x+1=0*
*x^2-15x+50=0*
Usando la fórmula resolvente para ecuaciones de segundo grado, llegamos a: *x=10* o *x=5*
Comprobación:
Si *x=10:*
*\sqrt{x-1}=\sqrt{10-1}=\sqrt{9}=3*
*x-7=10-7=3*
Los resultados coindiden, por tanto, *x=3* es una solución.
Si *x=5*
*\sqrt{x-1}=\sqrt{5-1}=\sqrt{4}=2*
*x-7=5-7=-2*
Los resultados no coinciden, por tanto, se descarta esta solución. El conjunto solución de la ecuación inicial es *S=\{3\}*
Ejemplo 3 (dos radicales): *\sqrt{3-3x}-\sqrt{3x+2}=0*
*\sqrt{3-3x}=\sqrt{3x+2}*
*(\sqrt{3-3x})^2=(\sqrt{3x+2})^2*
*3-3x=3x+2*
*3-3x-3x-2=0*
*-6x+1=0*
*x=\dfrac{1}{6}*
Comprobación:
Si *x=\dfrac{1}{6}*
*\sqrt{3-3x}-\sqrt{3x+2}=\sqrt{3-3\cdot \dfrac{1}{6}}-\sqrt{3\cdot \dfrac{1}{6}+2}=\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{5}{2}}=0*
La igualdad se cumple, por tanto, *x=\dfrac{1}{6}* es una solución verdadera. *S=\left\{\dfrac{1}{6}\right\}*
Ejemplo 4 (dos radicales): *\sqrt{2x+3}-\sqrt{x+2}=2*
*\sqrt{2x+3}=\sqrt{x+2}+2*
*(\sqrt{2x+3})^2=(\sqrt{x+2}+2)^2*
*2x+3=(\sqrt{x+2})^2+4\sqrt{x+2}+4*
*2x+3=x+2+4\sqrt{x+2}+4*
*2x+3=x+6+4\sqrt{x+2}*
Como la ecuación todavía contiene un radical, se aísla en un lado y de nuevo se elevan al cuadrado ambos lados.
*x-3=4\sqrt{x+2}*
*(x-3)^2=16(x+2)*
*x^2-6x+9=16x+32*
*x^2-22x-23=0*
Las soluciones de esta última ecuación son *x=23* y *x=-1*
Comprobación:
*x=23: \sqrt{2x+3}-\sqrt{x+2}=\sqrt{2(23)+3}-\sqrt{23+2}=\sqrt{49}-\sqrt{25}=7-5=2*
*x=-1: \sqrt{2x+3}-\sqrt{x+2}=\sqrt{2(-1)+3}-\sqrt{-1+2}=\sqrt{1}-\sqrt{1}=1-1=0*
La ecuación tiene solo una solución, *x=23;* la otra solución es extraña. *S=\{23\}*
Los mismos principios se aplican al caso de tener tres o más radicales en la expresión.
Ecuaciones con raíces cúbicas
Pasos para resolver una ecuación con raíces cúbicas:
- Aislar los radicales a un mismo miembro de la ecuación.
- Elevar ambos miembros al cubo la cantidad de veces que sean necesarias para eliminar las raíces.
- Hallar las soluciones de la nueva ecuación.
Nótese que se eliminó el paso de la comprobación. Como dijimos al principio, en los casos de elevar a un exponente impar, no aparecen nuevas soluciones.
Ejemplo 1: *\sqrt[3]{x^2-1}=2*
Elevamos al cubo ambos lados y desarrollamos hasta encontrar la solución.
*(\sqrt[3]{x^2-1})^3=2^3*
*x^2-1=8*
*x^2=9*
*x=±3*
Entonces, las soluciones de la ecuación dada son *3* y *-3.* La comprobación no es necesaria, aunque puede hacerse para detectar errores de cálculo.
Ejemplo 2: *\sqrt[3]{2x+7}-\sqrt[3]{x+1}=0*
*\sqrt[3]{2x+7}=\sqrt[3]{x+1}*
*(\sqrt[3]{2x+7})^3=(\sqrt[3]{x+1})^3*
*2x+7=x+1*
*2x-x=1-7*
*x=-6*
La ecuación tiene entonces una única solución: *-6*
Ecuaciones con raíces de cualquier índice
Cuando los radicales son de índices más altos, se continúa usando el mismo principio que hasta ahora. Es importante siempre comprobar los resultados obtenidos cuando se realizó la elevación a un exponente par.
Si en la ecuación aparecen radicales de diferente índice, es necesario homogeneizarlos, algo que vemos en detalle en la multiplicación de radicales de distinto índice. Si hay fracciones, se procede como en las demás ecuaciones.
Ejemplo 1: *\sqrt[4]{12+2x}=2*
Elevamos a la cuarta ambos miembros y desarrollamos:
*(\sqrt[4]{12+2x})^4=2^4*
*12+2x=16*
*x=2*
Comprobando, la solución *2* es verdadera. *\sqrt[4]{12+2(2)}=\sqrt[4]{16}=2*
Ejemplo 2: *\dfrac{\sqrt[3]{x^2+x}}{\sqrt{(x+1)^3}}=\sqrt{(x+1)^3}*
Se escribe la ecuación de forma conveniente y se multiplican los radicales:
*\sqrt[3]{x^2+x}=\sqrt{(x+1)^3}\cdot \sqrt{(x+1)^3}*
*\sqrt[3]{x^2+x}=\sqrt{(x+1)^6}*
Se escribe la raíz como exponente racional para simplificar más fácil y se llega a que los índices son iguales:
*\sqrt[3]{x^2+x}=(x+1)^{2/6}*
*\sqrt[3]{x^2+x}=(x+1)^{1/3}*
*\sqrt[3]{x^2+x}=\sqrt[3]{x+1}*
Se elevan al cubo ambos miembros y se desarrolla:
*(\sqrt[3]{x^2+x})^3=(\sqrt[3]{x+1})^3*
*x^2+x=x+1*
*x^2=1*
*x=±1*
Al ser un índice impar, no es necesario realizar comprobación.
Bibliografía
- Abálsamo, R., Berio, A., Kotowski, C., Liberto, L., Mastucci, S. y Quirós, N. (2013). Matemática 3. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 4. Puerto de Palos.
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
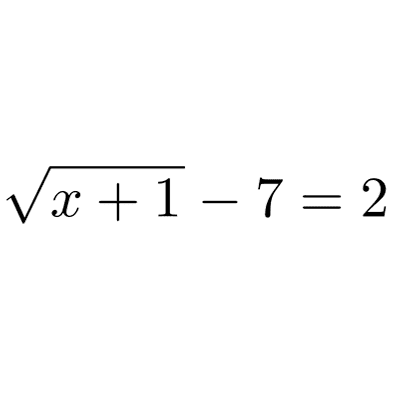
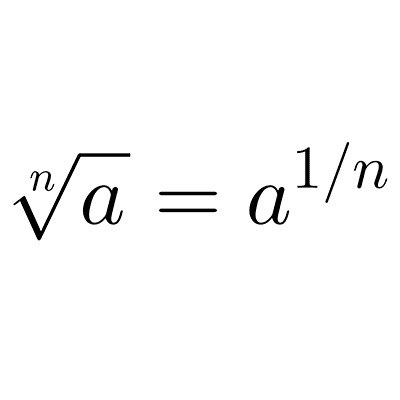




Deja una respuesta