
Límites de funciones trigonométricas
En este artículo exploramos los límites de las funciones trigonométricas en un punto y algunos límites importantes que involucran funciones trigonométricas.
Índice
Límites de funciones trigonométricas básicas
Se ha visto que los límites de muchas funciones algebraicas se pueden calcular por sustitución directa. Cada una de las seis funciones trigonométricas básicas también posee esta deseable propiedad. O sea, el límite de cada función trigonométrica en un punto es igual a la imagen de la función en ese punto.
Límites de funciones trigonométricas
Sea c un número real en el dominio de la función trigonométrica dada. Entonces:
- *\lim_{x\to c} \sin(x)=\sin(c)*
- *\lim_{x\to c} \cos(x)=\cos(c)*
- *\lim_{x\to c} \tan(x)=\tan(c)*
- *\lim_{x\to c} \cot(x)=\cot(c)*
- *\lim_{x\to c} \sec(x)=\sec(c)*
- *\lim_{x\to c} \csc(x)=\csc(c)*
Ejemplos:
*\lim_{x\to 0} \tan x=\tan 0=0*
*\lim_{x\to \pi} (x\cdot \cos x)=(\lim_{x\to \pi}x)(\lim_{x\to \pi}\cos x)=\pi \cdot \cos (\pi)=-\pi*
*\lim_{x\to 0} \sin^2 x=\lim_{x\to 0}(\sin x)^2=0^2=0*
*\lim_{x\to 0} \sin x=0*
*\lim_{x\to 0} \cos x=1*
Los límites de las funciones seno y coseno cuando la variable tiende a infinito o menos infinito no existen, porque ambas funciones son periódicas, variando entre -1 y 1. Las funciones seno y coseno no tienen asíntotas verticales ni horizontales.
- *\lim_{x\to ±\infty} \sin(x)* no existe
- *\lim_{x\to ±\infty} \cos(x)* no existe
Límites trigonométricos importantes
Hay dos límites importantes que involucran al seno y al coseno y sirven para calcular otros límites.
Observe que intentar evaluar directamente el límite *\lim_{x\to 0} \dfrac{\sin(x)}{x}* conduce a una indeterminación 0/0. Sin embargo, se puede demostrar que el valor de este límite es 1. A partir de este límite se puede obtener que *\lim_{x\to 0} \dfrac{1-\cos(x)}{x}=0*
Límites trigonométricos importantes
- *\lim_{x\to 0} \dfrac{\sin(x)}{x}=1*
- *\lim_{x\to 0} \dfrac{1-\cos(x)}{x}=0*
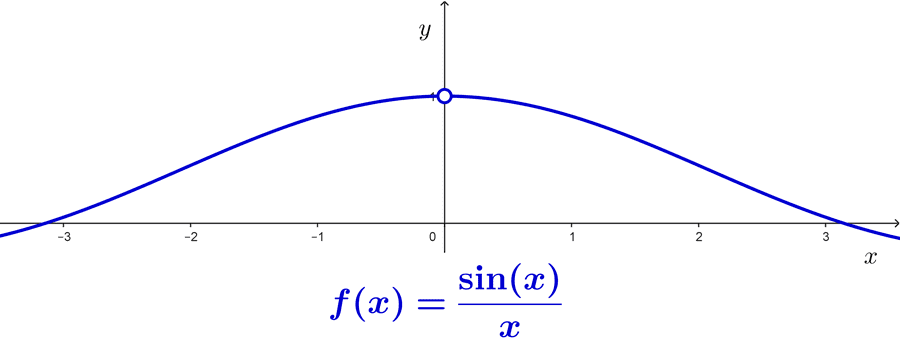

Ejemplo 1: Hallar el límite *\lim_{x\to 0} \dfrac{\tan x}{x}*
Solución: La sustitución directa conduce a la indeterminación 0/0. Para resolver este problema, recurrimos a la identidad trigonométrica *\tan x=\dfrac{\sin x}{\cos x}* y reacomodando la expresión obtenemos:
*\lim_{x\to 0} \dfrac{\tan x}{x}=\lim_{x\to 0} \left(\tan x\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{\cos x}\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{x}\cdot \dfrac{1}{\cos x}\right)*
*=\left(\lim_{x\to 0} \dfrac{\sin x}{x}\right) \left(\lim_{x\to 0}\dfrac{1}{\cos x}\right)*
Como sabemos que *\lim_{x\to 0} \dfrac{\sin x}{x}=1* y *\lim_{x\to 0}\dfrac{1}{\cos x}=1,* podemos obtener:
*\lim_{x\to 0} \dfrac{\tan x}{x}=\left(\lim_{x\to 0} \dfrac{\sin x}{x}\right) \left(\lim_{x\to 0}\dfrac{1}{\cos x}\right)*
*=(1)(1)*
*=1*
Ejemplo 2: Calcular el límite *\lim_{x\to 0} \dfrac{\sin (3x)}{x}*
Solución: la sustitución directa conduce a la indeterminación 0/0. Para solucionar el problema, podemos escribir el límite como:
$$\lim_{x\to 0} \left(\dfrac{\sin (3x)}{x}\cdot \dfrac{3}{3}\right)=3 \left(\lim_{x\to 0} \dfrac{\sin (3x)}{3x}\right)$$
Realizando una sustitución *u=3x* y teniendo en cuenta que *x\to 0* si y solo si *u\to 0,* podemos escribir:
*\lim_{x\to 0} \dfrac{\sin (3x)}{x}=3 \left(\lim_{x\to 0} \dfrac{\sin (3x)}{3x}\right)*
*=3 \left(\lim_{u\to 0} \dfrac{\sin u}{u}\right)*
*=3(1)*
*=3*
Subir








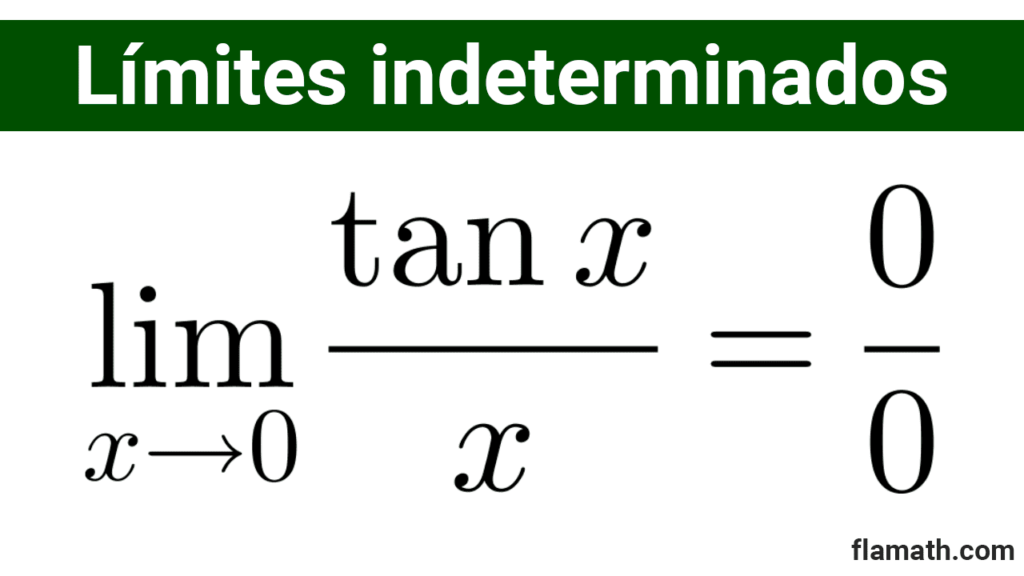
Deja una respuesta