Cómo reducir fracciones a común denominador
En este artículo explicamos cómo hacer una reducción de fracciones a denominador común paso a paso con ejercicios resueltos.
Índice
Cómo hallar un común denominador
Si tenemos dos o más fracciones heterogéneas, la reducción a común denominador consiste en encontrar fracciones equivalentes a las dadas que tengan todas el mismo denominador. De este modo, se facilitan las tareas de sumar, restar, comparar y ordenar fracciones.
El procedimiento que veremos a continuación se conoce como método del mínimo común múltiplo (mcm) y permite hallar fracciones equivalentes que tengan el mínimo común denominador, es decir, de entre todos los posibles, el más pequeño.
Para reducir a común denominador, se realizan los siguientes pasos:
- Calcular el mínimo común múltiplo (MCM) de los denominadores originales. Este valor será el nuevo denominador de las fracciones.
- En cada fracción, dividir el MCM encontrado antes entre cada denominador y el resultado multiplicarlo por el numerador. El valor que resulte de hacer eso será el nuevo numerador de la correspondiente fracción.
Cómo calcular el mínimo común múltiplo de los denominadores
- Descomponer los denominadores en factores primos.
- Elegir los factores comunes y no comunes elevados al mayor exponente.
- Multiplicar los factores, el resultado es el mínimo común múltiplo buscado.
Con la siguiente calculadora podrás obtener rápidamente el Mínimo Común Múltiplo entre dos o más números:
Ejercicios resueltos
1) Reducir las fracciones *\dfrac{3}{5}* y *\dfrac{4}{10}* a común denominador.
En este caso tenemos dos fracciones, hallamos el mínimo común múltiplo entre sus denominadores descomponiendolos primero en factores primos:
*5=5*
*10=5\cdot 2*
Los factores comunes y no comunes son 5 y 2, por tanto el MCM será el producto de ambos.
*MCM(5,10)=5\cdot 2=10*
Este número será el nuevo denominador de las fracciones. Ahora, lo dividimos entre cada numerador y el resultado obtenido lo multiplicamos por el numerador correspondiente.
*10:5=2→\dfrac{3}{5}=\dfrac{3\cdot 2}{10}=\dfrac{6}{10}*
*10:10=1→\dfrac{4}{10}=\dfrac{4\cdot 1}{10}=\dfrac{4}{10}*
Entonces, las fracciones *\dfrac{3}{5}* y *\dfrac{4}{10}* son equivalentes a *\dfrac{6}{10}* y *\dfrac{4}{10}* respectivamente, ambas con el mismo denominador. Esto facilitará la suma, resta y comparación.
2) Reduzca a común denominador las fracciones *\dfrac{1}{2}* y *\dfrac{1}{3}*
Procedemos como lo hicimos en el ejercicio anterior.
*2=2*
*3=3*
*MCM(2,3)=2\cdot 3=6*
*6:2=3→\dfrac{1}{2}=\dfrac{1\cdot 3}{6}=\dfrac{3}{6}*
*6:3=2→\dfrac{1}{3}=\dfrac{1\cdot 2}{6}=\dfrac{2}{6}*
3) Reduce a común denominador las fracciones *\dfrac{3}{25},* *\dfrac{7}{4}* y *\dfrac{11}{40}*
En este caso tenemos que reducir tres fracciones, lo hacemos de la misma forma que hasta ahora.
*25=5^2*
*4=2^2*
*40=2^3\cdot 5*
*MCM(25,4,40)=5^2\cdot 2^3=200*
*200:25=8→\dfrac{3}{25}=\dfrac{3\cdot 8}{200}=\dfrac{24}{200}*
*200:4=50→\dfrac{7}{4}=\dfrac{7\cdot 50}{200}=\dfrac{350}{200}*
*200:40=5→\dfrac{11}{40}=\dfrac{11\cdot 5}{200}=\dfrac{55}{200}*
4) Realizar la reducción a denominador común de las fracciones *\dfrac{3}{x}* y *\dfrac{5}{4}*
Tenemos una x en el denominador de la primera fracción. En la descomposición será necesario expresarlo tal cual.
*x=x*
*4=2^2*
*MCM(4,x)=2^2\cdot x=4x*
*4x:x=4→\dfrac{3}{x}=\dfrac{3\cdot 4}{4x}=\dfrac{12}{4x}*
*4x:4=x→\dfrac{5}{4}=\dfrac{5\cdot x}{4x}=\dfrac{5x}{4x}*
Bibliografía
- Becerril, M., García, P., Grimaldi, V. y Ponce, H. (2017). Matemática en secundaria. Santillana.
- Entre Números I. (2017). Santillana.
- Matemática 1 ESO. (2011). Santillana Educación.
- Matemática 2 ESO. (2012). Santillana Educación.
- Matemática 3 ESO. (2011). Santillana Educación.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.

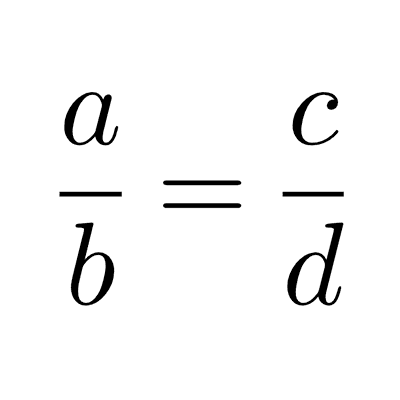




0 - Votos: 0
Subir
Deja una respuesta