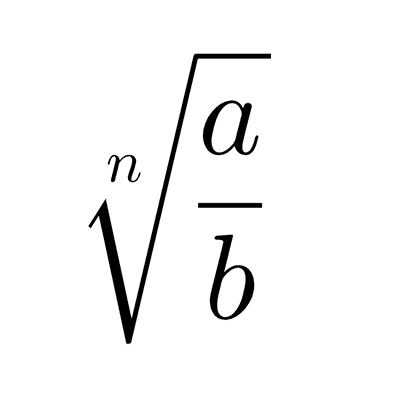
Operaciones combinadas con fracciones

En este artículo explicamos cómo resolver ejercicios combinados con fracciones paso a paso con ejemplos resueltos. Estos cálculos combinados incluyen sumas, restas, multiplicaciones, divisiones, potencias y raíces.

Cómo resolver ejercicios combinados con fracciones

Se debe tener en cuenta que los signos de agrupación como paréntesis, corchetes y llaves indican que dentro de ellos hay un número que no puede ser separado. Por ejemplo, (2+3) ⋅ 5 es diferente de 2+3⋅5, en la primera expresión se indica que el número 2+3 se multiplica a 5, el resultado de esta operación es 25; en la segunda expresión se indica que 2 se suma a la multiplicación de 3 y 5, dando como resultado 17. Esta misma idea se mantiene cuando se presentan fracciones.

Para realizar cálculos combinados con fracciones, es conveniente seguir un orden para la resolución de las operaciones. Esto se conoce habitualmente como una jerarquía en las operaciones y sirve para evitar llegar a resultados incorrectos.

Si hay números mixtos, hay que convertirlos en fracciones antes de realizar el primer paso. Esto se puede hacer sumando la parte entera a la fraccionaria. Por ejemplo: *5~\dfrac{1}{2}=5+\dfrac{1}{2}=\dfrac{11}{2}*

Si hay números escritos en forma decimal, hay que convertirlos en fracciones. Si hay números enteros, conviene escribirlos como fracciones con denominador 1, por ejemplo: *4=\dfrac{4}{1},* esto facilitará el momento de realizar operaciones.

Cálculos combinados con sumas y restas de fracciones

Ejemplo 1

*\left(\dfrac{1}{2}+\dfrac{2}{7}\right)-\dfrac{5}{4}+\dfrac{3}{2}*

Antes de comenzar es importante observar el problema que se presenta. En este caso hay paréntesis que encierran una suma, fuera del paréntesis hay una resta y una suma.

Paso 1: Resolvemos primero lo que está entre paréntesis. En este caso, se sumarán las fracciones que están en rojo.

*{\color{red}\left(\dfrac{1}{2}+\dfrac{2}{7}\right)}-\dfrac{5}{4}+\dfrac{3}{2}*

*=\dfrac{11}{14}-\dfrac{5}{4}+\dfrac{3}{2}*

Nota: Simplificar las fracciones siempre que sea posible facilitará los cálculos y permitirá obtener resultados más manejables.

Paso 2: Ahora resolvemos las sumas y restas que quedan. Simplificamos el resultado final.

*\dfrac{11}{14}-\dfrac{5}{4}+\dfrac{3}{2}*

*=-\dfrac{13}{28}+\dfrac{3}{2}*

*=\dfrac{29}{28}*

Ejemplo 2

*\left(\dfrac{2}{3}+\dfrac{5}{7}\right)+2~\dfrac{1}{3}-\left(\dfrac{5}{17}-\dfrac{14}{8}\right)*

Antes de inciar, convertimos el número mixto en fracción. Este será igual a sumar la parte entera a la fraccionaria: *2~\dfrac{1}{3}=2+\dfrac{1}{3}=\dfrac{7}{3}*. Entonces el ejercicio queda como:

*\left(\dfrac{2}{3}+\dfrac{5}{7}\right)+\dfrac{7}{3}-\left(\dfrac{5}{17}-\dfrac{14}{8}\right)*

Paso 1: Resolvemos los dos paréntesis que aparecen. El resultado queda:

*\dfrac{29}{21}+\dfrac{7}{3}-\left(-\dfrac{99}{68}\right)*

Aplicamos la regla de signos a la última fracción.

*\dfrac{29}{21}+\dfrac{7}{3}+\dfrac{99}{68}*

Paso 2: Calculamos las sumas y restas que quedan.

*\dfrac{26}{7}+\dfrac{99}{68}*

*=\dfrac{2461}{476}*

Ejemplo 3

*\left[\dfrac{2}{3}+1,5-\left(\dfrac{3}{7}-\dfrac{1}{5}\right)+\dfrac{2}{9}\right]-\dfrac{5}{4}*

Antes de comenzar, convertimos el decimal a fracción:

*\left[\dfrac{2}{3}+\dfrac{3}{2}-\left(\dfrac{3}{7}-\dfrac{1}{5}\right)+\dfrac{2}{9}\right]-\dfrac{5}{4}*

Paso 1: Resolvemos primero lo que está entre signos de agrupación, desde adentro hacia afuera. Comenzamos por el paréntesis y luego vamos por los corchetes.

*\left[\dfrac{2}{3}+\dfrac{3}{2}-{\color{green}\left(\dfrac{3}{7}-\dfrac{1}{5}\right)}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\left[\dfrac{2}{3}+\dfrac{3}{2}-\dfrac{8}{35}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\left[\dfrac{13}{6}-\dfrac{8}{35}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\left[\dfrac{407}{210}+\dfrac{2}{9}\right]-\dfrac{5}{4}*

*=\dfrac{1361}{630}-\dfrac{5}{4}*

Paso 2: Ahora que hemos quitado los signos de agrupación, resolvemos la resta que queda:

*\dfrac{1361}{630}-\dfrac{5}{4}=\dfrac{1147}{1260}*

Operaciones combinadas con multiplicaciones y divisiones de fracciones

Ejemplo 1

*\left(\dfrac{7}{8}\cdot \dfrac{2}{5}+\dfrac{3}{5}\right):\dfrac{1}{2}+\dfrac{3}{5}*

Paso 1: Resolvemos primero lo que está entre paréntesis, de izquierda a derecha. Por jerarquía, primero se realizará la multiplicación y luego la suma. Los resultados siempre se simplificarán.

*\left(\dfrac{7}{20}+\dfrac{3}{5}\right):\dfrac{1}{2}+\dfrac{3}{5}*

*=\dfrac{19}{20}:\dfrac{1}{2}+\dfrac{3}{5}*

Paso 2: Ahora resolvemos las multiplicaciones y divisiones, en este caso solo quedó una división.

*\dfrac{19}{20}:\dfrac{1}{2}+\dfrac{3}{5}*

*=\dfrac{19}{10}+\dfrac{3}{5}*

Paso 3: Calculamos la suma.

*\dfrac{19}{10}+\dfrac{3}{5}=\dfrac{5}{2}*

Ejemplo 2

*\left[\dfrac{2}{3}+\left(\dfrac{3}{5}:\dfrac{1}{2}\right)-\dfrac{6}{8}\right]\cdot \dfrac{6}{7}-\left(\dfrac{7}{4}+1\right)*

Paso 1: Resolvemos lo que está entre paréntesis primero. Luego calculamos lo que está entre corchetes.

*\left[\dfrac{2}{3}+\dfrac{6}{5}-\dfrac{6}{8}\right]\cdot \dfrac{6}{7}-\dfrac{11}{4}*

*=\left[\dfrac{28}{15}-\dfrac{6}{8}\right]\cdot \dfrac{6}{7}-\dfrac{11}{4}*

*=\dfrac{67}{60}\cdot \dfrac{6}{7}-\dfrac{11}{4}*

Paso 2: Calculamos la multiplicación que quedó.

*\dfrac{67}{60}\cdot \dfrac{6}{7}-\dfrac{11}{4}*

*=\dfrac{67}{70}-\dfrac{11}{4}*

Paso 3: Calculamos la resta.

*\dfrac{67}{70}-\dfrac{11}{4}=-\dfrac{251}{140}*

Ejemplo 3

*1:\left[\left(\dfrac{3}{5}:\dfrac{1}{2}\right)\cdot \dfrac{5}{6}+3,5\right]+\left(\dfrac{2}{8}:\dfrac{5}{3}-1\right)+5~\dfrac{1}{3}*

Antes de nada, convertimos el decimal y el número mixto en fracciones.

*1:\left[\left(\dfrac{3}{5}:\dfrac{1}{2}\right)\cdot \dfrac{5}{6}+\dfrac{7}{2}\right]+\left(\dfrac{2}{8}:\dfrac{5}{3}-1\right)+\dfrac{16}{3}*

Paso 1: Resolvemos lo que está entre paréntesis primero. Luego calculamos lo que está entre corchetes.

*1:\left[\dfrac{6}{5}\cdot \dfrac{5}{6}+\dfrac{7}{2}\right]+\left(\dfrac{3}{20}-1\right)+\dfrac{16}{3}*

*1:\left[\dfrac{6}{5}\cdot \dfrac{5}{6}+\dfrac{7}{2}\right]-\dfrac{17}{20}+\dfrac{16}{3}*

*1:\left[1+\dfrac{7}{2}\right]-\dfrac{17}{20}+\dfrac{16}{3}*

*1:\dfrac{9}{2}-\dfrac{17}{20}+\dfrac{16}{3}*

Paso 2: Ahora que ya no hay signos de agrupación, calculamos la división.

*1:\dfrac{9}{2}-\dfrac{17}{20}+\dfrac{16}{3}*

*=\dfrac{2}{9}-\dfrac{17}{20}+\dfrac{16}{3}*

Paso 3: Como solo quedan sumas y restas, las calculamos.

*\dfrac{2}{9}-\dfrac{17}{20}+\dfrac{16}{3}*

*=-\dfrac{113}{180}+\dfrac{16}{3}*

*=\dfrac{847}{180}*

Ejemplo 4

*\left[\left(\dfrac{1}{2}-\dfrac{3}{4}\right)+\dfrac{5}{8}:\dfrac{8}{4}\right]\cdot \dfrac{5}{11}*

Aplicamos los pasos de la misma forma que veníamos haciendo.

*\left[-\dfrac{1}{4}+\dfrac{5}{8}:\dfrac{8}{4}\right]\cdot \dfrac{5}{11}*

*=\left[-\dfrac{1}{4}+\dfrac{20}{64}\right]\cdot \dfrac{5}{11}*

*=\dfrac{1}{16}\cdot \dfrac{5}{11}*

*=\dfrac{5}{176}*

Operaciones combinadas con potencias y raíces de fracciones

Ejemplo 1

*\left[\sqrt{\dfrac{1}{2}+\dfrac{1}{16}}+\dfrac{5}{4}\right]^2-1*

Paso 1: Resolvemos primero lo que está dentro de los corchetes. Lo que está dentro de la raíz también cuenta como un paréntesis, así que lo resolvemos.

*\left[\sqrt{\dfrac{9}{16}}+\dfrac{5}{4}\right]^2-1*

*=\left[\dfrac{3}{4}+\dfrac{5}{4}\right]^2-1*

*=2^2-1*

Paso 2: Como hemos eliminado los signos de agrupación, procedemos a hacer la potencia y luego la suma.

*2^2-1=4-1=3*

Ejemplo 2

*\left[\left(\dfrac{1}{2}-\dfrac{1}{6}\right)^3\cdot \sqrt{\dfrac{25}{16}}\right]\cdot \left(\dfrac{1}{5}+\dfrac{7}{15}\right)^2-10\cdot \dfrac{5}{2}*

Paso 1: Resolvemos primero lo que está entre parénteisis, luego lo que está entre corchetes.

*\left[\left(\dfrac{1}{3}\right)^3\cdot \sqrt{\dfrac{25}{16}}\right]\cdot \left(\dfrac{2}{3}\right)^2+\dfrac{157}{243}*

*=\left[\dfrac{1}{27}\cdot \dfrac{5}{4}\right]\cdot \left(\dfrac{2}{3}\right)^2+\dfrac{157}{243}*

*=\dfrac{5}{108}\cdot \left(\dfrac{2}{3}\right)^2+\dfrac{157}{243}*

Paso 2: Ahora resolvemos la potencia.

*\dfrac{5}{108}\cdot \dfrac{4}{9}+\dfrac{157}{243}*

Paso 3: Resolvemos la multiplicación.

*\dfrac{5}{243}+\dfrac{157}{243}*

Paso 4: Ahora podemos resolver la suma.

*\dfrac{5}{243}+\dfrac{157}{243}=\dfrac{2}{3}*

Ejemplo 3

$$(-0,7)^3\cdot \dfrac{10}{21}\cdot 20+\sqrt{0,\overline{4}}:\dfrac{10}{11}-1,0\overline{5}$$

Antes de comenzar, convertimos los enteros y las expresiones decimales en fracciones. El mismo problema reescrito nos queda:

$$\left(-\dfrac{7}{10}\right)^3\cdot \dfrac{10}{21}\cdot \dfrac{20}{1}+\sqrt{\dfrac{4}{9}}:\dfrac{10}{11}-\dfrac{95}{90}$$

Paso 1: Como lo único que está entre paréntesis es una potencia, procedemos a resolver las potencias y raíces.

$$-\dfrac{343}{1000}\cdot \dfrac{10}{21}\cdot \dfrac{20}{1}+\dfrac{2}{3}:\dfrac{10}{11}-\dfrac{95}{90}$$

Paso 2: Resolvemos las multiplicaciones y divisiones de izquierda a derecha.

$$-\dfrac{49}{15}+\dfrac{22}{30}-\dfrac{19}{18}$$

Paso 3: Calculamos la sumas restas de izquierda a derecha y con esto terminamos el problema.

$$-\dfrac{49}{15}+\dfrac{22}{30}-\dfrac{19}{18}=-\dfrac{323}{90}$$

Ejemplo 4

$$\sqrt{\dfrac{25}{16}\cdot \dfrac{36}{4}}-\left(\dfrac{5}{2}+\dfrac{3}{7}-\dfrac{7}{4}\right)$$

Este ejercicio combinado se puede resolver de distintas maneras, veremos dos de ellas.

Primera forma: Aplicando la jerarquía, resolvemos primero lo que está entre paréntesis y dentro de la raíz, luego la raíz y por último las sumas y restas.

$$\sqrt{\dfrac{25}{16}\cdot \dfrac{36}{4}}-\left(\dfrac{5}{2}+\dfrac{3}{7}-\dfrac{7}{4}\right)$$

$$=\sqrt{\dfrac{900}{64}}-\dfrac{33}{28}$$

$$=\dfrac{30}{8}-\dfrac{33}{28}$$

$$=\dfrac{18}{7}$$

Segunda forma: Aplicamos una propiedad de raiz de un producto para distribuir la raíz y la regla de signos para deshacernos del paréntesis.

$$\sqrt{\dfrac{25}{16}\cdot \dfrac{36}{4}}-\left(\dfrac{5}{2}+\dfrac{3}{7}-\dfrac{7}{4}\right)$$

$$=\sqrt{\dfrac{25}{16}}\cdot \sqrt{\dfrac{36}{4}}-\dfrac{5}{2}-\dfrac{3}{7}+\dfrac{7}{4}$$

$$=\dfrac{5}{4}\cdot \dfrac{6}{2}-\dfrac{5}{2}-\dfrac{3}{7}+\dfrac{7}{4}$$

$$=\dfrac{15}{4}-\dfrac{5}{2}-\dfrac{3}{7}+\dfrac{7}{4}$$

$$=\dfrac{18}{7}$$

¡Continúa leyendo estos artículos relacionados!

Cómo reducir fracciones a común denominador

Cómo convertir fracciones en decimales

Radicación de fracciones

Operaciones con fracciones

Cómo ubicar fracciones en la recta numérica