
Propiedades de las fracciones
En este artículo explicamos las propiedades más importantes de las fracciones con ejemplos de cada una. Conocerlas es de gran utilidad a la hora de resolver problemas.
Índice
Propiedades fundamentales de las fracciones
Repasamos a continuación algunas cuestiones básicas sobre los números fraccionarios.
Fracciones equivalentes: Se dice que dos fracciones son equivalentes si representan la misma cantidad, es decir, la misma parte de un entero. Si una fracción *\dfrac{a}{b}* es equivalente a otra *\dfrac{c}{d}*, se puede escribir la igualdad *\dfrac{a}{b}=\dfrac{c}{d}* y se cumple que el producto cruzado es el mismo: *a\cdot d=b\cdot c*
Ejemplos
- *\dfrac{6}{8}=\dfrac{18}{24}* porque *6\cdot 24=8\cdot 18=144*
- *\dfrac{4}{9}=\dfrac{20}{45}* porque *4\cdot 45=9\cdot 20=180*
Simplificación y amplificación: Los números fraccionarios se pueden simplificar o amplificar, es decir, se pueden escribir de diferentes formas equivalentes. Para simplificar una fracción se divide el numerador y el denominador por un mismo factor común. Para amplificar una fracción se multiplica el numerador y el denominador por un mismo factor distinto de cero.
Ejemplos
- Simplificación: *\dfrac{12}{18}=\dfrac{12:2}{18:2}=\dfrac{6}{9}*
- Amplificación: *\dfrac{1}{2}=\dfrac{1\cdot 5}{2\cdot 5}=\dfrac{5}{10}*
Es posible obtener el equivalente irreducible de una fracción, es decir, una fracción que no se puede simplificar más. Para conseguir esto, dividimos el numerador y el denominador entre el máximo común divisor de ambos.
En una fracción, es igual colocar el signo en el numerador, el denominador o delante de la fracción, por ejemplo: *\dfrac{-9}{4}=\dfrac{9}{-4}=-\dfrac{9}{4}*
Los números enteros pueden escribirse como fracción. Para esto, se coloca al entero como numerador y de una fracción con denominador 1. Por ejemplo: *20=\dfrac{20}{1};* *-7=\dfrac{-7}{1};* *14=\dfrac{14}{1};* *0=\dfrac{0}{1}*
Propiedades de la suma
Dadas dos fracciones *\dfrac{a}{b}* y *\dfrac{c}{d},* la suma de ellas se expresa de la siguiente forma:
*\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{ad+bc}{bd}*
La suma de fracciones cumple con las siguientes propiedades.
1) Propiedad conmutativa: El orden en que ubiquemos las fracciones no altera el resultado de la suma.
*\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{c}{d}+\dfrac{a}{b}*
Ejemplo: si tenemos la suma *\dfrac{2}{3}+\dfrac{5}{4}* podemos resolverla tanto de esa forma como cambiando el orden de las fracciones:
*\dfrac{2}{3}+\dfrac{5}{4}=\dfrac{23}{12}*
Cambiando los lugares:
*\dfrac{5}{4}+\dfrac{2}{3}=\dfrac{23}{12}*
Por tanto, *\dfrac{2}{3}+\dfrac{5}{4}=\dfrac{5}{4}+\dfrac{2}{3}*
2) Propiedad asociativa: Es posible agrupar las fracciones de diferentes formas sin cambiar el resultado de la suma.
*\dfrac{a}{b}+\left(\dfrac{c}{d}+\dfrac{e}{f}\right)=\left(\dfrac{a}{b}+\dfrac{c}{d}\right)+\dfrac{e}{f}*
Ejemplo: La suma *\dfrac{1}{2}+\left(\dfrac{1}{6}+\dfrac{4}{3}\right)* se puede reagrupar y el resultado será el mismo.
*\dfrac{1}{2}+\left(\dfrac{1}{6}+\dfrac{4}{3}\right)=2*
*\left(\dfrac{1}{2}+\dfrac{1}{6}\right)+\dfrac{4}{3}=2*
Por tanto:
*\dfrac{1}{2}+\left(\dfrac{1}{6}+\dfrac{4}{3}\right)=\left(\dfrac{1}{2}+\dfrac{1}{6}\right)+\dfrac{4}{3}*
3) Elemento neutro: Existe una fracción que sumada a otra fracción no altera su valor: la fracción cero, *\dfrac{0}{1}.*
*\dfrac{a}{b}+\dfrac{0}{1}=\dfrac{a}{b}*
Ejemplo: *\dfrac{3}{4}+\dfrac{0}{1}=\dfrac{3}{4}*
4) Elemento inverso o simétrico: Para cada fracción existe otra que al sumarse con ella da como resultado la fracción cero. Esta fracción se obtiene cambiando el signo de la original.
*\dfrac{a}{b}+\left(-\dfrac{a}{b}\right)=\dfrac{0}{1}*
Ejemplo: *\dfrac{3}{4}+\left(-\dfrac{3}{4}\right)=\dfrac{0}{1}*
Cuando intervienen fracciones negativas se debe tener cuidado a la hora de aplicar las propiedades.
Ejemplo: *\dfrac{1}{2}-\dfrac{3}{4}=-\dfrac{3}{4}+\dfrac{1}{2}.* La fracción negativa no pierde su signo al usar la propiedad conmutativa, lo mismo ocurre con las demás propiedades.
La resta o diferencia de dos fracciones *\dfrac{a}{b}* y *\dfrac{c}{d}* se puede plantear como la siguiente suma:
*\dfrac{a}{b}-\dfrac{c}{d}=\dfrac{a}{b}+\left(-\dfrac{c}{d}\right)*
Propiedades de la multiplicación
El producto de dos o más fracciones es otra fracción que tiene por numerador el producto de los numeradores, y por denominador al producto de los denominadores.
*\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{a\cdot c}{b\cdot d}*
Si ambas fracciones tienen el mismo signo, el resultado es positivo; si tienen distintos signos, el resultado es negativo. Esto se conoce como la regla de los signos.
Ejemplo: *\dfrac{2}{3}\cdot \dfrac{5}{4}=\dfrac{2\cdot 5}{3\cdot 4}=\dfrac{10}{12}=\dfrac{5}{6}*
La multiplicación de fracciones cumple con las siguientes propiedades.
1) Propiedad conmutativa: el orden de los factores no altera el producto de fracciones.
*\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{c}{d}\cdot \dfrac{a}{b}*
Ejemplo: *\left(-\dfrac{7}{6}\right)\cdot \left(\dfrac{2}{8}\right)=\left(\dfrac{2}{8}\right)\cdot \left(-\dfrac{7}{6}\right)*
*\left(-\dfrac{7}{6}\right)\cdot \left(\dfrac{2}{8}\right)=-\dfrac{7}{24}*
*\left(\dfrac{2}{8}\right)\cdot \left(-\dfrac{7}{6}\right)=-\dfrac{7}{24}*
2) Propiedad asociativa: la forma de agrupar los factores no altera el producto.
*\left(\dfrac{a}{b}\cdot \dfrac{c}{d}\right)\cdot \dfrac{e}{f}=\dfrac{a}{b}\cdot \left(\dfrac{c}{d}\cdot \dfrac{e}{f}\right)*
Ejemplo: *\dfrac{6}{7}\cdot \left(\dfrac{-4}{3}\cdot \dfrac{5}{8}\right)=\left(\dfrac{6}{7}\cdot \dfrac{-4}{3}\right)\cdot \dfrac{5}{8}*
*\dfrac{6}{7}\cdot \left(\dfrac{-4}{3}\cdot \dfrac{5}{8}\right)=-\dfrac{5}{7}*
*\left(\dfrac{6}{7}\cdot \dfrac{-4}{3}\right)\cdot \dfrac{5}{8}=-\dfrac{5}{7}*
3) Propiedad distributiva respecto a la suma y resta: una fracción multiplicada por una suma (o resta) de fracciones es igual a multiplicar la fracción por cada uno de los términos de la suma (o resta).
*\dfrac{a}{b}\cdot \left(\dfrac{c}{d}±\dfrac{e}{f}\right)=\dfrac{a}{b}\cdot \dfrac{c}{d}±\dfrac{a}{b}\cdot \dfrac{e}{f}*
Ejemplo: *-\dfrac{6}{8}\cdot \left(\dfrac{3}{6}+\dfrac{20}{9}\right)=-\dfrac{6}{8}\cdot \dfrac{3}{6}+\dfrac{6}{8}\cdot \dfrac{20}{9}=-\dfrac{49}{24}*
4) Elemento neutro: existe una fracción que multiplicada por cualquier otra fracción no altera su valor: esa fracción es *\dfrac{1}{1}.*
*\dfrac{a}{b}\cdot \dfrac{1}{1}=\dfrac{a}{b}*
Ejemplo: *\dfrac{5}{2}\cdot \dfrac{1}{1}=\dfrac{5}{2}*
5) Elemento inverso o simétrico: para cada fracción existe otra tal que si las multiplicamos da como resultado la fracción *\dfrac{1}{1},* es decir, el elemento neutro. Esta fracción es la inversa y se obtiene de cambiar el orden del numerador y denominador.
*\dfrac{a}{b}\cdot \dfrac{b}{a}=\dfrac{1}{1}*
Ejemplo: *\dfrac{9}{15}\cdot \dfrac{15}{9}=\dfrac{1}{1}*
Propiedades de la división
La división de dos fracciones es una nueva fracción que resulta de multiplicar el dividendo por el inverso del divisor.
*\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a}{b}\cdot \dfrac{d}{c}=\dfrac{a\cdot d}{b\cdot c}*
Una división de una fracción por un número entero se resuelve convirtiendo el entero en una fracción con denominador 1:
*\dfrac{a}{b}:k=\dfrac{a}{b}:\dfrac{k}{1}=\dfrac{a}{bk}*
Una división de un número entero por una fracción se resuelve convirtiendo ese entero en una fracción con denominador 1:
*k:\dfrac{a}{b}=\dfrac{k}{1}:\dfrac{a}{b}=\dfrac{kb}{a}*
Cuando tenemos una fracción sobre otra fracción, podemos aplicar la ley de extremos y medios, también conocida como ley de la oreja o regla del sandwich. Esta ley dice que el resultado de la operación es el producto de los extremos dividido por el producto de los medios. Los extremos son los números superior e inferior, y los medios son los números interiores.
Ejemplo
*\dfrac{\dfrac{3}{4}}{\dfrac{1}{7}}=\dfrac{3\cdot 7}{4\cdot 1}=\dfrac{21}{4}*
La división por sí misma no cumple propiedades especiales.
- No es conmutativa: el orden de los factores sí altera el producto.
- No es asociativa: el resultado puede variar según cómo se agrupen los factores.
Propiedades de la potenciación
La potencia de una fracción resulta de elevar el numerador y el denominador al exponente dado.
*\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}*
Ejemplo: *\left(\dfrac{5}{9}\right)^3=\dfrac{5^3}{9^3}=\dfrac{125}{729}*
Para elevar una fracción a un exponente negativo, se invierte la fracción base y se eleva al exponente cambiado de signo.
*\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}=\dfrac{b^n}{a^n}*
donde *-n* es un número negativo.
Ejemplo: *\left(\dfrac{2}{5}\right)^{-2}=\left(\dfrac{5}{2}\right)^2=\dfrac{5^2}{2^2}=\dfrac{25}{4}*
Exponentes especiales
- Toda fracción elevada a 1 es igual a la misma fracción. *\left(\dfrac{a}{b}\right)^{1}=\dfrac{a}{b}*
- Toda fracción elevada a -1 es igual a la fracción inversa. *\left(\dfrac{a}{b}\right)^{-1}=\left(\dfrac{b}{a}\right)^{1}=\dfrac{b}{a}*
- Toda fracción, distinta de cero, elevada a cero es igual a 1. *\left(\dfrac{a}{b}\right)^{0}=1*
La potenciación de fracciones sigue las mismas reglas que los otros números reales. Si la base es negativa y el exponente es par, el resultado es positivo. Si la base es negativa y el exponente es impar, el resultado es negativo.
Ejemplos
- *\left(-\dfrac{2}{9}\right)^2=+\dfrac{2^2}{9^2}=\dfrac{4}{81}*
- *\left(-\dfrac{1}{2}\right)^5=-\dfrac{1^5}{2^5}=-\dfrac{1}{32}*
Además, se cumplen las propiedades habituales de la potenciación.
Producto de potencias de igual base: para multiplicar dos potencias con la misma base, se conserva la base y se suman los exponentes.
*\left(\dfrac{a}{b}\right)^{m}\cdot \left(\dfrac{a}{b}\right)^{n}=\left(\dfrac{a}{b}\right)^{m+n}*
Ejemplo: *\left(\dfrac{1}{3}\right)^3\cdot \left(\dfrac{1}{3}\right)^6=\left(\dfrac{1}{3}\right)^{3+6}=\left(\dfrac{1}{3}\right)^9*
Cociente de potencias de igual base: para dividir dos potencias de igual base, se conserva la base y los exponentes se restan.
*\left(\dfrac{a}{b}\right)^{m}: \left(\dfrac{a}{b}\right)^{n}=\left(\dfrac{a}{b}\right)^{m-n}*
Ejemplo: *\left(\dfrac{1}{2}\right)^5:\left(\dfrac{1}{2}\right)^3=\left(\dfrac{1}{2}\right)^{5-3}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}*
Potencia de una potencia: al elevar una potencia a un exponente, se conserva la base y se multiplican los exponentes.
*\left[\left(\dfrac{a}{b}\right)^{m}\right]^{n}=\left(\dfrac{a}{b}\right)^{m\cdot n}*
Ejemplo: *\left[\left(\dfrac{2}{3}\right)^3\right]^2=\left(\dfrac{2}{3}\right)^{3\cdot 2}=\left(\dfrac{2}{3}\right)^6*
Potencia de un producto: al elevar una multiplicación a un exponente, se eleva cada factor a dicho exponente.
*\left(\dfrac{a}{b}\cdot \dfrac{c}{d}\right)^{m}=\left(\dfrac{a}{b}\right)^{m}\cdot \left(\dfrac{c}{d}\right)^{m}*
Ejemplo: *\left(\dfrac{5}{7}\cdot \dfrac{2}{9}\right)^2=\left(\dfrac{5}{7}\right)^2\cdot \left(\dfrac{2}{9}\right)^2*
Potencia de un cociente: al elevar un cociente a un exponente, se eleva el dividendo y el divisor a dicho exponente.
*\left(\dfrac{a}{b}: \dfrac{c}{d}\right)^{m}=\left(\dfrac{a}{b}\right)^{m}: \left(\dfrac{c}{d}\right)^{m}*
Ejemplo: *\left(\dfrac{7}{3}:\dfrac{1}{11}\right)^3=\left(\dfrac{7}{3}\right)^2:\left(\dfrac{1}{11}\right)^2*
Propiedades de la radicación
Para obtener la raíz de una fracción, se aplica la raíz al numerador y al denominador.
*\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}*
Las fracciones siguen las mismas reglas que los demás números reales. Por tanto, la raíz de índice par de una fracción negativa no existe, mientras que la raíz de índice impar de una fracción negativa sí existe.
Ejemplos
- *\sqrt{\dfrac{4}{16}}=\dfrac{\sqrt{4}}{\sqrt{16}}=\dfrac{2}{4}=\dfrac{1}{2}*
- *\sqrt[3]{\dfrac{27}{125}}=\dfrac{\sqrt[3]{27}}{\sqrt[3]{125}}=\dfrac{3}{5}*
- *\sqrt{-\dfrac{3}{11}}* no existe.
Suponiendo que las raíces enunciadas existen, la radicación de fracciones cumple con las siguientes propiedades.
Cancelación de raíces
Una raíz y un exponente impares se pueden cancelar si son iguales:
*\sqrt[n]{\left(\dfrac{a}{b}\right)^n}=\dfrac{a}{b}* si *n* es un número impar.
Una raíz y un exponente pares se pueden cancelar si son iguales. Si el radicando es positivo o cero, el resultado es la misma fracción. Si el radicando es negativo, el resultado es la fracción opuesta.
*\sqrt[n]{\left(\dfrac{a}{b}\right)^n}=\dfrac{a}{b}* si *n* es par y *\dfrac{a}{b}* es positivo o cero.
*\sqrt[n]{\left(\dfrac{a}{b}\right)^n}=-\dfrac{a}{b}* si *n* es par y *\dfrac{a}{b}* es negativo.
Ejemplos
*\sqrt[3]{\left(-\dfrac{7}{3}\right)^3}=-\dfrac{7}{3}*
*\sqrt{\left(\dfrac{2}{8}\right)^2}=\dfrac{2}{8}*
*\sqrt[4]{\left(-\dfrac{10}{11}\right)^4}=-\left(-\dfrac{10}{11}\right)=\dfrac{10}{11}*
Raíz de un producto
La raíz de una multiplicación es el producto de las raíces de cada factor, conservando el mismo índice.
*\sqrt[n]{\dfrac{a}{b}\cdot \dfrac{c}{d}}=\sqrt[n]{\dfrac{a}{b}}\cdot \sqrt[n]{\dfrac{c}{d}}*
Ejemplo: *\sqrt{\dfrac{16}{64}\cdot \dfrac{4}{81}}=\sqrt{\dfrac{16}{64}}\cdot \sqrt{\dfrac{4}{81}}*
Se remarca la importancia de que las raíces existan de forma independiente, porque podría darse casos donde la propiedad no es válida, como cuando alguna o ambas fracciones son negativas.
Raíz de un cociente
La raíz de una división es el cociente entre las raíces del dividendo y el divisor.
*\sqrt[n]{\dfrac{a}{b}:\dfrac{c}{d}}=\sqrt[n]{\dfrac{a}{b}}:\sqrt[n]{\dfrac{c}{d}}~~~(b≠0)*
Ejemplo: *\sqrt[3]{\dfrac{3}{5}:\dfrac{7}{9}}=\sqrt[3]{\dfrac{3}{5}}:\sqrt[3]{\dfrac{7}{9}}*
Raíz de una raíz
La raíz de otra raíz es igual a una nueva raíz cuyo índice es la multiplicación de los índices y el radicando se mantiene:
*\sqrt[m]{\sqrt[n]{\dfrac{a}{b}}}=\sqrt[m\cdot n]{\dfrac{a}{b}}*
Ejemplo: *\sqrt[3]{\sqrt[2]{\dfrac{8}{15}}}=\sqrt[3\cdot 2]{\dfrac{8}{15}}=\sqrt[6]{\dfrac{8}{15}}*
Raíz de una potencia
La raíz de una fracción elevada a un exponente es igual a extraer la raíz de la fracción y luego elevarlo al exponente. Sea *a* un número real, *m* y *n* enteros positivos, si *a≥0* cuando *n* es par, entonces:
*\sqrt[n]{\left(\dfrac{a}{b}\right)^m}=\left(\sqrt[n]{\dfrac{a}{b}}\right)^m* siempre que la fracción *\dfrac{a}{b}* sea positiva o cero cuando *n* es par.
Ejemplo: *\sqrt[4]{\left(\dfrac{1}{2}\right)^2}=\left(\sqrt[4]{\dfrac{1}{2}}\right)^2*
Bibliografía
- Becerril, M., García, P., Grimaldi, V. y Ponce, H. (2017). Matemática en secundaria. Santillana.
- Entre Números I. (2017). Santillana.
- Matemática 1 ESO. (2011). Santillana Educación.
- Matemática 2 ESO. (2012). Santillana Educación.
- Matemática 3 ESO. (2011). Santillana Educación.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
2 Comentarios
Deja una respuesta


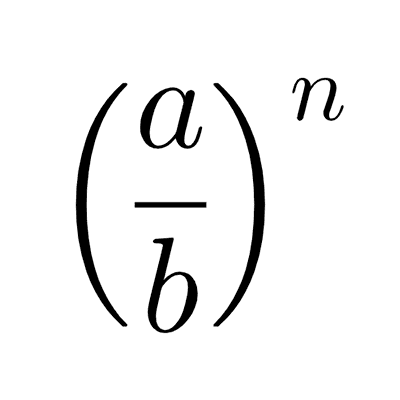
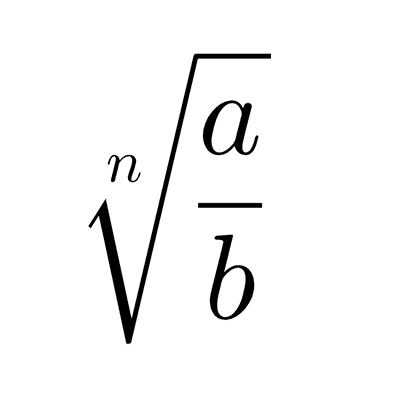





muy bien explicado. gracias