Cómo ordenar fracciones

En este artículo explicamos cómo ordenar fracciones en orden creciente (de menor a mayor) o en orden decreciente (de mayor a menor). Veremos ejercicios resueltos con fracciones de igual o diferente denominador, tanto positivas como negativas.

Índice

¿Cómo ordenar fracciones?

Ordenar fracciones significa colocarlas de forma ascendente (de menor a mayor) o descendente (de mayor a menor). Para lograr esto tenemos dos caminos: analizar directamente la fracción o hallar las expresiones decimales correspondientes y en base a eso ordenarlas. Nos enfocaremos en realizar lo primero.

Los siguientes criterios nos sirven para ordenar fracciones:

Cuando dos fracciones tienen igual denominador, es mayor la fracción que tiene mayor numerador.
Cuando dos fracciones tienen igual numerador, es mayor la fracción que tiene menor denominador.
Una fracción impropia positiva siempre es mayor que una fracción propia positiva.
Una fracción impropia negativa siempre es menor que una fracción propia negativa.
Toda fracción positiva es mayor que una fracción negativa.

Ejercicios resueltos

Fracciones de igual denominador

Para ordenar fracciones con igual denominador de menor a mayor, debemos fijarnos en sus numeradores y ordenarlas desde la que tiene el numerador más bajo hasta la que tiene el numerador más alto.

Para ordenar de mayor a menor, hacemos lo mismo, pero en sentido contrario: desde los numeradores más altos hasta los más bajos. Las fracciones negativas siempre serán menores a las fracciones positivas.

Ejemplo 1: Ordenar de menor a mayor las fracciones *\dfrac{17}{8},* *\dfrac{2}{8}* y *\dfrac{5}{8}.*

Las tres fracciones son homogéneas, por lo cual será menor la que tenga el numerador más pequeño y mayor la del más grande, quedando ordenado así:

*\dfrac{2}{8}<\dfrac{5}{8}<\dfrac{17}{8}*

porque *2<5<17*

También podría haberse deducido que la última es la más grande por ser una fracción impropia y las demás propias.

Ejemplo 2: Ordenar de mayor a menor *-\dfrac{5}{7},* *-\dfrac{8}{7}* y *-\dfrac{27}{7}*

Las fracciones más cercanas a cero serán más grandes que las otras, con eso en mente aplicamos la regla y llegamos a:

*-\dfrac{5}{7}>-\dfrac{8}{7}>-\dfrac{27}{7}*

porque *-5>-8>-27*

Si debemos ordenar fracciones positivas y negativas, hacemos lo correspondiente con cada grupo, recordando que las fracciones negativas siempre son menores que las positivas.

Ejemplo 3: Ordenar de menor a mayor las fracciones *\dfrac{5}{2},* *-\dfrac{5}{2},* *\dfrac{14}{2}* y *-\dfrac{1}{2}*

En el grupo de negativas: *-\dfrac{5}{2}<-\dfrac{1}{2}* porque *-5<-1*

En el grupo de positivas: *\dfrac{5}{2}<\dfrac{14}{2}* porque *5<14*

Juntando la información podemos ordenar todas:

*-\dfrac{5}{2}<-\dfrac{1}{2}<\dfrac{5}{2}<\dfrac{14}{2}*

porque *-5<-1<5<14*

Fracciones de igual numerador

Para ordenar fracciones con igual numerador de menor a mayor, nos fijamos en sus denominadores y las ordenamos desde la que tiene el denominador más alto (que es la fracción más pequeña) hasta la que tiene el denominador más bajo (que es la fracción más grande).

Para ordenar de mayor a menor hacemos lo mismo en sentido contrario: desde la que tiene en denominador más bajo hasta la que tiene el denominador más alto. Las fracciones negativas siempre serán menores a las fracciones positivas.

Esto tiene sentido porque si tomamos la misma cantidad de partes de un entero, tendremos más cuando el entero se haya dividido en menos partes. Por ejemplo: si podemos comer dos porciones de una pizza, comeremos más pizza cuando esta se divida en 4 porciones que cuando se divida en 8.

Ejemplo 1: ordenar de mayor a menor las fracciones *\dfrac{2}{17},* *\dfrac{2}{8}* y *\dfrac{2}{5}.*

En este caso tenemos tres fracciones positivas. Las ordenamos desde el denominador más bajo, que nos da la fracción más alta, hasta el denominador más alto, que nos da la fracción más baja:

*\dfrac{2}{5}>\dfrac{2}{8}>\dfrac{2}{17}*

porque *5<8<17*

Ejemplo 2: ordenar de menor a mayor las fracciones *-\dfrac{2}{17},* *-\dfrac{2}{5}* y *-\dfrac{2}{8}*

Aquí tenemos tres fracciones negativas. Las ordenamos desde el denominador más alto hasta el más bajo recordando que un número negativo es más grande mientras más cerca del cero esté:

*-\dfrac{2}{5}<-\dfrac{2}{8}<-\dfrac{2}{17}*

porque *-5>-8>-17*

Ejemplo 3: ordenar de menor a mayor las fracciones *-\dfrac{5}{6},* *\dfrac{5}{2},* *-\dfrac{5}{3}* y *\dfrac{5}{11}*

En este ejercicio tenemos fracciones positivas y negativas. Como tienen el mismo numerador, ordenamos las negativas y las positivas desde el denominador mayor hasta el denominador menor, cada grupo por separado y luego los juntamos:

*-\dfrac{5}{3}<-\dfrac{5}{6}<\dfrac{5}{11}<\dfrac{5}{2}*

porque *-3>-6* y *11>2* y las fracciones positivas son mayores a las negativas.

Fracciones de distinto numerador y denominador

Para ordenar fracciones que tienen distinto numerador y denominador, debemos encontrar fracciones equivalentes que tengan el mismo denominador y ordenarlas fijándonos en los numeradores como en los casos anteriores.

Para esto se siguen los siguientes pasos:

Hallar el mínimo común múltiplo (MCM) de los denominadores. Este será el nuevo denominador de todas las fracciones.
Dividir el MCM entre cada denominador original y multiplicar el resultado por el numerador. Este será el nuevo numerador de la fracción correspondiente.

Cómo calcular el mínimo común múltiplo de los denominadores

Descomponer los denominadores en factores primos.
Elegir los factores comunes y no comunes elevados al mayor exponente.
Multiplicar los factores, el resultado es el mínimo común múltiplo.

Con la siguiente calculadora podrás obtener rápidamente el Mínimo Común Múltiplo (MCM) entre dos o más números:

Ingrese los números separados por comas:

Mínimo Común Múltiplo:

Ejemplo 1: ordenar de menor a mayor las fracciones: *\dfrac{7}{3},* *\dfrac{21}{10}* y *\dfrac{11}{15}*

Primero descomponemos los denominadores para el mínimo común múltiplo:

*3=3*

*10=5\cdot 2*

*15=3\cdot 5*

*MCM(3,10,15)=3\cdot 5\cdot 2=30*

El denominador nuevo de las fracciones será *30.* Para calcular el numerador de cada fracción dividimos este número entre cada denominador y el resultado lo multiplicamos por el numerador.

Por ejemplo, para *\dfrac{7}{3},* dividimos 30 entre 3:

*30:3=10*

Este resultado lo multiplicamos por 7:

*10\cdot 7=70*

Entonces, el nuevo numerador será 70, quedando *\dfrac{7}{3}=\dfrac{70}{30}*

Para las demás fracciones:

*30:10=3, 3\cdot 21=63.* Entonces *\dfrac{21}{10}=\dfrac{63}{30}*

*\dfrac{11}{15}=\dfrac{11\cdot 2}{30}=\dfrac{22}{30}*

Ahora podemos ordenar porque las fracciones tienen común denominador:

*\dfrac{22}{30}<\dfrac{63}{30}<\dfrac{70}{30}*

porque *22<63<70*

Entonces, reemplazando las fracciones por sus equivalentes originales:

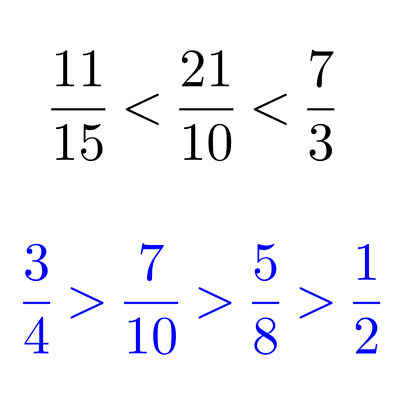
*\dfrac{11}{15}<\dfrac{21}{10}<\dfrac{7}{3}*

Ejemplo 2: ordenar *\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{5}{8}* y *\dfrac{7}{10}* en orden descendente.

Calculamos el MCM de los denominadores:

*2=2*

*4=2^2*

*8=2^3*

*10=5\cdot 2*

*MCM(2,4,8,10)=2^3\cdot 5=40*

Ahora hallamos las fracciones equivalentes a cada una de las originales.

*\dfrac{1}{2}=\dfrac{1\cdot 20}{40}=\dfrac{20}{40}*

*\dfrac{3}{4}=\dfrac{3\cdot 10}{40}=\dfrac{30}{40}*

*\dfrac{5}{8}=\dfrac{5\cdot 5}{40}=\dfrac{25}{40}*

*\dfrac{7}{10}=\dfrac{7\cdot 4}{40}=\dfrac{28}{40}*

Teniendo todas las fracciones con el mismo denominador, podemos ordenarlas de mayor a menor:

*\dfrac{30}{40}>\dfrac{28}{40}>\dfrac{25}{40}>\dfrac{20}{40}*

porque *30>28>25>20*

Reemplazando por las fracciones originales:

*\dfrac{3}{4}>\dfrac{7}{10}>\dfrac{5}{8}>\dfrac{1}{2}*

Preguntas frecuentes

¿Cómo se ordenan fracciones con el mismo denominador?

Para ordenar fracciones con igual denominador de menor a mayor, nos fijamos en sus numeradores y las ordenamos desde la que tiene el numerador más bajo hasta la que tiene el numerador más alto.

¿Cómo se ordenan fracciones con el mismo numerador?

Para ordenar fracciones con igual numerador de menor a mayor, nos fijamos en sus denominadores y las ordenamos desde la que tiene el denominador más alto hasta la que tiene el denominador más bajo.

¿Cómo se ordenan las fracciones con diferente numerador y denominador?

Para ordenar fracciones que tienen distinto numerador y denominador, se deben encontrar fracciones equivalentes que tengan el mismo denominador y ordenarlas en base a los numeradores.