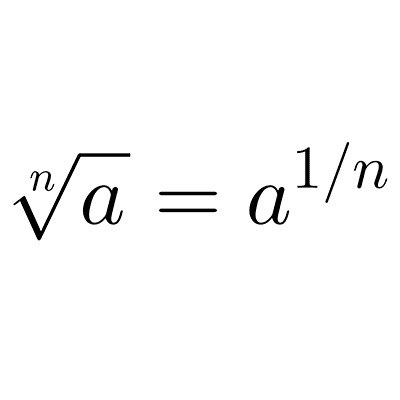
Simplificación de radicales

En este artículo explicamos cómo simplificar radicales con ejercicios resueltos paso a paso. Veremos los casos que pueden darse y qué hacer en cada uno.

¿Qué es un radical simplificado?

Al realizar esta tarea podemos valernos de las leyes de los radicales, las cuales nos permiten simplificar de forma efectiva.

Sean m y n enteros positivos, a y b números reales y todos los siguientes radicales definidos, entonces:

1. *\sqrt[n]{a^n}=a* si n es impar
2. *\sqrt[n]{a^n}=|a|* si n es par
3. *\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}*
4. *\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}*

Como las raíces son una forma de escribir exponentes racionales, la siguiente propiedad también será de utilidad.

Sea m/n un número racional, donde n es un entero positivo mayor que 1. Si a es un número real tal que *\sqrt[n]{a}* existe, entonces:

1. *a^{1/n}=\sqrt[n]{a}*
2. *a^{m/n}=(\sqrt[n]{a})^m=\sqrt[n]{a^m}*
3. *a^{m/n}=(a^{1/n})^m=(a^m)^{1/n}*

Casos de simplificación

Vemos a continuación los distintos casos que pueden darse a la hora de simplificar raíces.

Cancelación de raíces

Si el índice y el exponente de una raíz son iguales, es posible removerlos siguiendo la primera y segunda ley de los radicales. Estas se conocen como raíces perfectas. 

Ejemplos

• *\sqrt{2^2}=2*
• *\sqrt[3]{7^3}=7*
• *\sqrt[7]{6^7}=6*
• *\sqrt[4]{(-2)^4}=|-2|=2*

Un error muy común es simplificar *\sqrt{x^2}* como *x.* Esto solo es válido cuando x es no negativo. Lo mismo ocurre en cualquier raíz con índice par. Lo correcto es realizar el valor absoluto, como en el último ejemplo. Nótese que *\sqrt{(-2)^2}=\sqrt{4}=2,* con lo cual no es correcto simplificar como -2.

Si utilizamos variables en lugar de números, se sigue el mismo principio, siempre teniendo cuidado cuando la raíz es de índice par:

• *\sqrt{y^2}=|y|*
• *\sqrt[3]{w^3}=w*
• *\sqrt[9]{(14x)^9}=14x*
• *\sqrt[4]{(-4x)^4}=|-4x|*

La cancelación tiene sentido también cuando se expresa a los radicales como exponentes. Si a es un número no negativo, entonces:

*\sqrt[n]{a^n}=(a^n)^{1/n}=a^{n/n}=a^1=a*

Extracción de factores del radical

Si el exponente de la raíz es mayor que el índice, es posible extraer algunos factores fuera del radical, incluso a veces eliminar la raíz. 

Por ejemplo, *\sqrt{2^4}* se puede escribir en forma de exponente como *2^{4/2}.* Escribir *4/2* es equivalente a escribir *2,* ya que son el mismo número. Entonces: *\sqrt{2^4}= 2^{4/2}=2^2=4.* Otros ejemplos son:

• *\sqrt[7]{20^{14}}=20^{14/7}=20^2=400*
• *\sqrt[3]{2^{27}}=2^{27/3}=2^9=512*

Se podrían resolver los mismos ejercicios sin necesidad de expresar el radical como exponente, haciendo uso de la siguiente propiedad.

Por esto, el radical *\sqrt[3]{4^9}* se puede simplificar dividiendo el índice y el exponente por el número 3: *\sqrt[3/3]{4^{9/3}}=4^3=64*

En el caso de que el exponente es mayor al índice pero estos no son múltiplos, una técnica consiste en descomponer el radicando en factores cuyos exponentes sean iguales al índice de la raíz.

Por ejemplo, en *\sqrt[3]{2^4},* el radicando *2^4* puede escribirse como *2^3\cdot 2* (por producto de potencias de igual base, el resultado es el mismo). De este modo, haciendo uso de la propiedad de la raíz de un producto:

*\sqrt[3]{2^4}=\sqrt[3]{2^3\cdot 2}=\sqrt[3]{2^3}\sqrt[3]{2}=2\sqrt[3]{2}*

Se ha logrado sacar fuera de la raíz al número 2. Dejando un radical irreducible.

En el caso de raíces cuadradas, los factores deberán tener exponente 2; con raíces cuartas, exponente 4; etc. En ocasiones también será necesario primero descomponer el radicando en factores primos.

Ejemplos

• *\sqrt{7^5}=\sqrt{7^2\cdot 7^2\cdot 7}=\sqrt{7^2}\sqrt{7^2}\sqrt{7}=7\cdot 7\sqrt{7}=49\sqrt{7}*
• *\sqrt[5]{3^{13}}=\sqrt[5]{3^5\cdot 3^5\cdot 3^3}=\sqrt[5]{3^5}\sqrt[5]{3^5}\sqrt[5]{3^3}=3\cdot 3\sqrt[5]{3^3}=9\sqrt[5]{27}*
• *\sqrt{x^6}=\sqrt{x^2\cdot x^2\cdot x^2}=\sqrt{x^2}\cdot \sqrt{x^2}\cdot \sqrt{x^2}=|x|\cdot |x|\cdot |x|=|x^3|*
• *\sqrt{125}=\sqrt{5^3}=\sqrt{5^2\cdot 5}=\sqrt{5^2}\sqrt{5}=5\sqrt{5}*
• *\sqrt{32}=\sqrt{2^5}=\sqrt{2^2\cdot2^2\cdot2}=\sqrt{2^2}\sqrt{2^2}\sqrt{2}=4\sqrt{2}*

Otra técnica consiste en realizar la división entera entre el exponente y el índice. El cociente será el exponente del factor que queda fuera y el resto será el exponente del factor que queda dentro de la raíz. Por ejemplo, en *\sqrt[3]{2^{11}},* realizando la división entera 11÷3, el cociente es 3 y el resto es 2. Por tanto, el exponente del factor que va afuera será 3 y el que queda dentro de la raíz es 2:

*\sqrt[3]{2^{11}}=2^3\sqrt[3]{2^2}=8\sqrt[3]{4}*

Si realizamos la descomposición del radicando y resulta en factores diferentes dentro del radical, hacemos lo que corresponda con cada uno. Si el exponente es igual al índice, se extrae el factor; si el exponente es mayor, se calcula cuántos factores quedarán dentro y cuántos fuera, etc.

Ejemplos

• *\sqrt{40}=\sqrt{2^3\cdot 5}=\sqrt{2^2\cdot 2\cdot 5}=\sqrt{2^2}\sqrt{2\cdot 5}=2\sqrt{10}*
• *\sqrt[3]{432}=\sqrt[3]{3^3\cdot 2^4}=\sqrt[3]{3^3\cdot 2^3\cdot 2}=\sqrt[3]{3^3}\sqrt[3]{2^3}\sqrt[3]{2}=6\sqrt[3]{2}*

Si aparecen variables hay que acordarse de efectuar el valor absoluto en el caso de que la raíz tenga índice par:

• *\sqrt[4]{y^4 x^7}=\sqrt[4]{y^4\cdot x^4\cdot x^3 }=\sqrt[4]{y^4}\cdot \sqrt[4]{x^4}\cdot \sqrt[4]{x^3}=|y||x| \sqrt[4]{x^3}=|xy|\sqrt[4]{x^3}*
• *\sqrt[3]{y^3x^4z}=\sqrt[3]{y^3\cdot x^3\cdot xz}=\sqrt[3]{y^3}\cdot \sqrt[3]{x^3}\cdot \sqrt[3]{xz}=xy\sqrt[3]{xz}*
• *\sqrt[4]{x^6y^3}=\sqrt[4]{x^4\cdot x^2y^3}=\sqrt[4]{x^4}\sqrt[4]{x^2y^3}=|x|\sqrt[4]{x^2y^3}*

Simplificación de índice y exponente

Puede pasar que el índice sea mayor al exponente pero múltiplo de este. En tal caso, se puede recurrir a la forma con exponente para simplificar o dividir índice y exponente por un número conveniente.

Ejemplos

• *\sqrt[4]{3^2}=3^{2/4}=3^{1/2}=\sqrt{2}*
• *\sqrt[6]{x^2}=x^{2/6}=x^{1/3}=\sqrt[3]{x}*
• *\sqrt[20]{16}=\sqrt[20]{2^4}=2^{4/20}=2^{1/5}=\sqrt[5]{2}*

Eliminación de fracciones del radicando

Al principio del artículo vimos que el último criterio para decir que un radical está simplificado es que no existan fracciones en el radicando. Solucionar esta cuestión es sencillo utilizando la ley de raíz de un cociente.

Por ejemplo, *\sqrt{\dfrac{2}{5}}* se puede escribir como *\dfrac{\sqrt{2}}{\sqrt{5}}.* Con esto se eliminan las fracciones del radicando.

Sin embargo, existe una convención que incita a que el denominador de un cociente sea un número racional, es decir, remover los radicales del denominador. Esto se llama racionalizar el denominador.

En nuestro ejemplo podemos hacer esto multiplicando toda la expresión por un cociente igual a uno, situando en el numerador y denominador al radical *\sqrt{5}.*

*\dfrac{\sqrt{2}}{\sqrt{5}}=\dfrac{\sqrt{2}}{\sqrt{5}}\cdot \dfrac{\sqrt{5}}{\sqrt{5}}=\dfrac{\sqrt{2\cdot 5}}{(\sqrt{5})^2}=\dfrac{\sqrt{10}}{5}*

Cómo racionalizar denominadores y numeradores

Es importante asegurarse de que todos los radicales existan de forma independiente. Esto es porque, por ejemplo, *\sqrt{\dfrac{-2}{-7}}* es un número real. Si aplicamos la ley sin cuidado, lo convertimos en *\dfrac{\sqrt{-2}}{\sqrt{-7}},* el cual no es un número real, porque en este campo no existen raíces cuadradas de números negativos.

Preguntas frecuentes

¡Continúa leyendo estos artículos relacionados!

+ Ver infografías