Función inyectiva
En este artículo explicamos qué es una función inyectiva con ejemplos y los métodos para determinar la inyectividad de una función.
Índice
¿Qué es una función inyectiva?
Una función inyectiva es aquella en la que a valores distintos del dominio le corresponden distintas imágenes. En otras palabras, no hay dos elementos diferentes del dominio que tengan la misma imagen. Estas funciones también son llamadas uno a uno.
Formalmente se dice que una función f es inyectiva si y sólo si para cualesquiera a y b en su dominio se cumple que:
*f(a)=f(b)→a=b*
Es decir, si las imágenes de dos valores son iguales, entonces debe ocurrir que esos valores sean iguales.
Una función en la que al menos dos valores del dominio tienen la misma imagen se dice que es no inyectiva. Por ejemplo, la función cuadrática *f(x)=x^2* es no inyectiva porque, por ejemplo, a los valores *x=3* y *x=-3* les corresponde la misma imagen: *f(3)=f(-3)=9.* En cambio, la función cúbica *g(x)=x^3* es inyectiva, pues todo valor de su dominio tiene una imagen diferente a la de los demás.
Geométricamente, si una función es inyectiva, cualquier recta horizontal corta a su gráfica a lo sumo en un punto. Si esto no ocurre, significa que la función toma el mismo valor para al menos dos valores del dominio, con lo cual no es inyectiva.
Existe un teorema que garantiza que las funciones que son crecientes o decrecientes en un intervalo son inyectivas en ese intervalo. Una función que es creciente o decreciente en todo su dominio es inyectiva. Sin embargo, esto es suficiente pero no necesario, una función podría no cumplir esto y aun así ser inyectiva, como es el caso de la función racional *y=1/x.*
La importancia de la inyectividad de una función radica en que es uno de los requisitos para que exista su función inversa, el otro requisito es que sea sobreyectiva. Una función que es inyectiva y sobreyectiva a la vez se llama biyectiva.
En la vida cotidiana podemos pensar en las funciones inyectivas en un salón de clases donde hay alumnos y asientos: cada alumno tiene asignado un asiento específico que ocupa cuando comienza la clase; aquí, la relación entre los alumnos y los asientos puede considerarse como una función inyectiva, porque cada alumno tiene un asiento y un mismo alumno no puede tener más de un asiento asignado.
¿Cómo saber si una función es inyectiva?
Existen dos formas principales para determinar si una función es inyectiva:
- Método algebraico: a partir de la ecuación, determinar las imágenes de dos elementos genéricos del dominio e igualarlas, desarrollando se debe llegar a que los valores del dominio son iguales.
- Método gráfico: si disponemos de la gráfica de la función en el plano cartesiano, podemos realizar varios trazos de rectas horizontales y comprobar si éstas cortan en más de un punto a la gráfica. Esta técnica es conocida como prueba de la recta horizontal.
Para probar que una función no es inyectiva basta con encontrar dos valores diferentes del dominio que tengan la misma imagen o al menos una recta horizontal que corte a la gráfica en más de un punto.
Método algebraico
Como dijimos, este método consiste en encontrar las imágenes de dos valores genéricos del dominio e igualarlas, desarrollando la expresión se tiene que llegar a que los valores del dominio son iguales. Esta técnica parte de la definición de inyectividad: *f(a)=f(b)→a=b.*
Ejemplo 1: determinar si la función cuadrática *f(x)=x^2+1* es inyectiva.
Solución: comenzamos hallando las imágenes de dos elementos del dominio, a y b.
*f(a)=a^2+1*
*f(b)=b^2+1*
Igualamos las expresiones y desarrollamos:
*f(a)=f(b)*
*a^2+1=b^2+1*
*a^2=b^2*
*\sqrt{a^2}=\sqrt{b^2}*
*|a|=|b|*
*a=±b* (propiedad del valor absoluto)
Llegamos a la conclusión de que *a=b* o *a=-b* cuando deberíamos haber llegado a que *a=b.* Por esta razón, la función no es inyectiva.
Ejemplo 2: probar si la función lineal *g(x)=3x+2* es inyectiva.
Solución: hacemos lo mismo que en el ejemplo anterior.
*g(a)=3a+2*
*g(b)=3b+2*
*g(a)=g(b)*
*3a+2=3b+2*
*3a=3b*
*a=b*
Se llegó a la igualdad *a=b,* esto quiere decir que partiendo de imágenes iguales se llega a que las preimágenes (a y b) también son iguales. Por tanto, la función es inyectiva.
Método gráfico
Prueba de la recta horizontal: una función es inyectiva si y sólo si ninguna recta horizontal corta a su gráfica en más de un punto.
Ejemplo 1: determinar si la función *h(x)=2x+1* es inyectiva.
Solución: teniendo la gráfica de la función, trazamos algunas rectas horizontales y verificamos que, si alguna corta a la gráfica, lo haga en un solo punto.
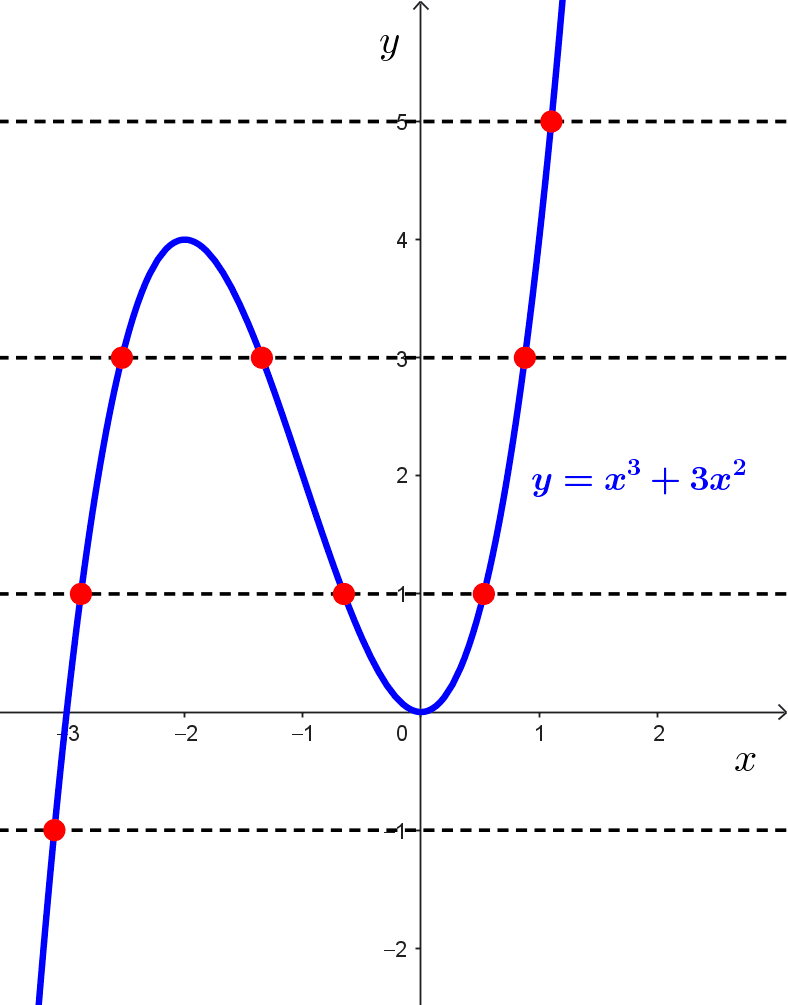
Ejemplo 2: probar si la función cúbica *y=x^3+3x^2* es inyectiva.
Solución: a partir de la gráfica, realizamos el mismo procedimiento que antes dibujado líneas horizontales.
Nota: no se debe confundir la prueba de la recta horizontal con la prueba de la recta vertical, la cual es para determinar si una curva del plano cartesiano es una función o no.
Restricciones de dominio
Restringir el dominio de una función a un intervalo específico puede hacer que una función que no era inyectiva pase a serlo.
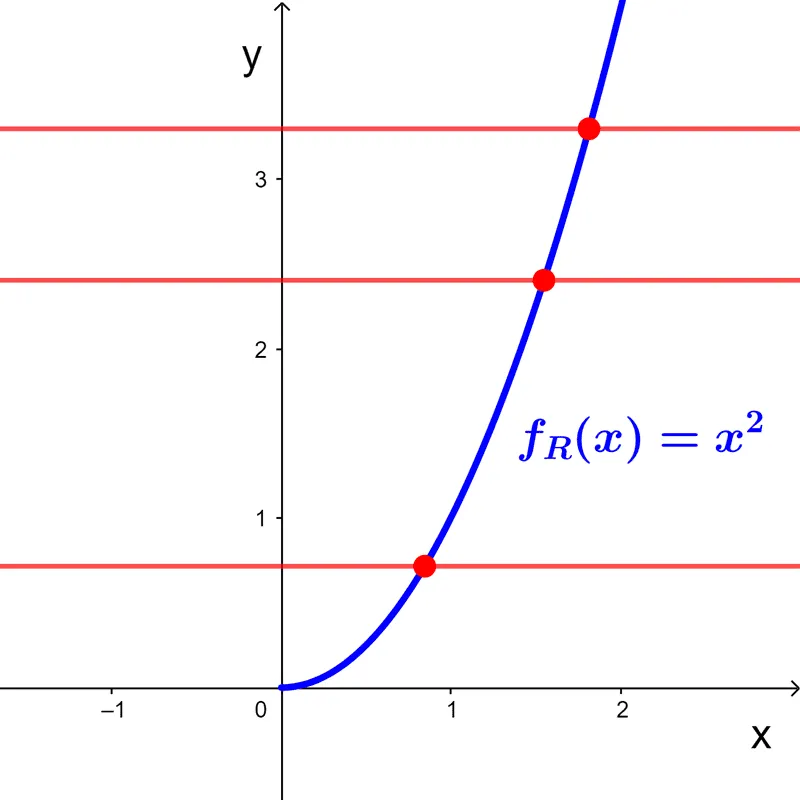
Por ejemplo, al comienzo vimos que la función cuadrática *f(x)=x^2* no era inyectiva si consideramos que su dominio es *\mathbb{R}.* Sin embargo, si consideramos como dominio al conjunto de los reales no negativos, es decir, al intervalo *[0,+∞),* la función pasa a ser inyectiva. En efecto, si llamamos *f_R* a la función con dominio restringido, su gráfica pasa la prueba de la recta horizontal.
Para determinar las restricciones adecuadas que convierten una función en inyectiva, es necesario analizar cuidadosamente su comportamiento en el dominio original. Se deben identificar los puntos problemáticos donde dos o más valores del dominio tienen la misma imagen y asegurarse de que eso no ocurra en el nuevo dominio.
Ejemplos
Las siguientes afirmaciones pueden ser de utilidad a la hora de determinar la inyectividad de una función:
- Todas las funciones lineales no constantes son inyectivas.
- Las funciones constantes no son inyectivas.
- Las funciones potenciales de la forma *y=x^n,* donde n es un entero positivo, son inyectivas cuando n es impar y no son inyectivas cuando n es par.
- Las funciones exponenciales y logarítmicas son inyectivas.
- Las funciones radicales de la forma *y=\sqrt[n]{x},* donde n es un entero positivo, son inyectivas.
- Las funciones trigonométricas seno, coseno y tangente no son inyectivas en sus dominios naturales, pero es posible realizar restricciones de dominio para que sean inyectivas.
Ejemplos de funciones inyectivas:
- *y=x-1*
- *y=x^5+3*
- *y=\dfrac{1}{x}*
- *y=\sqrt{x+1}*
- *y=\ln(x)*
Ejemplos de funciones no inyectivas:
- *y=3x^2+4*
- *y=|x|*
- *y=3x^3+5x^2*
- *y=-5*
- *y=\cos(x)*
Ejemplos de funciones inyectivas pero no sobreyectivas:
- *y=\sqrt{x}*
- *y=e^x*
- *y=\dfrac{1}{x}*
- *y=x^2,* *x≥0*
- *y=\sqrt[4]{x}*
Preguntas frecuentes
¿Cuál es la diferencia entre una función inyectiva y una función sobreyectiva?
La diferencia entre una función inyectiva y una sobreyectiva radica en su relación con los elementos del dominio y del codominio. Una función inyectiva asigna elementos distintos del dominio a elementos distintos del codominio, mientras que una función sobreyectiva cubre todo el codominio, es decir, para cada elemento del codominio existe al menos un elemento del dominio que es su preimagen.
¿Cuál es la diferencia entre una función inyectiva y una función biyectiva?
La diferencia entre una función inyectiva y una función biyectiva es que una función inyectiva asigna cada elemento del dominio a un único elemento del codominio, mientras que una función biyectiva es tanto inyectiva como sobreyectiva, lo que significa que cada elemento del dominio se asigna a un único elemento del codominio y que todo elemento del codominio es alcanzado por al menos un elemento del dominio. Toda función biyectiva es inyectiva pero no toda inyectiva es biyectiva.